تويت
حساب قضايا
_ - _
حساب القضايا
القضايا وجداول الحقيقة
قيمة الحقيقة هي إما 1 (أي صحيحة) أو 0 (أي خاطئة)، والقضية (في اللغة) هي جملة ذات معنى بحيث تكون لها قيمة حقيقة معينة تماماً، ومتغير قضية هو متغير رياضي (منطقي) يمثّل قضية، ويرمز له بالرمز p أو q أو r، والربط المنطقي هو عملية (منطقية) تستعمل لبناء قضايا جديدة انطلاقاً من قضايا معطاة، حيث تكون قيم الحقيقة للقضايا الجديدة مرتبطة بقيم الحقيقة للقضايا المعطاة.
يقال عن قضية إنها مركبة إذا كانت محوّرة عن قضية أخرى، أو كانت مؤلفة من أكثر من قضية واحدة، أي إذا كانت تحوي ربطاً منطقياً واحداً على الأقل. ويقال عن قضية إنها بسيطة إذا لم تكن مركبة.وتمثَّل القضية البسيطة، عادةً، بمتغيّر منطقي واحد.
جدول الحقيقة هو ذلك الجدول الذي يصف الدستور المعيّن لأجل عملية منطقية، أي: من أجل كل توفيق من قيم الحقيقة للقضايا البسيطة، التي تتألف منها العبارة المدروسة والمشكّلة بوساطة العملية، فإن الجدول يعطي قيمة الحقيقة للعبارة المذكورة.
يعرّف الربط الأحادي المسمى (النفي) والذي يرمز له بالرمز ~ بوساطة جدول الحقيقة الآتي:
ويعرّف الربط الثنائي المسمى [الوصل (و)] والذي يرمز له بالرمز Λ بوساطة الجدول الآتي:
ويعرّف الربط الثنائي المسمى [الفصل (أو)] والذي يرمز له بالرمزÚ بوساطة الجدول الآتي:
ويعرّف الربط الثنائي المسمى [الشَّرطي] والذي يرمز له بالرمز → بوساطة الجدول الآتي:
ويعرّف الربط الثنائي المسمى [ثنائي الشَّرطية] والذي يرمز له بالرمز ↔ بوساطة الجدول الآتي:
يمكن ذكر عمليات منطقية أخرى لها تسمياتها الخاصة ورموزها الخاصة ويمثل كل منها ربطاً ثنائياً معرفاً بوساطة الجدول الآتي:
إن القضية p → q تعني أية واحدة من الجمل الآتية:
(1): إذا p فإن q.
(2): p شرط كاف لـ q.
(3): q شرط لازم لـ p.
(4): p تقتضي q.
وإن القضية p ↔ q تعني أية واحدة من الجمل الآتية:
(1): p إذا وفقط إذا q.
(2): كل من p,q تقتضي الأخرى.
(3): p شرط لازم وكاف لـ q.
(4): q,p متكافئتان.
وإن عدد القضايا المنطقية غير المتكافئة والتي تتبع لمتغيرين هو (16) لأنَّ كلاً من الأسطر الأربعة في جدول الحقيقة له إمكانيتان. فعلى سبيل المثال:
وفي الحالة العامة فإن عدد القضايا المنطقية الممكنة المختلفة هو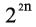 
عندما يكون عدد المتغيرات مساوياً n، وذلك لأنه يوجد 
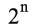سطراً في جدول الحقيقة حينئذ.
ملاحظات وأمثلة:
1 - إن للأقواس في القضايا دوراً أساسياً ومهماً فهي توضح عبارة القضية وتبيّن ترتيب العمل لكتابة جدول الحقيقة لها وتزيل أيّ التباس.
ويظهر ذلك في الجدول الآتي للقضية (pÚq) → (~p Λ ~q):
2 ـ إذا كانت القضية تتبع لمتغيرات،عددها n، فإن جدول الحقيقة لها يتكوّن من 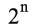سطراً فمثلاً، يمكن ملاحظة أن جدول القضية (pÚ q) → (rÚ~p) ، حيث n = 3، هو الآتي:
3 ـ قد تُستعمل لبعض العمليات المنطقية رموز أخرى غير المستخدمة هنا.
المصدوقات، الاقتضاء، التكافؤ
المصدوقة هي قضية صحيحة دوماً، أي أن قيمة الحقيقة لها هي 1 وذلك أياً كانت قيم الحقيقة للقضايا البسيطة التي تدخل في تكوينها.
فالقضية p → (p∨q) مصدوقة بملاحظة الجدول الآتي:
والخُلف هو قضية خاطئة دوماً،أي أن قيمة الحقيقة لها هي (0) وذلك أياً كانت قيم الحقيقة للقضايا البسيطة التي تدخل في تكوينها.
فالقضية ~ (~q → (p Ú~p)) خُلف بملاحظة الجدول الآتي:
والقضية ~q → (q Λ p) ليست مصدوقة وليست خلفاً.
والقضية (pÚq) ↔ (q Úp) مصدوقة.
وإذا رُمز للمصدوقة بالرمز t وللخُلف بالرمز c فإن:القضية ~t تكون خُلفاً، والقضية ~c تكون مصدوقة.
والقضية pÚ~p مصدوقة، والقضية p Λ ~p خُلف.
وإذا كانت القضية f (p, q,….), مصدوقة فإنّ f (f1, f2,….), تكون مصدوقة لأجل أية قضاياf1, f2,…. فمثلاً، إذا أُخذت المصدوقة (p Λ q) ↔ (q Λ p) وتمّ التعويض فيها q Λ r بـ p وp بـ q فإن القضية الناتجة: (q Λ r) Λ p↔p Λ (q Λ r) تكون مصدوقة.
يقال إنّ قضية مثل P تقتضي قضية مثل Q، ويستعمل الرمز P ⇒ Q للتعبير عن ذلك، إذا كانت Q صحيحة كلما كانت P صحيحة. ويقال، في هذه الحالة، إنّ P أقوى من Q، وإنّ Q أضعف من P.
الاقتضاء، ورمزه ⇒، يحدّد علاقة بين قضيتين، فمثلاً P ⇒ Q، يُحدّد علاقة تؤكد أن القضية P ↔ Q مصدوقة.
يقال إن قضية P تكافئ قضية Q، ويستعمل الرمز P ⇔ Q للتعبير عن ذلك، إذا كانت لهما قيم الحقيقة ذاتها أياً كانت قيم الحقيقة لمتغيراتهما. ويقال، في هذه الحالة، إن هاتين القضيتين متطابقتان ويستخدم، للتعبير عن ذلك، الرمز P ≡ Q
التكافؤ، ⇔ أو ≡، يحدد علاقة بين قضيتين، فمثلاً P ⇔ Q، يحدد علاقة تؤكد أن القضية P → Q مصدوقة.
ملاحظات ونتائج وأمثلة مهمة:
أ ـ من الممكن أن لا تكون القضية p → q مصدوقة أو خُلفاً.
ب ـ من الممكن أن لا تكون القضية p ↔ q مصدوقة أو خُلفاً.
جـ ـ أياً كانت القضايا P, Q, R فإنّ:
(1) P ⇔ p, P ⇒ p.
(2) إذا كان P ⇒ Q, Q ⇒ R فإن p ⇒ R. وأيضاً، إذا كان P ⇔ Q, Q ⇔ R فإنّ p ⇔ R.
(3) إذا كان P ⇒ Q, Q ⇒ P فإن P ≡ Q، لأنّ: [P ⇔ Q إذا وفقط إذا P ⇒ Q, Q ⇒ P].
(4) إذا كان P ⇔ Q فإنّ Q ⇔ P.
د - العلاقة ⇔ تكون علاقة تكافؤ على أية مجموعة من القضايا.
هـ - العلاقة ⇒ تكون علاقة ترتيب (جزئي) على أية مجموعة من القضايا.
و P ⇔ Q- إذا وفقط إذا P↔ Q مصدوقة.
ز - يمكن استخدام جدول الحقيقة للبرهان على تطابق قضيتين.
ح - إذا وجد متغير واحد على الأقل داخلاً في عبارة إحدى قضيتين متطابقتين ولتكن الأولى (مثلاً) وغير داخل في عبارة الثانية فهذا يعني أن قيمة الحقيقة للقضية الثانية مستقلة عن قيم الحقيقة لهذه المتغيرات غير الداخلة فيها. ادرس المثال:
(p Úq) ≡ ((rÚ~r) → (pÚq))
ط - إنّ (p → q) ≡ (~ p Ú q) بملاحظة الجدول الآتي:
ي - يمكن الاكتفاء بالعمليات الثلاث Λ ،Ú، ~للتعبير عن العمليات الخمس ↔, →, Λ، Ú,~ . ولبرهان هذا يكفي ملاحظة التطابقين:
(p → q) ≡ (~p Ú q)
(p ↔ q) ≡ ((p → q) Λ (q → p))
وإضافة إلى ذلك، يمكن الاكتفاء بالعمليتين Λ, ~ أو بالعمليتين Ú, ~ بملاحظة المطابقات:
~ (p Ú q) ≡ ~ p Λ ~q
~ (p Λ q) ≡ ~ pÚ ~q
~ (~p) ≡ p
وبالتالي:
(p ∨ q) ≡ ~ (~ (p∨ q)) ≡ ~ (~p Λ ~q)
(p Λ q) ≡ ~ (~ (p Λ q)) ≡ ~ (~p∨ ~q)
ومع ذلك فمن الأفضل استعمال العمليات المنطقية الخمس.
ك - يمكن استعمال مطابقات معروفة للحصول على مطابقات جديدة أو للبرهان على تطابق قضيتين. فمثلاً،
إنّ:
(p → q) ≡ (~q → ~p)
لأنّ:
(p → q) ≡ ~p Ú q ≡ ~q Ú ~p ≡ ~ (~q) Ú ~p ≡ (~p → ~q)
ل - إذا كانت توجد مطابقة بين قضيتين فمن الممكن الحصول على مطابقة جديدة باستبدال العمليةΛ بالعملية ∨، واستبدال العملية ∨ بالعملية Λ، واستبدال الخُلف بالمصدوقة، واستبدال المصدوقة بالخُلف.
وتدعى المطابقة الجديدة ثنوية المطابقة الأصلية، وبالتالي فكل منهما ثنوية الأخرى. ومنه، إذا كانت توجد مطابقة صحيحة بين قضيتين فإن ثنويتها تكون مطابقة صحيحة أيضاً.
مثال: إنّ القضية ~q → p Ú ~p مصدوقة، ومنه: (q → p Ú ~p) ≡ t، حيث t رمز المصدوقة. ومنه q Ú p Ú ~p ≡ t، وبالتالي فثنويتها q Λ p Λ ~p ≡ c، حيث c رمز الخُلف، وبالتالي ~q Ú ~p Ú p ≡ ~c أي: (p Λ ~p) Ú ~q ≡ t وبالتالي فالقضية p Λ ~p → ~q مصدوقة.
جبر القضايا: إنّ القوانين الآتية، لأجل أية قضايا p,q,r وحيث يرمز بـ t لأية مصدوقة و بـ c لأي خُلف، تكون محققة إذ يمكن البرهان على صحة كل منها باستخدام جدول الحقيقة (مثلاً)، ثم تستخدم هذه القوانين لبرهان صحة قضية ما:
أ ـ قانونا اللانمو:
ب ـ القانونان التجميعيان:
جـ ـ القانونان التبادليان:
د ـ القانونان التوزيعيان:
هـ ـ قوانين المحايد والماص (أو قوانين المطابقة):
و ـ قوانين الإتمام والارتداد:
ز ـ قانونا ديمورغان:
ح ـ قوانين أخرى:
(p → q) ≡ (~q → ~p)
(p → q) ≡ (~p Ú q)
~(p → q) ≡ (p Λ ~ q)
(p Λ (p ∨ q)) ≡ p
(p ∨ (p Λ q)) ≡ p
(p ↔ q) ≡ ((p → q) Λ (q → p))
(p → (p → r)) ≡ ((p Λ q) → r)
(((p → q) Λ (q → r)) → (p → r)) ≡ t
تحويل القضايا إلى قضايا لها أشكال معينة
التركيب غير الخزول: يقال عن كلٍ من المصدوقة t والخُلف c إنه قضية ثابتة، بينما يقال عن أية واحدة من القضايا الأخرى إنها غير ثابتة. ومن جهة أخرى، فإن القضية ~ X Λ y Λ X Λ ~ Z Λ y (مثلاً) تكون تركيباً ذا متغيرات X,y,Z مرتبطة ببعضها بوساطة العملية Λ فقط بعد أن زوّد بعضها بالنفي. ويمكن اختزال هذه القضية حيث تكون النتيجة هي c.
أما القضية ~X Λ ~y Λ ~Z (مثلاً) تكون تركيباً ذا متغيرات X,y,Z مرتبطة ببعضها بوساطة العملية Λ فقط بعد أن زوّدت جميعها بالنفي. ومن الواضح أنه لا يمكن اختزال هذه القضية فمن المنطقي أن تسمى تركيباً غير خزول.
وحيد الحد، أو اختصاراً الحد، مثل p هو إما خُلف c أو أية قضية غير متطابقة مع c ولكنها تركيب غير خزول بحيث يحوي عدداً محدوداً من المتغيرات التي يمكن أن يكون بعضها أو كلها مزوداً بالنفي والتي ترتبط ببعضها عدداً محدوداً من المرات بوساطة العملية فقط.
إذا كان P حداً، فإن P يكون قضية. وإذا كان هذا الحد غير متطابق مع c، فإنه لا يمكن أن يوجد متغير ونفيه بآن واحد في عبارة هذا الحد. وأيضاً، إذا كان P ≡ c وكان X أو ~X داخلاً في عبارة الحد P، فإنه لا يمكن أن يظهر X أو ~X أكثر من مرة واحدة في عبارة هذا الحد.
ليكن P أيّ حد غير متطابق مع c. يُرمز بـ L(P) لطول الحد P ويعرّف بأنه عدد العناصر الداخلة في عبارته. ويعدّ L(c)=0.
إذا كان حد مثل P يتبع لـ n متغيراً، حيث n أيّ عدد طبيعي، فإن:
0≤ L(P) ≤n
التركيب X هو حد طوله 1. والتركيب ~X هو حد طوله 1. والتركيب X Λ ~y هو حد طوله 2.
وأيضاًًL(X Λ ~y Λ Z) = L(~X Λ y Λ ~Z) = L(~X Λ ~y Λ ~Z) هو حد طوله 3.
الصيغة الناظمية الفصلية لقضية: لتكن f(X, y,….) أية قضية تتبع لعدد محدود من المتغيرات X, y,….. إذا كانت f(X, y, …) ≡ c وأمكن كتابتها على النحو:
f(x, y, …) ≡ P1ÚP2 …ÚPk (*)
حيث كل Pi هو حد غير متطابق مع خُلف c وغير متطابق أيضاً مع أيّ حد آخر Pj، حيثi, j ∋ {1, 2, …,k} و i ≠ j، فعندئذ يقال عن (∗) إنها صيغة ناظمية فصلية (أو شكل عام فصلي) للقضية المفروضة. أما إذا كانت f(x, y, …) ≡ c فإن الطرف الأيمن c من هذه المطابقة يعدّ معبرّاً عن الصيغة الناظمية الفصلية (أو الشكل العام الفصلي) لهذه القضية.
ملاحظة: ليس من الضروري أن يكون طول كل حد Pi في (∗) مساوياً عدد المتغيرات الداخلة في عبارة القضية f(X, y,…).
الصيغة الناظمية الوصلية لقضية: لتكن f(X, y,…) أية قضية تتبع لعدد محدود من المتغيرات X, y, …. إذا كانت f(X, y, …) ≡ c وأمكن كتابتها على النحو:
f(X, y, …) ≡ S1ΛS2 …ΛSk (**)
حيث كل Si هو قضية غير متطابقة مع t وغير قابلة للاختزال وتحوي عدداً محدوداً من المتغيرات التي يمكن أن يكون بعضها أو كلها مزوّداً بالنفي، والتي ترتبط ببعضها عدداً محدوداً من المرات بوساطة العملية ∨ فقط. وإضافة إلى ذلك يشترط أن تكون Si غير متطابقة مع أية قضية أخرى Sj، حيث:
i, j ∋ {1, 2, …,k) و i ≠ j
فعندئذ يقال عن (∗∗) إنها صيغة ناظمية وصلية (أو شكل عام وصلي) للقضية المفروضة.
أما إذا كانت f(x, y, …) ≡ t فإن الطرف الأيمن t من هذه المطابقة يعدّ معبّراً عن الصيّغة الناظمية الوصلية (أو الشكل العام الوصلي) لهذه القضية.
أمثلة:
أ - إن القضية (X Λ ~y) Ú (X Λ Z Λ ~X) Ú (~X Λ ~y) بشكلها الحالي لا تعدّ مكتوبة بشكل عام فصلي لأن القوس الأوسط ليس حداً. وإذا اختزلت هذه القضية فإنها تتطابق مع القضية (X Λ ~y) Ú (~X Λ ~y) التي تعبرّ عن شكل عام فصلي للقضية الأصلية. وبمتابعة الاختزال يتم الحصول على القضية غير الخزولة ~y التي تعبر عن شكل عام فصلي للقضية الأصلية ذاتها.
ب - باستخدام جبر القضايا تُختزل القضية:
f(X, y, z) ≡ (X Λ y Λ ~y) Ú(X Λ ~X) Ú (y Λ Z Λ ~Z)
بحيث تصبح f(X, y, Z) ≡ c وهذا شكل عام فصلي لها.
جـ - بأخذ القضية
f(X, y, Z) ≡ ~ (XÚ ~y) Λ ~ (X Λ ~y Λ Z)
يمكن، باستخدام قوانين جبر القضايا، ملاحظة ما يأتي:
f(X, y, Z) ≡ ~ (X Ú ~y) Ú (X Λ ~y Λ Z)
[وهذا شكل عام فصلي لـ f(X, y, Z) ]
≡ (~X Λ y) Ú (X Λ ~y Λ Z)
≡ ((~X Λ y) Ú X) Λ ((~X Λ y) Ú (~y Λ Z))
≡ (X ∨ y) Λ (~X Ú ~y) Λ (~XÚ Z) Λ (y Ú Z)
[وهذا شكل عام وصلي لـ f(X, y, Z)]
د - [القضية المفروضة]
f(X, y, Z) ≡ ~ ((X Λ ~y) ∨ (y Λ ~Z))
≡ ~ (X Λ ~y) Λ ~ (y Λ ~Z)
[شكل عام وصلي للقضية ذاتها]
≡ ~ (x Ú y) Λ (~yÚ Z)
[شكل عام فصلي للقضية نفسها]
≡ ~ (X Λ y) Ú (~X Λ Z) Ú (y Λ Z)
الشكل القانوني لقضية: إن الشكل القانوني الفصلي لقضية غير متطابقة مع خُلف c هو شكل عام فصلي لها بشرط أن يكون طول كل حد Pi مساوياً عدد المتغيرات التي تتبع لها هذه القضية.
أما إذا كانت القضية المدروسة متطابقة مع c فإن c تعبّر عن الشكل القانوني الفصلي لها.
وأيضاً، إنّ الشكل القانوني الوصلي لقضية مثل f(x, y,…), غير متطابقة مع مصدوقة t هو شكل عام وصلي لها بشرط أن يكون عدد العناصر الداخلة في عبارة كل قضية Si مساوياً عدد المتغيرات التي تتبع لها هذه القضية، مع العلم بأن العناصر الداخلة في عبارة Si هي، طبعاً، جزء من العناصر X,y, …,~X, ~y…..
أما إذا كانت f(X, y, …) ≡ t فإنّ t تعبرّ عن الشكل القانوني الوصلي لهذه القضية.
مثال: إن شكلاً عاماً فصلياً للقضية:
f(X, y, Z) ≡ ~ ((X ∨ ~y) Λ ~ (X Λ ~y Λ Z))
هو:
f(X, y, Z) ≡ (~X Λ y) ∨ (X Λ ~y Λ Z)
ولكنه ليس شكلاً قانونياً فصلياً لها لأنّ طول الحد الأول يساوي 2 بينما يجب أن يكون طوله 3 (لأن عدد المتغيرات يساوي 3). إلاّ أنه من الممكن تحويله إلى شكل قانوني فصلي لها باستخدام جبر القضايا كما يأتي:
f(X, y, Z) ≡ (~X Λ y) Λ t)∨ (X Λ ~y Λ Z) ≡ (~X Λ y) Λ (Z∨~Z)) ∨ (X Λ ~y Λ Z)
≡ (~X Λ y Λ Z) Ú (~X Λ y Λ ~Z) Ú (X Λ ~y Λ Z)
وفي الوقت ذاته، إن شكلاً عاماً وصلياً للقضية f(X, y,…) نفسها هو:
f(X, y, Z) ≡ (X Ú y) Λ (~X Ú ~y) Λ (~XÚ Z) Λ (y Ú Z)
ولكنه ليس شكلاً قانونياً وصلياً لها لأن عدد العناصر الداخلة في عبارة قضية واحدة على الأقل من القضايا الأربع، مثل القضية (~X ∨ Z)، يساوي 2 بينما يجب أن يكون هذا العدد مساوياً 3 في هذه القضية. إلاّ أنه من الممكن تحويله إلى شكل قانوني وصلي لها كما يأتي:
f(X, y, Z) ≡ ((X Ú y) Ú (Z Λ ~Z)) Λ (((~XÚ ~y) Ú (Z Λ ~Z)) Λ
((~X Ú Z) ∨ (y Λ ~y)) Λ (y ⁄Ú Z) Ú (X Λ ~X)
≡ (X Ú y Ú Z) Λ (X Ú y Ú ~Z) Λ (~X Ú ~y Ú Z) Λ (~X Ú ~y Ú ~Z) Λ (~X Ú y Ú Z)
وبمقارنة الشكلين القانونيين (الفصلي والوصلي) للقضية f(X, y, Z) ذاتها يمكن القول إن الشكل القانوني الوصلي لها ليس بثنوي الشكل القانوني الفصلي لها.
الشكل القانوني التام لقضية: إذا كان شكل قانوني فصلي، لقضية تتبع لـ n متغيراً، يحوي 2n حداً، فيقال إنه الشكل القانوني التام لهذه القضية.
مثال: الشكل القانوني التام لقضية تتبع لثلاثة متغيرات يحوي 23 حداً، أي أنه من الشكل:
(X Λ y Λ Z)Ú(~ Λ y Λ Z) Ú (X Λ ~y Λ Z) Ú (X Λ y Λ ~Z)Ú(~X Λ ~y Λ Z)Ú (~X Λ y Λ ~Z)
Ú (X Λ ~y Λ ~Z) Ú (~X Λ ~y Λ ~Z)
تعيين قضية معطاة بوساطة جدول: إذا كانت f(x) قضية بمتغير واحد x فلها أربعة أشكال مختلفة وغير متكافئة (أو غير متطابقة)، قيم الحقيقة لكل منها تظهر في الجدول الآتي:
ومن هذا الجدول يتّضح ما يأتي:
أ ـ إنّ f1(X) =1 عندما وفقط عندما X =1، وبالتالي يمكن القول إنّ f1(X) ≡ X.
ب ـ إنّ f2(X) =1 عندما وفقط عندما ~X =1، وبالتالي f2(X) ≡ ~X.
ج ـ إنّ f3(X) =1 عندما وفقط عندما X ∨ ~x =1، وبالتالي f3(X) ≡ X ∨ ~X ≡ t.
د ـ إنّ f4(X) =1 عندما وفقط عندما X Λ ~X =0، وبالتالي f4(X) ≡ X Λ ~X ≡ c.
أو بعبارة أخرى،~f4(X) =1 عندما وفقط عندما X ∨ ~X =1، وبالتالي ~f4(X) ≡ X ∨ ~X ≡ t.
ومنه فالقضية f(X) بمتغير واحد X هي إما X أو ~X أو t أو c.
وبذلك يمكن القول، في الحالة الأعم، ما يأتي:
لتعيين قضية معطاة بوساطة جدول، يتضمن قيم الحقيقة لها والمقابلة لقيم الحقيقة للمتغيرات التي تتبع لها هذه القضية، يمكن تمييز حالتين:
الحالة الأولى: إذا كانت جميع قيم الحقيقة للقضية هي 0 فإنها تتطابق مع c.
الحالة الثانية: إذا كانت توجد قيمة حقيقة، واحدة على الأقل، هي 1 لهذه القضية، فعندها يتم الاحتفاظ بتلك الأسطر من الجدول التي تقابلها القيمة1 للقضية، وتهمل الأسطر الأخرى. ومن أجل كل سطر احتُفظ به يتم تكوين حد على النحو التالي: يؤخذ كل متغير قيمته 1 ويؤخذ نفي كل متغير قيمته 0 في السطر المدروس ثم يتم تشكيل حد باستخدام العملية Λ. ثم تربط الحدود، الناتجة من الأسطر المحتفظ بها، باستخدام العملية Ú فيتم الحصول على القضية المطلوبة ممثّلة بشكل عام فصلي لها.
ملاحظة مهمة: لقد تم التركيز في الخوارزمية السابقة على قيمة الحقيقة 1 إلا أنه كان من الممكن التركيز على القيمة 0 حيث يتم تمييز الحالتين:
الحالة الأولى: إذا كانت جميع قيم الحقيقة للقضية هي 1 فإنها تتطابق مع t.
الحالة الثانية: إذا كانت توجد قيمة، واحدة على الأقل، هي 0 لهذه القضية، فعندها يتم الاحتفاظ بتلك الأسطر من الجدول التي تقابلها القيمة 1 للقضية، وتهمل الأسطر الأخرى. ومن أجل كل سطر احتُفظ به يتم تكوين قضية غير متطابقة مع t وغير قابلة للاختزال وذلك على النحو الآتي: يؤخذ كل متغير قيمته 0 ويؤخذ نفي كل متغير قيمته 1 في السطر المدروس ثم يتم تشكيل قضية باستخدام العملية Ú.
ثم تربط القضايا، الناتجة من الأسطر المحتفظ بها، باستخدام العملية Λ فيتم الحصول على القضية المطلوبة ممثّلة بشكل عام وصلي لها. ومع ذلك فإنه يفضل اختيار تلك القيمة التي تكرارها هو الأقل في الجدول من بين القيمتين 1, 0 أو بحسب متطلبات الموقف.
المنطق والدعاوى
1- مدخل أساسي: المنطق الرياضي هو، بوجه عام، تحليل لطرق التفكير. إنه المنطق الصوري الذي يهتم بالشكل أكثر من اهتمامه بالمحتوى، إذ أن ما يهمه هو أن صحة المقدمة تفرض صحة النتيجة.
وتجدر الإشارة إلى أن أية لغة لا تستطيع أن تصف بدقة عيِّنة من الأشياء إلاّ إذا كانت تحتوي على أسماء لأشياء العينة المدروسة ولصفاتها وللعلاقة بينها وبحيث تكون الأشياء المختلفة لها أسماء مختلفة. ولذلك يمكن أن يوجد في أي سرد من الألفاظ محتوى رياضي يتألف مما يلي:
أ - مفاهيم أولية يتم القبول بصحتها في البنية المدروسة.
ب - ألفاظ مميزة للأشياء الرياضية التي تقع في مجال تكوين المفاهيم.
جـ - شارات ورموز متفق عليها، وهي الرموز الأساسية في البناء الرياضي وتشتق منها الرموز الأخرى، وبإمعان النظر في تلك الشارات يمكن ملاحظة أنها إنجاز متميز لممارسات الاختزال التي تقوم بها، عادة، بنية الذكاء الفاعلة لدى الإنسان.
وبما أن القضية يُحتمل خطؤها أو تُحتمل صحتها فإن قبولها يحتاج إلى برهان ما لم تكن واضحة جداً أو من المسلّمات. فالمسلِّمة (البدهية) هي قضية أولية صحيحة لاتبرهن بل تقبل دون برهان، وتعدّ إحدى مبادئ الرياضيات. ويعطى كل تعريف بدلالة عناصر سبق تعريفها، أو مفاهيم لاتحتاج إلى تعريف، ويتم برهان كل قضية استناداً إلى قضايا كان قد جرى برهانها، أو قبلت كمسلّمة. وبالمحاكمات المنطقية يتم الحصول على نتائج جديدة ويتم بناء علم رياضي متماسك منطقياً.
والقضية الرياضية على أنواع ثلاثة، فمنها ما هو صحيح دوماً مثل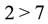
ومنها ما هو خاطئ دوماً مثل 
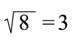، ومنها ما هو صحيح ضمن شروط معينة وخاطئ حين لا تكون هذه الشروط محققة، فمثلاً: بأخذ جميع المثلثات، فإن القول «المثلث abc قائم الزاوية» هو قضية صحيحة من أجل بعض المثلثات، وهو قضية خاطئة من أجل بقية المثلثات.
وعندما تُذكر قضية فإن ذلك يعني تحققها.
2- مبادئ الفكر: يرتكز المنطق الرياضي على افتراض مبادئ ثلاثة للفكر وهي:
أ - مبدأ الذاتية: إذا كانت A قضية رياضية معينة فإنّ:
A هي A
ب - مبدأ عدم التناقض: إذا تحققت قضية انتفى تحقق نقيضها.
جـ - مبدأ الثالث المرفوع: على كل شيء أن يتصف بصفة معينة أو بنقيضها فلا توجد حالة وسط بين القضية ونقيضها.
3- الدعاوى: الدعوى هي ادعاء بأن مجموعة من القضايا مثل S1, S2, …, Sn، وتدعى المقدمات، تنتج عنها قضية مثل S، وتدعى النتيجة.
ويرمز لمثل هذه الدعوى بالشكل الآتي:
S1, S2, …, Sn ┣ S
وتجدر الإشارة إلى أن الدعوى تكون قضية، فلها قيمة حقيقة.
فالدعوى S1, S2, …, Sn ┣ S تكون شرعية أي صحيحة إذا كانت S صحيحة كلما كانت القضايا S1, S2, …, Sn صحيحة. أو بصورة مكافئة، إذا كان،
S1 Λ S2 Λ … Λ Sn ⇒ S أي إذا كانت (S1 Λ … Λ Sn) → S مصدوقة.
فلمعرفة صحة مناقشة يمكن استخدام جدول الحقيقة وإثبات أنّ القضية (النتيجة → المقدمات) عبارة عن مصدوقة. أما إذا كانت هذه القضية ليست مصدوقة فإن المناقشة تكون غير صحيحة.
مثال: الدعوىp,p ® q q شرعية.
الحل: يكفي إثبات أنه إذا كانت p, (p ® q) صحيحتين فإن q تكون صحيحة، وذلك بكتابة جدول الحقيقة للقضية (p® q)
ومن الملاحظ أن p تكون صحيحة في حالتي السطرين الأول والثاني من أسطر هذا الجدول. أما p ® q فتكون صحيحة في حالات الأسطر الأول والثالث والرابع. ومنه فإنp,( p ® q) تكونان صحيحتين بآن واحد في حالة السطر الأول حيث q تكون صحيحة.
وبذلك تكون الدعوى صحيحة.
4- تطبيقات: يمكن استخدام القضايا في مجالات الدارات والأجهزة الآلية وجبر بول. فمثلاً، من أجل الدارات تمثّل الدارة بقضية ثم تختزل هذه القضية إلى أبسط قضية متكافئة معها ثم تؤخذ الدارة التي تمثلها القضية الأخيرة فتكون أبسط دارة متكافئة مع الدارة الأصلية (أي: للدارتين الخواص الكهربائية نفسها بالنسبة لمرور التيار الكهربائي وعدمه).
عبد الواحد أبو حمدة
_ - _
حساب القضايا
القضايا وجداول الحقيقة
قيمة الحقيقة هي إما 1 (أي صحيحة) أو 0 (أي خاطئة)، والقضية (في اللغة) هي جملة ذات معنى بحيث تكون لها قيمة حقيقة معينة تماماً، ومتغير قضية هو متغير رياضي (منطقي) يمثّل قضية، ويرمز له بالرمز p أو q أو r، والربط المنطقي هو عملية (منطقية) تستعمل لبناء قضايا جديدة انطلاقاً من قضايا معطاة، حيث تكون قيم الحقيقة للقضايا الجديدة مرتبطة بقيم الحقيقة للقضايا المعطاة.
يقال عن قضية إنها مركبة إذا كانت محوّرة عن قضية أخرى، أو كانت مؤلفة من أكثر من قضية واحدة، أي إذا كانت تحوي ربطاً منطقياً واحداً على الأقل. ويقال عن قضية إنها بسيطة إذا لم تكن مركبة.وتمثَّل القضية البسيطة، عادةً، بمتغيّر منطقي واحد.
جدول الحقيقة هو ذلك الجدول الذي يصف الدستور المعيّن لأجل عملية منطقية، أي: من أجل كل توفيق من قيم الحقيقة للقضايا البسيطة، التي تتألف منها العبارة المدروسة والمشكّلة بوساطة العملية، فإن الجدول يعطي قيمة الحقيقة للعبارة المذكورة.
يعرّف الربط الأحادي المسمى (النفي) والذي يرمز له بالرمز ~ بوساطة جدول الحقيقة الآتي:
| ~p | P |
| 0 | 1 |
| 1 | 0 |
| P Λ q | q | p |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| P Ú q | q | p |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| P → q | q | p |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| P ↔ q | q | p |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| P | q | P ¯ q | P w q | q | p |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
(1): إذا p فإن q.
(2): p شرط كاف لـ q.
(3): q شرط لازم لـ p.
(4): p تقتضي q.
وإن القضية p ↔ q تعني أية واحدة من الجمل الآتية:
(1): p إذا وفقط إذا q.
(2): كل من p,q تقتضي الأخرى.
(3): p شرط لازم وكاف لـ q.
(4): q,p متكافئتان.
وإن عدد القضايا المنطقية غير المتكافئة والتي تتبع لمتغيرين هو (16) لأنَّ كلاً من الأسطر الأربعة في جدول الحقيقة له إمكانيتان. فعلى سبيل المثال:
| P ↔ q | q | p | P | q | P ® q | P ®q | P Ú q | t | q | p |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| c | P¯ q | ~pÙ q | P Ù~ q | P Ù q | ~P | ~q | P w q | q | p |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
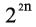عندما يكون عدد المتغيرات مساوياً n، وذلك لأنه يوجد 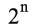سطراً في جدول الحقيقة حينئذ.ملاحظات وأمثلة:
1 - إن للأقواس في القضايا دوراً أساسياً ومهماً فهي توضح عبارة القضية وتبيّن ترتيب العمل لكتابة جدول الحقيقة لها وتزيل أيّ التباس.
ويظهر ذلك في الجدول الآتي للقضية (pÚq) → (~p Λ ~q):
| (PÚq)® (~p Λ ~q) | ~p L~ q | ~q | ~P | PÚq | q | P |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
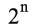سطراً فمثلاً، يمكن ملاحظة أن جدول القضية (pÚ q) → (rÚ~p) ، حيث n = 3، هو الآتي: | (PÙq)® (r~ Ú ~p) | r Ú~ p | ~p | PÙq | r | q | P |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
المصدوقات، الاقتضاء، التكافؤ
المصدوقة هي قضية صحيحة دوماً، أي أن قيمة الحقيقة لها هي 1 وذلك أياً كانت قيم الحقيقة للقضايا البسيطة التي تدخل في تكوينها.
فالقضية p → (p∨q) مصدوقة بملاحظة الجدول الآتي:
| P® (p Ú q) | p Ú q | q | P |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
فالقضية ~ (~q → (p Ú~p)) خُلف بملاحظة الجدول الآتي:
| ~(~q ® (p Ú ~p)) | ~q ®(pÚ~ p) | pÚ~p | ~q | ~p | q | P |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
والقضية (pÚq) ↔ (q Úp) مصدوقة.
وإذا رُمز للمصدوقة بالرمز t وللخُلف بالرمز c فإن:القضية ~t تكون خُلفاً، والقضية ~c تكون مصدوقة.
والقضية pÚ~p مصدوقة، والقضية p Λ ~p خُلف.
وإذا كانت القضية f (p, q,….), مصدوقة فإنّ f (f1, f2,….), تكون مصدوقة لأجل أية قضاياf1, f2,…. فمثلاً، إذا أُخذت المصدوقة (p Λ q) ↔ (q Λ p) وتمّ التعويض فيها q Λ r بـ p وp بـ q فإن القضية الناتجة: (q Λ r) Λ p↔p Λ (q Λ r) تكون مصدوقة.
يقال إنّ قضية مثل P تقتضي قضية مثل Q، ويستعمل الرمز P ⇒ Q للتعبير عن ذلك، إذا كانت Q صحيحة كلما كانت P صحيحة. ويقال، في هذه الحالة، إنّ P أقوى من Q، وإنّ Q أضعف من P.
الاقتضاء، ورمزه ⇒، يحدّد علاقة بين قضيتين، فمثلاً P ⇒ Q، يُحدّد علاقة تؤكد أن القضية P ↔ Q مصدوقة.
يقال إن قضية P تكافئ قضية Q، ويستعمل الرمز P ⇔ Q للتعبير عن ذلك، إذا كانت لهما قيم الحقيقة ذاتها أياً كانت قيم الحقيقة لمتغيراتهما. ويقال، في هذه الحالة، إن هاتين القضيتين متطابقتان ويستخدم، للتعبير عن ذلك، الرمز P ≡ Q
التكافؤ، ⇔ أو ≡، يحدد علاقة بين قضيتين، فمثلاً P ⇔ Q، يحدد علاقة تؤكد أن القضية P → Q مصدوقة.
ملاحظات ونتائج وأمثلة مهمة:
أ ـ من الممكن أن لا تكون القضية p → q مصدوقة أو خُلفاً.
ب ـ من الممكن أن لا تكون القضية p ↔ q مصدوقة أو خُلفاً.
جـ ـ أياً كانت القضايا P, Q, R فإنّ:
(1) P ⇔ p, P ⇒ p.
(2) إذا كان P ⇒ Q, Q ⇒ R فإن p ⇒ R. وأيضاً، إذا كان P ⇔ Q, Q ⇔ R فإنّ p ⇔ R.
(3) إذا كان P ⇒ Q, Q ⇒ P فإن P ≡ Q، لأنّ: [P ⇔ Q إذا وفقط إذا P ⇒ Q, Q ⇒ P].
(4) إذا كان P ⇔ Q فإنّ Q ⇔ P.
د - العلاقة ⇔ تكون علاقة تكافؤ على أية مجموعة من القضايا.
هـ - العلاقة ⇒ تكون علاقة ترتيب (جزئي) على أية مجموعة من القضايا.
و P ⇔ Q- إذا وفقط إذا P↔ Q مصدوقة.
ز - يمكن استخدام جدول الحقيقة للبرهان على تطابق قضيتين.
ح - إذا وجد متغير واحد على الأقل داخلاً في عبارة إحدى قضيتين متطابقتين ولتكن الأولى (مثلاً) وغير داخل في عبارة الثانية فهذا يعني أن قيمة الحقيقة للقضية الثانية مستقلة عن قيم الحقيقة لهذه المتغيرات غير الداخلة فيها. ادرس المثال:
(p Úq) ≡ ((rÚ~r) → (pÚq))
ط - إنّ (p → q) ≡ (~ p Ú q) بملاحظة الجدول الآتي:
| ~pÚq | P ®q | ~p | q | P |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
(p → q) ≡ (~p Ú q)
(p ↔ q) ≡ ((p → q) Λ (q → p))
وإضافة إلى ذلك، يمكن الاكتفاء بالعمليتين Λ, ~ أو بالعمليتين Ú, ~ بملاحظة المطابقات:
~ (p Ú q) ≡ ~ p Λ ~q
~ (p Λ q) ≡ ~ pÚ ~q
~ (~p) ≡ p
وبالتالي:
(p ∨ q) ≡ ~ (~ (p∨ q)) ≡ ~ (~p Λ ~q)
(p Λ q) ≡ ~ (~ (p Λ q)) ≡ ~ (~p∨ ~q)
ومع ذلك فمن الأفضل استعمال العمليات المنطقية الخمس.
ك - يمكن استعمال مطابقات معروفة للحصول على مطابقات جديدة أو للبرهان على تطابق قضيتين. فمثلاً،
إنّ:
(p → q) ≡ (~q → ~p)
لأنّ:
(p → q) ≡ ~p Ú q ≡ ~q Ú ~p ≡ ~ (~q) Ú ~p ≡ (~p → ~q)
ل - إذا كانت توجد مطابقة بين قضيتين فمن الممكن الحصول على مطابقة جديدة باستبدال العمليةΛ بالعملية ∨، واستبدال العملية ∨ بالعملية Λ، واستبدال الخُلف بالمصدوقة، واستبدال المصدوقة بالخُلف.
وتدعى المطابقة الجديدة ثنوية المطابقة الأصلية، وبالتالي فكل منهما ثنوية الأخرى. ومنه، إذا كانت توجد مطابقة صحيحة بين قضيتين فإن ثنويتها تكون مطابقة صحيحة أيضاً.
مثال: إنّ القضية ~q → p Ú ~p مصدوقة، ومنه: (q → p Ú ~p) ≡ t، حيث t رمز المصدوقة. ومنه q Ú p Ú ~p ≡ t، وبالتالي فثنويتها q Λ p Λ ~p ≡ c، حيث c رمز الخُلف، وبالتالي ~q Ú ~p Ú p ≡ ~c أي: (p Λ ~p) Ú ~q ≡ t وبالتالي فالقضية p Λ ~p → ~q مصدوقة.
جبر القضايا: إنّ القوانين الآتية، لأجل أية قضايا p,q,r وحيث يرمز بـ t لأية مصدوقة و بـ c لأي خُلف، تكون محققة إذ يمكن البرهان على صحة كل منها باستخدام جدول الحقيقة (مثلاً)، ثم تستخدم هذه القوانين لبرهان صحة قضية ما:
أ ـ قانونا اللانمو:
| (1) | p Ú p ≡ p | (1َ) | p Λ p ≡ p |
| (1) | (pÚ q) Ú r ≡ p Ú (q Ú r) | (1َ) | (p Λ q) Λ r ≡ p Λ (q Λ r) |
| (1) | pÚ q ≡ q Ú p | (1َ) | p Λ q ≡ q Λ p |
| (1) | p Ú (q Λ r) ≡ (p Ú q) Λ (pÚ r) | (1َ) | p Λ (q Ú r) ≡ (p Λ q) Ú (p Λ r) |
| (1) | p ∨ c ≡ p | (1َ) | p Λ t ≡ p |
| (2) | p ∨ ct ≡ t | (2َ) | p Λ c ≡ c |
| (1) | p Ú ~p ≡ t | (1َ) | p Λ ~ p≡ c |
| (2) | ~t ≡ c | (2َ) | ~c ≡ t |
| (3) | ~ (~p) ≡ p |
| (1) | ~(p Ú q) ≡ ~p Λ ~q | (1َ) | ~(p Λ q) ≡ ~p Ú ~q |
(p → q) ≡ (~q → ~p)
(p → q) ≡ (~p Ú q)
~(p → q) ≡ (p Λ ~ q)
(p Λ (p ∨ q)) ≡ p
(p ∨ (p Λ q)) ≡ p
(p ↔ q) ≡ ((p → q) Λ (q → p))
(p → (p → r)) ≡ ((p Λ q) → r)
(((p → q) Λ (q → r)) → (p → r)) ≡ t
تحويل القضايا إلى قضايا لها أشكال معينة
التركيب غير الخزول: يقال عن كلٍ من المصدوقة t والخُلف c إنه قضية ثابتة، بينما يقال عن أية واحدة من القضايا الأخرى إنها غير ثابتة. ومن جهة أخرى، فإن القضية ~ X Λ y Λ X Λ ~ Z Λ y (مثلاً) تكون تركيباً ذا متغيرات X,y,Z مرتبطة ببعضها بوساطة العملية Λ فقط بعد أن زوّد بعضها بالنفي. ويمكن اختزال هذه القضية حيث تكون النتيجة هي c.
أما القضية ~X Λ ~y Λ ~Z (مثلاً) تكون تركيباً ذا متغيرات X,y,Z مرتبطة ببعضها بوساطة العملية Λ فقط بعد أن زوّدت جميعها بالنفي. ومن الواضح أنه لا يمكن اختزال هذه القضية فمن المنطقي أن تسمى تركيباً غير خزول.
وحيد الحد، أو اختصاراً الحد، مثل p هو إما خُلف c أو أية قضية غير متطابقة مع c ولكنها تركيب غير خزول بحيث يحوي عدداً محدوداً من المتغيرات التي يمكن أن يكون بعضها أو كلها مزوداً بالنفي والتي ترتبط ببعضها عدداً محدوداً من المرات بوساطة العملية فقط.
إذا كان P حداً، فإن P يكون قضية. وإذا كان هذا الحد غير متطابق مع c، فإنه لا يمكن أن يوجد متغير ونفيه بآن واحد في عبارة هذا الحد. وأيضاً، إذا كان P ≡ c وكان X أو ~X داخلاً في عبارة الحد P، فإنه لا يمكن أن يظهر X أو ~X أكثر من مرة واحدة في عبارة هذا الحد.
ليكن P أيّ حد غير متطابق مع c. يُرمز بـ L(P) لطول الحد P ويعرّف بأنه عدد العناصر الداخلة في عبارته. ويعدّ L(c)=0.
إذا كان حد مثل P يتبع لـ n متغيراً، حيث n أيّ عدد طبيعي، فإن:
0≤ L(P) ≤n
التركيب X هو حد طوله 1. والتركيب ~X هو حد طوله 1. والتركيب X Λ ~y هو حد طوله 2.
وأيضاًًL(X Λ ~y Λ Z) = L(~X Λ y Λ ~Z) = L(~X Λ ~y Λ ~Z) هو حد طوله 3.
الصيغة الناظمية الفصلية لقضية: لتكن f(X, y,….) أية قضية تتبع لعدد محدود من المتغيرات X, y,….. إذا كانت f(X, y, …) ≡ c وأمكن كتابتها على النحو:
f(x, y, …) ≡ P1ÚP2 …ÚPk (*)
حيث كل Pi هو حد غير متطابق مع خُلف c وغير متطابق أيضاً مع أيّ حد آخر Pj، حيثi, j ∋ {1, 2, …,k} و i ≠ j، فعندئذ يقال عن (∗) إنها صيغة ناظمية فصلية (أو شكل عام فصلي) للقضية المفروضة. أما إذا كانت f(x, y, …) ≡ c فإن الطرف الأيمن c من هذه المطابقة يعدّ معبرّاً عن الصيغة الناظمية الفصلية (أو الشكل العام الفصلي) لهذه القضية.
ملاحظة: ليس من الضروري أن يكون طول كل حد Pi في (∗) مساوياً عدد المتغيرات الداخلة في عبارة القضية f(X, y,…).
الصيغة الناظمية الوصلية لقضية: لتكن f(X, y,…) أية قضية تتبع لعدد محدود من المتغيرات X, y, …. إذا كانت f(X, y, …) ≡ c وأمكن كتابتها على النحو:
f(X, y, …) ≡ S1ΛS2 …ΛSk (**)
حيث كل Si هو قضية غير متطابقة مع t وغير قابلة للاختزال وتحوي عدداً محدوداً من المتغيرات التي يمكن أن يكون بعضها أو كلها مزوّداً بالنفي، والتي ترتبط ببعضها عدداً محدوداً من المرات بوساطة العملية ∨ فقط. وإضافة إلى ذلك يشترط أن تكون Si غير متطابقة مع أية قضية أخرى Sj، حيث:
i, j ∋ {1, 2, …,k) و i ≠ j
فعندئذ يقال عن (∗∗) إنها صيغة ناظمية وصلية (أو شكل عام وصلي) للقضية المفروضة.
أما إذا كانت f(x, y, …) ≡ t فإن الطرف الأيمن t من هذه المطابقة يعدّ معبّراً عن الصيّغة الناظمية الوصلية (أو الشكل العام الوصلي) لهذه القضية.
أمثلة:
أ - إن القضية (X Λ ~y) Ú (X Λ Z Λ ~X) Ú (~X Λ ~y) بشكلها الحالي لا تعدّ مكتوبة بشكل عام فصلي لأن القوس الأوسط ليس حداً. وإذا اختزلت هذه القضية فإنها تتطابق مع القضية (X Λ ~y) Ú (~X Λ ~y) التي تعبرّ عن شكل عام فصلي للقضية الأصلية. وبمتابعة الاختزال يتم الحصول على القضية غير الخزولة ~y التي تعبر عن شكل عام فصلي للقضية الأصلية ذاتها.
ب - باستخدام جبر القضايا تُختزل القضية:
f(X, y, z) ≡ (X Λ y Λ ~y) Ú(X Λ ~X) Ú (y Λ Z Λ ~Z)
بحيث تصبح f(X, y, Z) ≡ c وهذا شكل عام فصلي لها.
جـ - بأخذ القضية
f(X, y, Z) ≡ ~ (XÚ ~y) Λ ~ (X Λ ~y Λ Z)
يمكن، باستخدام قوانين جبر القضايا، ملاحظة ما يأتي:
f(X, y, Z) ≡ ~ (X Ú ~y) Ú (X Λ ~y Λ Z)
[وهذا شكل عام فصلي لـ f(X, y, Z) ]
≡ (~X Λ y) Ú (X Λ ~y Λ Z)
≡ ((~X Λ y) Ú X) Λ ((~X Λ y) Ú (~y Λ Z))
≡ (X ∨ y) Λ (~X Ú ~y) Λ (~XÚ Z) Λ (y Ú Z)
[وهذا شكل عام وصلي لـ f(X, y, Z)]
د - [القضية المفروضة]
f(X, y, Z) ≡ ~ ((X Λ ~y) ∨ (y Λ ~Z))
≡ ~ (X Λ ~y) Λ ~ (y Λ ~Z)
[شكل عام وصلي للقضية ذاتها]
≡ ~ (x Ú y) Λ (~yÚ Z)
[شكل عام فصلي للقضية نفسها]
≡ ~ (X Λ y) Ú (~X Λ Z) Ú (y Λ Z)
الشكل القانوني لقضية: إن الشكل القانوني الفصلي لقضية غير متطابقة مع خُلف c هو شكل عام فصلي لها بشرط أن يكون طول كل حد Pi مساوياً عدد المتغيرات التي تتبع لها هذه القضية.
أما إذا كانت القضية المدروسة متطابقة مع c فإن c تعبّر عن الشكل القانوني الفصلي لها.
وأيضاً، إنّ الشكل القانوني الوصلي لقضية مثل f(x, y,…), غير متطابقة مع مصدوقة t هو شكل عام وصلي لها بشرط أن يكون عدد العناصر الداخلة في عبارة كل قضية Si مساوياً عدد المتغيرات التي تتبع لها هذه القضية، مع العلم بأن العناصر الداخلة في عبارة Si هي، طبعاً، جزء من العناصر X,y, …,~X, ~y…..
أما إذا كانت f(X, y, …) ≡ t فإنّ t تعبرّ عن الشكل القانوني الوصلي لهذه القضية.
مثال: إن شكلاً عاماً فصلياً للقضية:
f(X, y, Z) ≡ ~ ((X ∨ ~y) Λ ~ (X Λ ~y Λ Z))
هو:
f(X, y, Z) ≡ (~X Λ y) ∨ (X Λ ~y Λ Z)
ولكنه ليس شكلاً قانونياً فصلياً لها لأنّ طول الحد الأول يساوي 2 بينما يجب أن يكون طوله 3 (لأن عدد المتغيرات يساوي 3). إلاّ أنه من الممكن تحويله إلى شكل قانوني فصلي لها باستخدام جبر القضايا كما يأتي:
f(X, y, Z) ≡ (~X Λ y) Λ t)∨ (X Λ ~y Λ Z) ≡ (~X Λ y) Λ (Z∨~Z)) ∨ (X Λ ~y Λ Z)
≡ (~X Λ y Λ Z) Ú (~X Λ y Λ ~Z) Ú (X Λ ~y Λ Z)
وفي الوقت ذاته، إن شكلاً عاماً وصلياً للقضية f(X, y,…) نفسها هو:
f(X, y, Z) ≡ (X Ú y) Λ (~X Ú ~y) Λ (~XÚ Z) Λ (y Ú Z)
ولكنه ليس شكلاً قانونياً وصلياً لها لأن عدد العناصر الداخلة في عبارة قضية واحدة على الأقل من القضايا الأربع، مثل القضية (~X ∨ Z)، يساوي 2 بينما يجب أن يكون هذا العدد مساوياً 3 في هذه القضية. إلاّ أنه من الممكن تحويله إلى شكل قانوني وصلي لها كما يأتي:
f(X, y, Z) ≡ ((X Ú y) Ú (Z Λ ~Z)) Λ (((~XÚ ~y) Ú (Z Λ ~Z)) Λ
((~X Ú Z) ∨ (y Λ ~y)) Λ (y ⁄Ú Z) Ú (X Λ ~X)
≡ (X Ú y Ú Z) Λ (X Ú y Ú ~Z) Λ (~X Ú ~y Ú Z) Λ (~X Ú ~y Ú ~Z) Λ (~X Ú y Ú Z)
وبمقارنة الشكلين القانونيين (الفصلي والوصلي) للقضية f(X, y, Z) ذاتها يمكن القول إن الشكل القانوني الوصلي لها ليس بثنوي الشكل القانوني الفصلي لها.
الشكل القانوني التام لقضية: إذا كان شكل قانوني فصلي، لقضية تتبع لـ n متغيراً، يحوي 2n حداً، فيقال إنه الشكل القانوني التام لهذه القضية.
مثال: الشكل القانوني التام لقضية تتبع لثلاثة متغيرات يحوي 23 حداً، أي أنه من الشكل:
(X Λ y Λ Z)Ú(~ Λ y Λ Z) Ú (X Λ ~y Λ Z) Ú (X Λ y Λ ~Z)Ú(~X Λ ~y Λ Z)Ú (~X Λ y Λ ~Z)
Ú (X Λ ~y Λ ~Z) Ú (~X Λ ~y Λ ~Z)
تعيين قضية معطاة بوساطة جدول: إذا كانت f(x) قضية بمتغير واحد x فلها أربعة أشكال مختلفة وغير متكافئة (أو غير متطابقة)، قيم الحقيقة لكل منها تظهر في الجدول الآتي:
| f4(X) | f3(X) | f2(X) | f1(X) | X |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
أ ـ إنّ f1(X) =1 عندما وفقط عندما X =1، وبالتالي يمكن القول إنّ f1(X) ≡ X.
ب ـ إنّ f2(X) =1 عندما وفقط عندما ~X =1، وبالتالي f2(X) ≡ ~X.
ج ـ إنّ f3(X) =1 عندما وفقط عندما X ∨ ~x =1، وبالتالي f3(X) ≡ X ∨ ~X ≡ t.
د ـ إنّ f4(X) =1 عندما وفقط عندما X Λ ~X =0، وبالتالي f4(X) ≡ X Λ ~X ≡ c.
أو بعبارة أخرى،~f4(X) =1 عندما وفقط عندما X ∨ ~X =1، وبالتالي ~f4(X) ≡ X ∨ ~X ≡ t.
ومنه فالقضية f(X) بمتغير واحد X هي إما X أو ~X أو t أو c.
وبذلك يمكن القول، في الحالة الأعم، ما يأتي:
لتعيين قضية معطاة بوساطة جدول، يتضمن قيم الحقيقة لها والمقابلة لقيم الحقيقة للمتغيرات التي تتبع لها هذه القضية، يمكن تمييز حالتين:
الحالة الأولى: إذا كانت جميع قيم الحقيقة للقضية هي 0 فإنها تتطابق مع c.
الحالة الثانية: إذا كانت توجد قيمة حقيقة، واحدة على الأقل، هي 1 لهذه القضية، فعندها يتم الاحتفاظ بتلك الأسطر من الجدول التي تقابلها القيمة1 للقضية، وتهمل الأسطر الأخرى. ومن أجل كل سطر احتُفظ به يتم تكوين حد على النحو التالي: يؤخذ كل متغير قيمته 1 ويؤخذ نفي كل متغير قيمته 0 في السطر المدروس ثم يتم تشكيل حد باستخدام العملية Λ. ثم تربط الحدود، الناتجة من الأسطر المحتفظ بها، باستخدام العملية Ú فيتم الحصول على القضية المطلوبة ممثّلة بشكل عام فصلي لها.
ملاحظة مهمة: لقد تم التركيز في الخوارزمية السابقة على قيمة الحقيقة 1 إلا أنه كان من الممكن التركيز على القيمة 0 حيث يتم تمييز الحالتين:
الحالة الأولى: إذا كانت جميع قيم الحقيقة للقضية هي 1 فإنها تتطابق مع t.
الحالة الثانية: إذا كانت توجد قيمة، واحدة على الأقل، هي 0 لهذه القضية، فعندها يتم الاحتفاظ بتلك الأسطر من الجدول التي تقابلها القيمة 1 للقضية، وتهمل الأسطر الأخرى. ومن أجل كل سطر احتُفظ به يتم تكوين قضية غير متطابقة مع t وغير قابلة للاختزال وذلك على النحو الآتي: يؤخذ كل متغير قيمته 0 ويؤخذ نفي كل متغير قيمته 1 في السطر المدروس ثم يتم تشكيل قضية باستخدام العملية Ú.
ثم تربط القضايا، الناتجة من الأسطر المحتفظ بها، باستخدام العملية Λ فيتم الحصول على القضية المطلوبة ممثّلة بشكل عام وصلي لها. ومع ذلك فإنه يفضل اختيار تلك القيمة التي تكرارها هو الأقل في الجدول من بين القيمتين 1, 0 أو بحسب متطلبات الموقف.
المنطق والدعاوى
1- مدخل أساسي: المنطق الرياضي هو، بوجه عام، تحليل لطرق التفكير. إنه المنطق الصوري الذي يهتم بالشكل أكثر من اهتمامه بالمحتوى، إذ أن ما يهمه هو أن صحة المقدمة تفرض صحة النتيجة.
وتجدر الإشارة إلى أن أية لغة لا تستطيع أن تصف بدقة عيِّنة من الأشياء إلاّ إذا كانت تحتوي على أسماء لأشياء العينة المدروسة ولصفاتها وللعلاقة بينها وبحيث تكون الأشياء المختلفة لها أسماء مختلفة. ولذلك يمكن أن يوجد في أي سرد من الألفاظ محتوى رياضي يتألف مما يلي:
أ - مفاهيم أولية يتم القبول بصحتها في البنية المدروسة.
ب - ألفاظ مميزة للأشياء الرياضية التي تقع في مجال تكوين المفاهيم.
جـ - شارات ورموز متفق عليها، وهي الرموز الأساسية في البناء الرياضي وتشتق منها الرموز الأخرى، وبإمعان النظر في تلك الشارات يمكن ملاحظة أنها إنجاز متميز لممارسات الاختزال التي تقوم بها، عادة، بنية الذكاء الفاعلة لدى الإنسان.
وبما أن القضية يُحتمل خطؤها أو تُحتمل صحتها فإن قبولها يحتاج إلى برهان ما لم تكن واضحة جداً أو من المسلّمات. فالمسلِّمة (البدهية) هي قضية أولية صحيحة لاتبرهن بل تقبل دون برهان، وتعدّ إحدى مبادئ الرياضيات. ويعطى كل تعريف بدلالة عناصر سبق تعريفها، أو مفاهيم لاتحتاج إلى تعريف، ويتم برهان كل قضية استناداً إلى قضايا كان قد جرى برهانها، أو قبلت كمسلّمة. وبالمحاكمات المنطقية يتم الحصول على نتائج جديدة ويتم بناء علم رياضي متماسك منطقياً.
والقضية الرياضية على أنواع ثلاثة، فمنها ما هو صحيح دوماً مثل
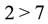ومنها ما هو خاطئ دوماً مثل 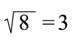، ومنها ما هو صحيح ضمن شروط معينة وخاطئ حين لا تكون هذه الشروط محققة، فمثلاً: بأخذ جميع المثلثات، فإن القول «المثلث abc قائم الزاوية» هو قضية صحيحة من أجل بعض المثلثات، وهو قضية خاطئة من أجل بقية المثلثات.وعندما تُذكر قضية فإن ذلك يعني تحققها.
2- مبادئ الفكر: يرتكز المنطق الرياضي على افتراض مبادئ ثلاثة للفكر وهي:
أ - مبدأ الذاتية: إذا كانت A قضية رياضية معينة فإنّ:
A هي A
ب - مبدأ عدم التناقض: إذا تحققت قضية انتفى تحقق نقيضها.
جـ - مبدأ الثالث المرفوع: على كل شيء أن يتصف بصفة معينة أو بنقيضها فلا توجد حالة وسط بين القضية ونقيضها.
3- الدعاوى: الدعوى هي ادعاء بأن مجموعة من القضايا مثل S1, S2, …, Sn، وتدعى المقدمات، تنتج عنها قضية مثل S، وتدعى النتيجة.
ويرمز لمثل هذه الدعوى بالشكل الآتي:
S1, S2, …, Sn ┣ S
وتجدر الإشارة إلى أن الدعوى تكون قضية، فلها قيمة حقيقة.
فالدعوى S1, S2, …, Sn ┣ S تكون شرعية أي صحيحة إذا كانت S صحيحة كلما كانت القضايا S1, S2, …, Sn صحيحة. أو بصورة مكافئة، إذا كان،
S1 Λ S2 Λ … Λ Sn ⇒ S أي إذا كانت (S1 Λ … Λ Sn) → S مصدوقة.
فلمعرفة صحة مناقشة يمكن استخدام جدول الحقيقة وإثبات أنّ القضية (النتيجة → المقدمات) عبارة عن مصدوقة. أما إذا كانت هذه القضية ليست مصدوقة فإن المناقشة تكون غير صحيحة.
مثال: الدعوىp,p ® q q شرعية.
الحل: يكفي إثبات أنه إذا كانت p, (p ® q) صحيحتين فإن q تكون صحيحة، وذلك بكتابة جدول الحقيقة للقضية (p® q)
| P ® q | q | p |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
وبذلك تكون الدعوى صحيحة.
4- تطبيقات: يمكن استخدام القضايا في مجالات الدارات والأجهزة الآلية وجبر بول. فمثلاً، من أجل الدارات تمثّل الدارة بقضية ثم تختزل هذه القضية إلى أبسط قضية متكافئة معها ثم تؤخذ الدارة التي تمثلها القضية الأخيرة فتكون أبسط دارة متكافئة مع الدارة الأصلية (أي: للدارتين الخواص الكهربائية نفسها بالنسبة لمرور التيار الكهربائي وعدمه).
عبد الواحد أبو حمدة