تويت
حساب عددي
numerical calculation - Calcul numérique
الحساب العددي
تعريف الحساب العددي وأهميته
الحساب العددي هو مجموعة طرائق تؤدي إلى حلول عددية لعددٍ من المسائل. فالتطور العملي والتقني الهائل وجّه الأنظار إلى أن عدداً كبيراً من المسائل العلمية، الرياضية والفيزيائية والهندسية، يتعذر إيجاد حلول عملية لها بالطرائق التحليلية، مما دفع العلماء إلى البحث عن طرائق عددية لحل تلك المسائل وتطوير تلك الطرائق وبرمجتها بحيث يستفاد من القدرة الهائلة للحواسيب، الأمر الذي جعل علم الحساب العددي في مقدمة العلوم التطبيقية الحديثة.
ولعل أهم المسائل التي يعالجها هذا العلم
حل المعادلات الجبرية - إيجاد مجموع متسلسلة عددية[ر] - إيجاد قيم تكامل محدَّد[ر] - حساب مشتق دالة عند نقط معيّنة - إيجاد حل معادلة تفاضلية عادية أو جزئية عند نقط معيّنة - حل مجموعة معادلات خطية... إضافة إلى إعطاء الخوارزميات[ر] ووضع البرامج اللازمة لحل تلك المسائل وتقدير الأخطاء المرتكبة.
المصادر الرئيسة للأخطاء
تتضمن كل مسألة من مسائل الحساب العددي معطيات أولية وخوارزميات ونتائج عددية، ويندر أن تكون قيم المعطيات الأولية معلومة بدقة تامة لأنها إما أن تنتج عن قياسات تقرييية لا تخلو من الخطأ، أو عن قوانين وصيغ تقريبية، أو أنها تحتوي على ثوابت يتعذر تحديد قيمها الدقيقة كالعدد π أو e مثلاً.
وكذلك فإن الخوارزميات وطرائق إيجاد الحلول العددية تضيف أخطاءً جديدة سرعان ما تتراكم بسبب تكرار العمليات الحسابية، كما أن النتائج العددية غالباً ما تكون كسرية غير منتهية ولا يمكن التعبير عنها بعدد منته من الأرقام، الأمر الذي يدعو إلى تدوير الأعداد والاكتفاء بعدد من الأرقام يناسب طول جملة الحاسوب، وقد اصطلح على إجراء التدوير بالشكل التالي:
ننظر إلى أول الأرقام المحذوفة (الرقم الأيسر منها)، فإن كان أكبر من 5، أضفنا إلى آخر رقم غير محذوف واحداً، أما إذا كان أول الأرقام المحذوفة أصغر من 5 حافظنا على الأرقام غير المحذوفة دون تغيير، فالعدد 3.75243 يمكن أن يُدوَّر إلى 3.75 والعدد 3.7572 يمكن أن يدوَّر إلى 3.76. أما إذا كان أول الأرقام المحذوفة 5، فإن كان على يمينه أرقام أخرى أضفنا إلى آخر رقم غير محذوف واحداً. وإذا لم يكن على يمينه أرقام أخرى فإننا ندوِّر العدد بحيث يصبح آخر رقم غير محذوف زوجياً فالعدد 3.6752 يمكن أن يدور إلى 3.68 والعدد 3.635 إلى 3.64 والعدد 3.625 إلى 3.62.
الخطأ المطلق
يستدل مما سبق على أنه من الضروري في كثير من الأحيان اعتماد قيمة تقريبية ب عوضاً عن القيمة الدقيقة لعدد ما س0 يسمى الفرق |ب-س| بين القيمة الدقيقة والقيمة التقريبية بالخطأ المطلق، وتحسب عادة قيمة عظمى لهذا الخطأ يرمز لها بـ Î وهي تحدِّد مقدار الدقة في حساب العدد س، فلو وجد مثلاً أن القيمة التقريبية لجذرٍ للمعادلة س3 – س - 1 = 0 هي س = 1.3247 وأن القيمة العظمى للخطأ المرتكب تساوي 5 × 10-5 فإن هذا يعني أن القيمة الدقيقة للجذر س1 محصورة في الفترة (مجال): 1.32465 < س1 < 1.32475
وإذا قيل إن العدد ب = 1.57 مدوَّر، فإن هذا يعني أن القيمة الدقيقة تقع في الفترة 1.565 ³ ب ³ 1.575.
الحساب التقريبي لجذر معادلة
1- طريقة تنصيف الفترة:
إذا كانت الدالة تا(س) مستمرة على الفترة (المجال) [ب،جـ] وتحقق الشرط:
تا(ب) . تا(جـ) < 0 كان للمعادلة تا(س) =0 جذر في الفترة [ب،جـ]. تعتبر القيمة:
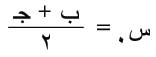
قيمة تقريبية لهذا الجذر، وبحسب المقدار تا (س0)، فإذا تحقق الشرط تا(س0) . تا(ب) <0، كان للمعادلة جذر في الفترة [ب،س0]. تعتبر القيمة:
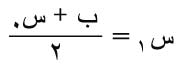
قيمة تقريبية جديدة للجذر، وهكذا تنصف الفترة [بن، جـن] الحاوية على الجذر في كل مرة، ويكتب دستور حساب القيمة التقريبية للجذر على النحو التالي:
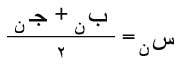
وتكون القيمة العظمى للخطأ المرتكب:
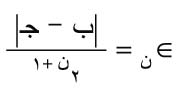
2- طريقة نيوتن:
إذا كانت الدالة تا(س) مُعرّفة على الفترة [ب، جـ] وإذا كان المشتقان الأول والثاني لها مُعرفين على الفترة السابقة وتاَ(س) ≠ 0 و تاً(س)≠ 0 " س ' [ب، جـ] فإن القيمة التقريبية لجذر المعادلة تا(س) =0 تحسب من الدستور:
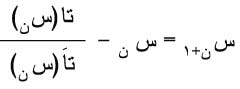
بدءاً من قيمة ابتدائية س0 وتتعين القيمة العظمى للخطأ المرتكب من العلاقة:
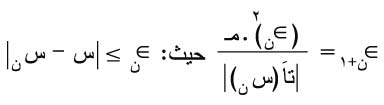
وَ مـ هي قيمة عظمى لـ |تاً(س)| في الفترة [ب، حـ].
مثال: للبحث عن جذر للمعادلة س3 – س – 1 = 0 يلاحظ أن تا(1). تا(2) = - 5 مما يدل على أن لها جذراً في الفترة [2،1] تطبق طريقة تنصيف الفترة لتعيين هذا الجذر فتنتج القيم:
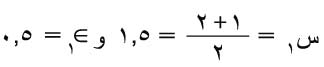
وتا(1) . تا(1.5)<0
............................................................................................. .....................
...........................................
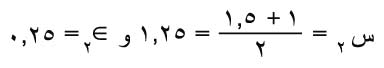
س20 = 1.3247175 ويكون تا(س20) = -1.8×10-6
أما إذا طبقت طريقة نيوتن لتعيين هذا الجذر فإن النتائج تكون بفرض س0 = 1 على النحو: س1 = 1.5، س2 = 1.3478261، س4 = 1.3247181
ويكون تا(س4) 9×10-7، مما يدل على أن النتيجة تقترب من الحل الدقيق حسب هذه الطريقة بسرعة كبيرة.
الحساب التقريبي لمجموع متسلسلة عددية[ر]:
إن المجموع مج لمتسلسلة عددية متقاربة ذات حدود موجبة يكتب على النحو: مج = مجن + قن حيث مجن هو المجموع الجزئي للحدود ن الأولى من المتسلسلة وقن الباقي الذي يسعى إلى الصفر عندما ن ¬ ¥ إذا كانت المتسلسلة متقاربة.
لا يمكن حساب المجموع مج بدقة تامة في كثير من الحالات، لذا تعتبر القيمة مجن قيمة تقريبية لهذا المجموع، ويكون الخطأ المرتكب عندها يساوي قن، ولما كان حساب قن بدوره غير ممكن لذا تحسب قيمة عظمى لهذا الباقي ويتم ذلك كما يلي:
1- معيار كوشي Cauchy: إذا وجد عدد صحيح ط، بحيث أنه أياّ كان:
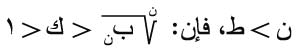
فإن المتسلسلة ذات الحد العام بن تكون متقاربة، وتحسب القيمة العظمى للباقي ن من العلاقة:
2- معيار دالمبير D’alambert: إذا وجد عدد طبيعي ط بحيث أنه أياً كان:
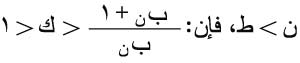
فعندئذٍ تحسب القيمة العظمى للباقي من العلاقة:
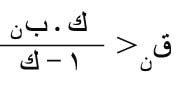
3- إذا كانت المتسلسلة ذات الحد العام بن متناوبة فإن القيمة العظمى للباقي قن تحسب من العبارة:
|قن|<|بن+1|
أما من الناحية العملية فلحساب مجموع متسلسلة بخطأ لايتجاوز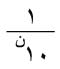
، يُحسب مجموع عدد من الحدود الأولى تسبق الحد الذي تنعدم فيه ن + 2 من الأرقام العشرية الأولى وليكن عدد هذه الحدود ط، ويراعى خلال الحساب أن تكون الدقة في حساب قيمة كل من الحدود تفوق 
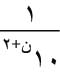فيصبح الخطأ الكلي المرتكب:
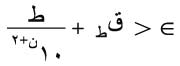
وتكون النتيجة على الغالب في حدود الدقة المطلوبة، فإن لم يتحقق ذلك أضيف إلى المجموع الجزئي مجط عدد مناسب من الحدود.
مثال: تحسب قيمة تقريبية لـ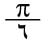
بخطأ لايتجاوز 
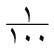من المتسلسلة:
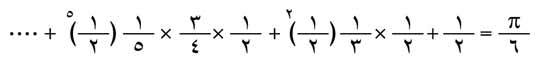
يكتفى بثلاثة حدود فينتج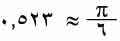
. وتكون القيمة العظمى للخطأ 
.
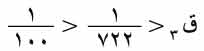الحساب التقريبي لتكامل محدَّد[ر]:
1- طريقة النشر بمتسلسلة: لحساب قيمة التكامل المحدَّد :
تُنْشر الدالة تا(س) في متسلسلة صحيحة تحوي فترة تقاربها الفترة [ب، جـ] فيكون:
تا(س) = د0+ د1س+ د2س2+...+ دنسن+...
تُكامل المتسلسلة الناتجة حداً حداً فينتج:
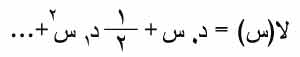
وتكون قيمة التكامل المطلوبة هي:
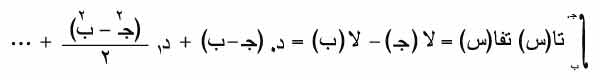
ويتم المطلوب بحساب مجموع المتسلسلة الناتجة بشكل تقريبي.
2- طريقة أشباه المنحرف: تقسم الفترة [ب، جـ] إلى فترات جزئية متساوية عددها ن ويقام من نقط التقسيم س0=ب،س1،....سن=جـ مستقيمات تعامد محور السينات إن طول كل فترة جزئية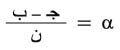
يحسب مجموع سطوح أشباه المنحرف الناتجة عن استبدال أوتار أقواس المنحني بيان الدالة تا(س) في الفترات الجزئية بهذه الأقواس ويعتبر هذا المجموع قيمة تقريبية للتكامل المحدد ويكتب:
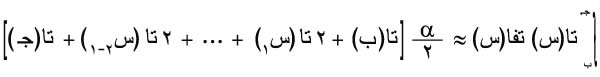
وتحسب القيمة العظمى للخطأ المرتكب من العلاقة:
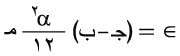
حيث مـ هي قيمة عظمى لـ | تاً(س)| في الفترة [ب، جـ].
وتزداد دقة الحساب بزيادة عدد الفترات الجزئية.
مثال: لحساب التكامل المحدد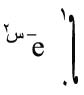
يطبق دستور أشباه المنحرف بفرض:
فتنتج القيمة:
تحسب القيمة العظمى للخطأ فتكون:
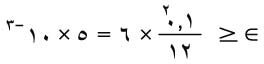
حساب مشتق دالة عند نقطة معينة بشكل تقريبي:
طريقة تايلور Taylor: لتعيين مشتق الدالة تا(س) عند نقطة س0 معينة تنشر الدالة في متسلسلة صحيحة بجوار س0 ويكتفى بثلاثة حدود فقط فيكون:
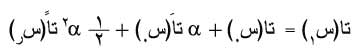
حيث:
س1- س0 = a، س0< سر< س1
ويحسب تاَ(س0) فيكون:
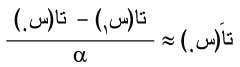
وتكون القيمة العظمى للخطأ:
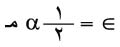
بفرض مـ هي القيمة العظمى لـ |تاً(س)| .
إيجاد حل معادلة تفاضلية عند نقطة معينة بشكل تقريبي:
طريقة أولر Euler: لإيجاد حل المعادلة التفاضلية:
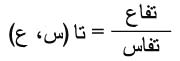
التي تحقق الشرط ع = ع0 عندما س = س0 عند النقطة (سن+1، عن+1) تنشر الدالة ع (س) بجوار سن وتكتب العلاقة:
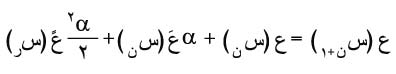
حيث:
a = سن+1 – سن، سن ³ سر ³ سن+1
ويكتب دستور أولر على النحو:
ع(سن+1) = ع(سن) + a تا(سن،عن)
وتكون القيمة العظمى للخطأ المرتكب:
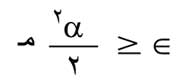
وذلك بفرض أن مـ قيمة عظمى لـ | عً (س)|
يطبق الدستور السابق بصورة مكررة توخياً للدقة.
مثال: لإيجاد حل المعادلة التفاضلية:
ع َ= س+ ع التي تحقق الشرط ع (0) =1 عند النقطة س = 0.1 يؤخذ:
ويطبق دستور أولر فتنتج القيم التالية:
ع (0.02) = 1.02
ع (0.04) = 1.0408
ع (0.06) = 1.0624
ع (0.08) = 1.0848
ع (0.1) = 1.1081
وتكون القيمة العظمى للخطأ المرتكب هي:
دعد الحسيني
numerical calculation - Calcul numérique
الحساب العددي
تعريف الحساب العددي وأهميته
الحساب العددي هو مجموعة طرائق تؤدي إلى حلول عددية لعددٍ من المسائل. فالتطور العملي والتقني الهائل وجّه الأنظار إلى أن عدداً كبيراً من المسائل العلمية، الرياضية والفيزيائية والهندسية، يتعذر إيجاد حلول عملية لها بالطرائق التحليلية، مما دفع العلماء إلى البحث عن طرائق عددية لحل تلك المسائل وتطوير تلك الطرائق وبرمجتها بحيث يستفاد من القدرة الهائلة للحواسيب، الأمر الذي جعل علم الحساب العددي في مقدمة العلوم التطبيقية الحديثة.
ولعل أهم المسائل التي يعالجها هذا العلم
حل المعادلات الجبرية - إيجاد مجموع متسلسلة عددية[ر] - إيجاد قيم تكامل محدَّد[ر] - حساب مشتق دالة عند نقط معيّنة - إيجاد حل معادلة تفاضلية عادية أو جزئية عند نقط معيّنة - حل مجموعة معادلات خطية... إضافة إلى إعطاء الخوارزميات[ر] ووضع البرامج اللازمة لحل تلك المسائل وتقدير الأخطاء المرتكبة.
المصادر الرئيسة للأخطاء
تتضمن كل مسألة من مسائل الحساب العددي معطيات أولية وخوارزميات ونتائج عددية، ويندر أن تكون قيم المعطيات الأولية معلومة بدقة تامة لأنها إما أن تنتج عن قياسات تقرييية لا تخلو من الخطأ، أو عن قوانين وصيغ تقريبية، أو أنها تحتوي على ثوابت يتعذر تحديد قيمها الدقيقة كالعدد π أو e مثلاً.
وكذلك فإن الخوارزميات وطرائق إيجاد الحلول العددية تضيف أخطاءً جديدة سرعان ما تتراكم بسبب تكرار العمليات الحسابية، كما أن النتائج العددية غالباً ما تكون كسرية غير منتهية ولا يمكن التعبير عنها بعدد منته من الأرقام، الأمر الذي يدعو إلى تدوير الأعداد والاكتفاء بعدد من الأرقام يناسب طول جملة الحاسوب، وقد اصطلح على إجراء التدوير بالشكل التالي:
ننظر إلى أول الأرقام المحذوفة (الرقم الأيسر منها)، فإن كان أكبر من 5، أضفنا إلى آخر رقم غير محذوف واحداً، أما إذا كان أول الأرقام المحذوفة أصغر من 5 حافظنا على الأرقام غير المحذوفة دون تغيير، فالعدد 3.75243 يمكن أن يُدوَّر إلى 3.75 والعدد 3.7572 يمكن أن يدوَّر إلى 3.76. أما إذا كان أول الأرقام المحذوفة 5، فإن كان على يمينه أرقام أخرى أضفنا إلى آخر رقم غير محذوف واحداً. وإذا لم يكن على يمينه أرقام أخرى فإننا ندوِّر العدد بحيث يصبح آخر رقم غير محذوف زوجياً فالعدد 3.6752 يمكن أن يدور إلى 3.68 والعدد 3.635 إلى 3.64 والعدد 3.625 إلى 3.62.
الخطأ المطلق
يستدل مما سبق على أنه من الضروري في كثير من الأحيان اعتماد قيمة تقريبية ب عوضاً عن القيمة الدقيقة لعدد ما س0 يسمى الفرق |ب-س| بين القيمة الدقيقة والقيمة التقريبية بالخطأ المطلق، وتحسب عادة قيمة عظمى لهذا الخطأ يرمز لها بـ Î وهي تحدِّد مقدار الدقة في حساب العدد س، فلو وجد مثلاً أن القيمة التقريبية لجذرٍ للمعادلة س3 – س - 1 = 0 هي س = 1.3247 وأن القيمة العظمى للخطأ المرتكب تساوي 5 × 10-5 فإن هذا يعني أن القيمة الدقيقة للجذر س1 محصورة في الفترة (مجال): 1.32465 < س1 < 1.32475
وإذا قيل إن العدد ب = 1.57 مدوَّر، فإن هذا يعني أن القيمة الدقيقة تقع في الفترة 1.565 ³ ب ³ 1.575.
الحساب التقريبي لجذر معادلة
1- طريقة تنصيف الفترة:
إذا كانت الدالة تا(س) مستمرة على الفترة (المجال) [ب،جـ] وتحقق الشرط:
تا(ب) . تا(جـ) < 0 كان للمعادلة تا(س) =0 جذر في الفترة [ب،جـ]. تعتبر القيمة:
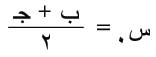
قيمة تقريبية لهذا الجذر، وبحسب المقدار تا (س0)، فإذا تحقق الشرط تا(س0) . تا(ب) <0، كان للمعادلة جذر في الفترة [ب،س0]. تعتبر القيمة:
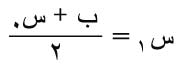
قيمة تقريبية جديدة للجذر، وهكذا تنصف الفترة [بن، جـن] الحاوية على الجذر في كل مرة، ويكتب دستور حساب القيمة التقريبية للجذر على النحو التالي:
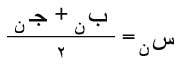
وتكون القيمة العظمى للخطأ المرتكب:
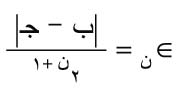
2- طريقة نيوتن:
إذا كانت الدالة تا(س) مُعرّفة على الفترة [ب، جـ] وإذا كان المشتقان الأول والثاني لها مُعرفين على الفترة السابقة وتاَ(س) ≠ 0 و تاً(س)≠ 0 " س ' [ب، جـ] فإن القيمة التقريبية لجذر المعادلة تا(س) =0 تحسب من الدستور:
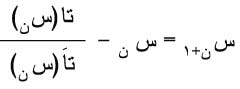
بدءاً من قيمة ابتدائية س0 وتتعين القيمة العظمى للخطأ المرتكب من العلاقة:
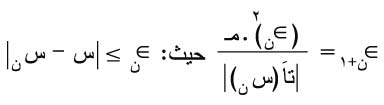
وَ مـ هي قيمة عظمى لـ |تاً(س)| في الفترة [ب، حـ].
مثال: للبحث عن جذر للمعادلة س3 – س – 1 = 0 يلاحظ أن تا(1). تا(2) = - 5 مما يدل على أن لها جذراً في الفترة [2،1] تطبق طريقة تنصيف الفترة لتعيين هذا الجذر فتنتج القيم:
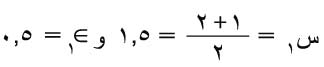
وتا(1) . تا(1.5)<0
............................................................................................. .....................
...........................................
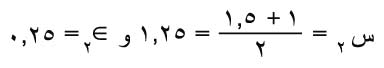
س20 = 1.3247175 ويكون تا(س20) = -1.8×10-6
أما إذا طبقت طريقة نيوتن لتعيين هذا الجذر فإن النتائج تكون بفرض س0 = 1 على النحو: س1 = 1.5، س2 = 1.3478261، س4 = 1.3247181
ويكون تا(س4) 9×10-7، مما يدل على أن النتيجة تقترب من الحل الدقيق حسب هذه الطريقة بسرعة كبيرة.
الحساب التقريبي لمجموع متسلسلة عددية[ر]:
إن المجموع مج لمتسلسلة عددية متقاربة ذات حدود موجبة يكتب على النحو: مج = مجن + قن حيث مجن هو المجموع الجزئي للحدود ن الأولى من المتسلسلة وقن الباقي الذي يسعى إلى الصفر عندما ن ¬ ¥ إذا كانت المتسلسلة متقاربة.
لا يمكن حساب المجموع مج بدقة تامة في كثير من الحالات، لذا تعتبر القيمة مجن قيمة تقريبية لهذا المجموع، ويكون الخطأ المرتكب عندها يساوي قن، ولما كان حساب قن بدوره غير ممكن لذا تحسب قيمة عظمى لهذا الباقي ويتم ذلك كما يلي:
1- معيار كوشي Cauchy: إذا وجد عدد صحيح ط، بحيث أنه أياّ كان:
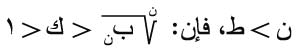
فإن المتسلسلة ذات الحد العام بن تكون متقاربة، وتحسب القيمة العظمى للباقي ن من العلاقة:
2- معيار دالمبير D’alambert: إذا وجد عدد طبيعي ط بحيث أنه أياً كان:
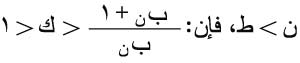
فعندئذٍ تحسب القيمة العظمى للباقي من العلاقة:
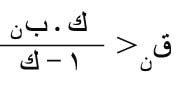
3- إذا كانت المتسلسلة ذات الحد العام بن متناوبة فإن القيمة العظمى للباقي قن تحسب من العبارة:
|قن|<|بن+1|
أما من الناحية العملية فلحساب مجموع متسلسلة بخطأ لايتجاوز
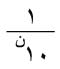، يُحسب مجموع عدد من الحدود الأولى تسبق الحد الذي تنعدم فيه ن + 2 من الأرقام العشرية الأولى وليكن عدد هذه الحدود ط، ويراعى خلال الحساب أن تكون الدقة في حساب قيمة كل من الحدود تفوق 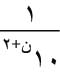فيصبح الخطأ الكلي المرتكب: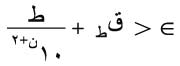وتكون النتيجة على الغالب في حدود الدقة المطلوبة، فإن لم يتحقق ذلك أضيف إلى المجموع الجزئي مجط عدد مناسب من الحدود.
مثال: تحسب قيمة تقريبية لـ
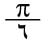بخطأ لايتجاوز 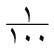من المتسلسلة: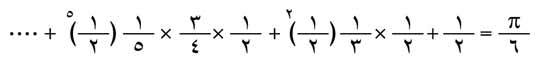يكتفى بثلاثة حدود فينتج
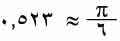. وتكون القيمة العظمى للخطأ 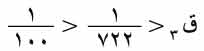.الحساب التقريبي لتكامل محدَّد[ر]:
1- طريقة النشر بمتسلسلة: لحساب قيمة التكامل المحدَّد :
تُنْشر الدالة تا(س) في متسلسلة صحيحة تحوي فترة تقاربها الفترة [ب، جـ] فيكون:
تا(س) = د0+ د1س+ د2س2+...+ دنسن+...
تُكامل المتسلسلة الناتجة حداً حداً فينتج:
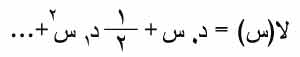
وتكون قيمة التكامل المطلوبة هي:
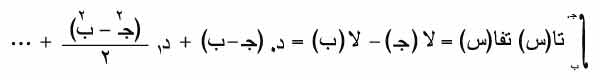
ويتم المطلوب بحساب مجموع المتسلسلة الناتجة بشكل تقريبي.
2- طريقة أشباه المنحرف: تقسم الفترة [ب، جـ] إلى فترات جزئية متساوية عددها ن ويقام من نقط التقسيم س0=ب،س1،....سن=جـ مستقيمات تعامد محور السينات إن طول كل فترة جزئية
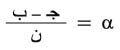يحسب مجموع سطوح أشباه المنحرف الناتجة عن استبدال أوتار أقواس المنحني بيان الدالة تا(س) في الفترات الجزئية بهذه الأقواس ويعتبر هذا المجموع قيمة تقريبية للتكامل المحدد ويكتب: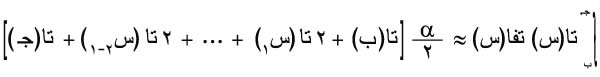وتحسب القيمة العظمى للخطأ المرتكب من العلاقة:
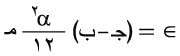
حيث مـ هي قيمة عظمى لـ | تاً(س)| في الفترة [ب، جـ].
وتزداد دقة الحساب بزيادة عدد الفترات الجزئية.
مثال: لحساب التكامل المحدد
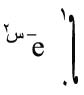يطبق دستور أشباه المنحرف بفرض: | a | = | 0.1 |
تحسب القيمة العظمى للخطأ فتكون:
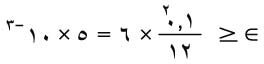
حساب مشتق دالة عند نقطة معينة بشكل تقريبي:
طريقة تايلور Taylor: لتعيين مشتق الدالة تا(س) عند نقطة س0 معينة تنشر الدالة في متسلسلة صحيحة بجوار س0 ويكتفى بثلاثة حدود فقط فيكون:
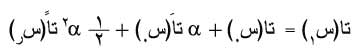
حيث:
س1- س0 = a، س0< سر< س1
ويحسب تاَ(س0) فيكون:
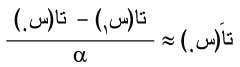
وتكون القيمة العظمى للخطأ:
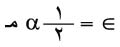
بفرض مـ هي القيمة العظمى لـ |تاً(س)| .
إيجاد حل معادلة تفاضلية عند نقطة معينة بشكل تقريبي:
طريقة أولر Euler: لإيجاد حل المعادلة التفاضلية:
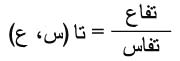
التي تحقق الشرط ع = ع0 عندما س = س0 عند النقطة (سن+1، عن+1) تنشر الدالة ع (س) بجوار سن وتكتب العلاقة:
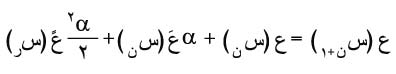
حيث:
a = سن+1 – سن، سن ³ سر ³ سن+1
ويكتب دستور أولر على النحو:
ع(سن+1) = ع(سن) + a تا(سن،عن)
وتكون القيمة العظمى للخطأ المرتكب:
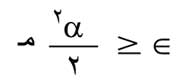
وذلك بفرض أن مـ قيمة عظمى لـ | عً (س)|
يطبق الدستور السابق بصورة مكررة توخياً للدقة.
مثال: لإيجاد حل المعادلة التفاضلية:
ع َ= س+ ع التي تحقق الشرط ع (0) =1 عند النقطة س = 0.1 يؤخذ:
| a | = | 0.02 |
ع (0.02) = 1.02
ع (0.04) = 1.0408
ع (0.06) = 1.0624
ع (0.08) = 1.0848
ع (0.1) = 1.1081
وتكون القيمة العظمى للخطأ المرتكب هي:
| Î | = | 0.002 |