تحفيظ جدول الضرب للطفل بطريقة سهلة وسريعة

لطالما شكل تحفيظ جدول الضرب للأولاد، والذي يعد مهارة أساسية يجب على الطفل اكتسابها في مراحل دراسته الأولى، تحدياً بالنسبة للأهل لذلك هم في سعي دائم لإيجاد طرق سهلة تساعد أطفالهم في حفظه وإلا سيعانون في دراستهم اللاحقة عندما يضطرون لضرب أرقام صعبة، لذلك يجب عند تعليمه الاعتماد على بعض الطرق التي تسهل العملية.
أهمية تعليم جدول الضرب للطفل
يشكل جدول الضرب حجر الأساس في الرياضيات لذلك يُعتبر تعلمه مهارةً هامة يجب اكتسابها، وهي عملية بسيطة إذا ما علمنا أن معرفة الجداول الأساسية في الضرب تُسهل على الطفل تعلم باقي الجداول، فمثلاً معرفة الطفل لجدول الضرب بالعدد 2 سيعلمه أن جدول الضرب في 4 هو مضاعفات نواتج جدول 2، كما أنها تجهز الطفل لتلقي أساسيات جديدة في الرياضيات كالكسور والقسمة والنسبة المئوية، أما الأهم هو أنَّ تمكُّن الطفل من حفظه سيعطيه ثقة بقدراته على استيعاب الرياضيات ولن يضطر إلى استخدام أصابعه في إيجاد نواتج العمليات الحسابية.
طرق فعالة لتحفيظ جدول الضّرب للطفل
بعض الحيل لحفظ جدول الضرب
إليك أيضًا هذا الفيديو التعليمي لتحفيظ جدول الضرب بسهولة:

حفظ جدول الضرب للاطفال
يُعدّ تعليم جدول الضرب للأطفال من أهمّ المشاكل التي يعاني منها الوالدان قبل الأطفال أنفسهم، وقبل كلّ شيءٍ علينا أن نعلم أن أجمل ما في الرياضيات هو المرونة التي تتمتع بها الأرقام وهو ما يطلق عليه بـ "إحساس الرقم"، لذلك وعلى الرّغم من أهمية الحقائق الرياضية في جدول الضرب إلّا أنّ التركيز على الحفظ التكراري دون التفاعل مع الأرقام يعدّ المثبط الأكبر للمهارات الذهنية الإبداعية عند الطفل، ممّا يحول اهتمام الطفل عن الرياضيات الذي يختلف عن غيره من المواد التي يدرسها الطالب في مدرسته كاللغة الأجنبية.
الطالب الذي يعتمد على ذاكرته فقط في جدول الضرب سيقع في معضلة النسيان التي يعاني منها أيّ دماغٍ طبيعيٍّ، فعلى سبيل المثال قد ينسى الطالب جداء 7×8 ولكن الطالب المتمرّن سيعلم أنها مجرد إضافة سبعة إلى حاصل جداء 7×7 أي 49+7 وهو 56.
ولتعليم أطفالكم حفظ جدول الضرب بطريقةٍ بسيطةٍ وسهلةٍ فهناك عدّة خطواتٍ لا بدّ من اتباعها:
ربط الضرب بعملية الجمع
من بديهيات جدول الضرب هو ربطه بعملية الجمع لمعرفة أساس العملية، وهو إضافةٌ متكرّرةٌ للرقم للحصول على مضاعفات العدد، على سبيل المثال العملية 4 × 3 هي جمع الرقم 4 مع نفسه لثلاث مرّات، أي:
4×3=4 +4 +4 =12
البدء بأسهل الجداول وهو جدول الضرب للعددين(0-1)
الضرب بـ 0
وفقًا لخاصيّة الإضافة فإنّ إضافة العدد صفر لأيّ رقمٍ لا يمثّل أيّ إضافةٍ، كما أنّ ضرب العدد صفر بأيّ رقمٍ يعني تكراره صفر مرّة؛ أي دون تكرار له، وبالتالي ضرب أيّ رقمٍ بالعدد صفر يساوي للصفر، مثال: 5×0= 0
ومن الممكن ربط الخاصية ببعض الأمثلة لتوضيح الفكرة للطفل، فصحنٌ يحوي خمس حبّات تفاحٍ يحوي صفرًا من الموز، أي تكرار أو عدد قرون الموز في صحن التفاح هو صفر.
الضرب بالرقم 1
وهو ما يُطلق عليه بخاصّية الهوية أو التعريف، لأن ناتج ضرب أي رقم بالعدد واحد هو الرقم نفسه، وفقًا لخاصية الإضافة أو الجمع، فالضرب بالعدد واحد يعني تكرار الرقم لمرة واحدة، أي: 2×1=2
ومن الممكن تجسيد الفكرة في مثالٍ واقعيٍّ، كما في عدد أيام الأسبوع في صفٍّ واحدٍ ضمن التقويم وهو سبعة أيام في أسبوعٍ واحد.
تغطية كامل جدول الضرب

أهميّة خاصية التبديل في تسهيل عملية الضرب
كما الجمع، يُعدّ الضرب عمليةً تبادليةً، وبالتالي لن تختلف قيمة الناتج في حال عكس القيم المتفاعلة، على سبيل المثال:
4×3=3×4=12
4+4+4=3+3+3+3=12
وبالتالي فإن نصف البيانات في المخطط مكررّةً، ممّا يحفّز الأطفال على تعلم ما تبقى من البيانات.

تعلم مضاعفات الأعداد
الخطوة الأخيرة المساعدة هي بتعلم الحصول على مضاعفات كلّ رقمٍ وفقًا لخاصية الإضافة، وبالتالي تكون قد حصلت على مخططٍ كامل البيانات لجدول الضرب من 1 حتى 10.
أفضل الطرق لحفظ جدول الضرب
أصبح طفلك الآن في السادسة من عمره، وهو مستعدٌ للقيام بعملية الضرب الرياضية، بعد تركيز مفهوم الأرقام بشكلٍ تصويريٍّ وتجريديٍّ وملموس في ذهنه، وبعد توضيح أهمية الرياضيات في حياتنا اليومية ومقارنتها بأمثلةٍ واقعيةٍ بشكلٍ دائمٍ.
ولفهم عملية الضرب لا بدّ من فهم محتواها المرتبط بعملية الجمع، وبخصائص العملية التبادلية، ممّا يمكنهم من حفظ جدول الضرب بطرقٍ إستنتاجيةٍ، ليبقى في ذاكرتهم على مدى الحياة، ومن الأساليب الممكن إتباعها لتوضيح عملية الضرب ما يلي:
النمذجة الشريطية
هي عمليةٌ تصويريةٌ للأرقام لتوضيح ما تعنيه، باستخدام أشرطةٍ مقسّمةٍ إلى مستطيلاتٍ، على سبيل المثال إليك العملية الحسابية التالية: 2×3=2+2+2
فالمستطيل الواحد يحمل قيمة الرقم 2، ومنه يمكن تمثيل العملية السابقة بثلاث مستطيلات تحمل قيمة الرقم 2، وبالتالي: 2×3=2+2+2=6

كذلك توضح لنا النمذجة الشريطية مفهوم التبادلية في الضرب، فالنتيجة لا تتغيرلأن:
2×3=3+3=6
2×3=2+2+2=6
وهو ما يختلف كليًّا في عملية القسمة فهي لبست تبادلية، ففي المثال السابق:
6 ÷ 2 = 3
2 ÷ 6 = 0.33333333333
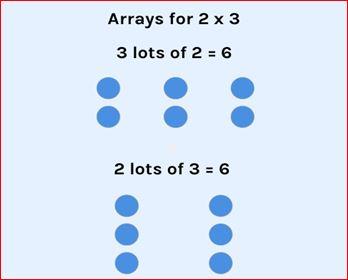
المصفوفات
هي تصويرٌ حيٌّ لجدول الضرب، ممّا يوصل فكرة العملية الحسابية إلى ذهن الطفل بشكلٍ تصويريٍّ، تعتمد على توضيح الأرقام على شكل مجموعاتٍ أو حصصٍ، ففي المثال السابق، 3×2 هي ثلاث مجموعات من ثنائيات، أو يمكن صياغتها بطريقة مختلفة؛ 2×3 هي مجموعتان من ثلاثة نقاط، والنتيجة واحدة، فيمكن تمثيل الرقم 6 في عدة مصفوفات أو مجموعات.
الضرب باستخدام مستقيم الأعداد
تطبيقًا لعملية الجمع خلال الضرب، فإنّ مستقيم الأعداد من أوضح الطرق لإيصال فكرة التخطي أو القفز، فهو القيام بتنقلاتٍ على مستقيم الأعداد بحجم عددٍ، وبعدد المجموعات، فهو تمثيل واضح للانتقال بين المضاعفات بالجمع بالعدد ذاته، على سبيل المثال: 3×4
هو عدد ثلاث مجموعات من أربعة كائنات، فبعد رسم مستقيم الأعداد نبدأ من النقطة صفر للانطلاق في ثلاث قفزات، وكلّ قفزةٍ بالحجم 4، كما يلي:
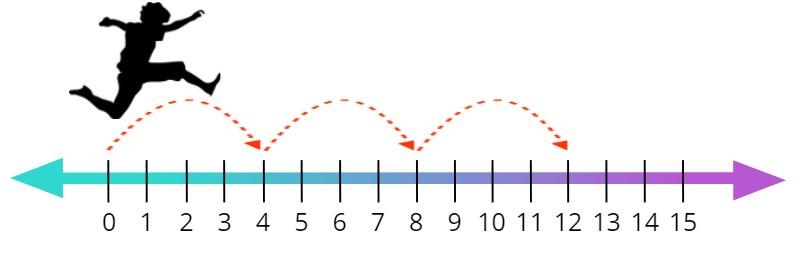
وبذلك نصل إلى النتيجة المطلوبة 12 بالانتقال بين مضاعفات العدد 4: 4-8-12، بإضافة 4 في كل قفزة.
في مثال آخر، لحساب 5×2 علينا بالقفز خمس مرات وكل قفزة بحجم الرقم 2، وبذلك ننتقل بين مضاعفات العدد 2 بإضافة 2 في كل قفزة حتى نصل إلى النتيجة الصحيحة: 2_4_6_8_10.
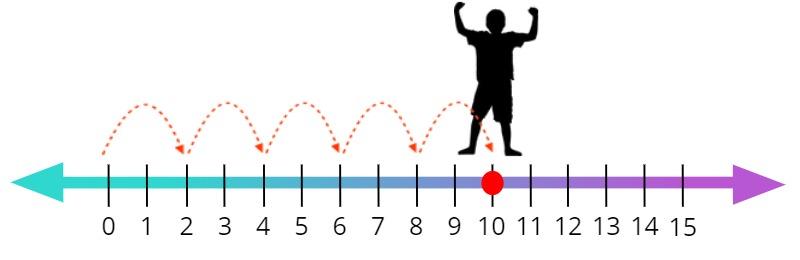
وبذلك نصل إلى الرقم 10.
تمارين جدول الضرب
أفضل وسيلةٍ لإيصال مفهوم جدول الضرب للطفل هي بمعرفة أهميته والغاية منه، عبر بعض الأمثلة الحياتية اليومية، وإليك بعض التمارين الواقعية:
كم عدد البيض لدجاجة تبيض بيضتان في كلَ يوم على مدى ثلاثة أيام؟
هنا يمكن حساب عدد البيض المقسّم على ثلاث مجموعاتٍ وهي الأيام الثلاثة، بضرب عدد البيضات في اليوم الواحد بعدد الأيام:

تحتوي الحقيبة الوحدة على خمس كعكات وبالتالي العدد الكلي هو ناتج ضرب عدد الكعكات بالحقيبة الواحدة بعدد الحقائب: 5×2=5+5= 10
ستدفع 6 بنسات لكلّ حقيبةٍ من الحقائب الربعة فالثمن هو ناتج جمع 6 لأربع مرات، أي الوصول لمضاعفات الرقم 6 أربع مرات: 6×4 =6+6+6+6= 24
عليك أن تدفع 10 جنيه ثلاث مرات لعلب الجبنة الثلاث، أي: 10×3= 10+10+10= 30
جدول الضرب كامل بالعربي من 1 إلى 12
جدول ضرب 1
جدول ضرب العدد 2
جدول ضرب العدد 3
جدول ضرب العدد 4
جدول ضرب العدد 5
جدول ضرب العدد 6
جدول ضرب العدد 7
جدول ضرب العدد 8
جدول ضرب العدد 9
جدول ضرب العدد 10
جدول ضرب 11
جدول ضرب 12
لطالما شكل تحفيظ جدول الضرب للأولاد، والذي يعد مهارة أساسية يجب على الطفل اكتسابها في مراحل دراسته الأولى، تحدياً بالنسبة للأهل لذلك هم في سعي دائم لإيجاد طرق سهلة تساعد أطفالهم في حفظه وإلا سيعانون في دراستهم اللاحقة عندما يضطرون لضرب أرقام صعبة، لذلك يجب عند تعليمه الاعتماد على بعض الطرق التي تسهل العملية.
أهمية تعليم جدول الضرب للطفل
يشكل جدول الضرب حجر الأساس في الرياضيات لذلك يُعتبر تعلمه مهارةً هامة يجب اكتسابها، وهي عملية بسيطة إذا ما علمنا أن معرفة الجداول الأساسية في الضرب تُسهل على الطفل تعلم باقي الجداول، فمثلاً معرفة الطفل لجدول الضرب بالعدد 2 سيعلمه أن جدول الضرب في 4 هو مضاعفات نواتج جدول 2، كما أنها تجهز الطفل لتلقي أساسيات جديدة في الرياضيات كالكسور والقسمة والنسبة المئوية، أما الأهم هو أنَّ تمكُّن الطفل من حفظه سيعطيه ثقة بقدراته على استيعاب الرياضيات ولن يضطر إلى استخدام أصابعه في إيجاد نواتج العمليات الحسابية.
طرق فعالة لتحفيظ جدول الضّرب للطفل
- إحدى الطرق القديمة الفعالة هي أن يقوم الأهل بتحضير ورقة جداول ضرب فارغة يقومون بملئها مع أطفالهم وعند اكتمالها يقومون بوضعها في مكان يراه الطفل بشكل دائم كباب غرفته أو خزانته ثم يقومون بمراجعته يومياً قبل العشاء مثلاً لكن دون أي ضغط على الطفل، والقاعدة الأساسية هنا هي أنهم كلما تمرنوا أكثر كلما تعلموه بشكلٍ أفضل.
- التأكد من تعلمهم القواعد الأساسية والسهلة أولاً، فالبدء بتعليم الطفل جداول ضرب سهلة كجدول ضرب الأعداد بـ 2 أو 10 وترك جداول الضرب الصعبة إلى أن يكتسب المهارات الأساسية السهلة يعطيه الثقة بقدرته على حفظ جداول الضرب.
- تعليم الأطفال بعض الحيل في جدول الضرب، فمثلاً عند تعليم جدول الضرب بـ 9 يمكن تعليم الطفل حيلة اليدين فعليه أن يرفع أصابعه العشرة وعندما يريد ناتج 1×9 عليه أن يُخفِض خنصر يده اليسرى ليكون الناتج هو عدد الأصابع المتبقية أي 9، ولإيجاد ناتج 2×9 عليه أن يُخفض البنصر الأيسر ليكون الناتج هو إصبع واحد يليه فراغ يليه ثمانية أصابع أي 18، وهكذا يسير الأمر حتى 9×9.
- يمكن استخدام مواقع متخصصة على الانترنت كموقع A Plus Math التعليمي والذي يقدم طريقة مراجعة تفاعلية فبمجرد أن يكتب الطالب إجابة المسائل المطروحة يتلقى تعقيباً عليه.
- توظيف الموسيقى في العملية التعليمية فموقع Songs For Teaching.com مثلاً يقدم مجموعة من الأغاني ذات الألحان الجذابة، ويمكن الاستماع إلى بعض الألحان مجاناً أو تعليم الأطفال الجدول وربطه بألحان أغانٍ مألوفة لهم.
بعض الحيل لحفظ جدول الضرب
- أفضل الخدع هي معرفة التوائم في جدول الضرب أي أن ناتج 2×8 هو نفسه 8×2، أي وفق هذه القاعدة سيحفظ الطفل نصف جدول الضرب فقط.
- تعليم الطفل خدع الأعداد:
- جدول الضرب بالعدد 2 هو عبارة عن جمع الرقم مع نفسه أو مضاعفته أي 9×2 هو نفسه 9+9.
- جدول الضرب بالعدد 4 هو مضاعفة الرقم ثم مضاعفة الناتج مجدداً مثل 9×4 هو 18=9×2 ثم 36=18×2.
- جدول الضرب بالعدد 5 هو أخذ نصف العدد المضروب بـ5 ثم ضربه بـ10 فمثلاً 6×5 هو 30=10×3 (حيث 3 هو نصف العدد 6)، ويمكن ضرب العدد 6بـ10 ليكون ناتج 6×5 هو نصف ناتج 6×10 أي 30.
- في جدول الضرب بالعدد 6، عند ضرب عدد زوجي بـ6 ستكون مرتبة الآحاد في الناتج هي الرقم الزوجي نفسه، كما في 12=2×6 و 24=4×6 و 36=6×6
- لحفظ ناتج 56=7×8 يجب تذكر ترتيب الأرقام 5،6،7،8 (8×7=56).
- قاعدة حفظ جدول العدد 8 هي: ضاعف ضاعف ضاعف أي: 6×8 هي 12=6×2 ثم 24=12×2 ثم 48=24×2.
- لتسهيل الضرب بالعدد 9 توجد عدة طرق:
- نقوم بضرب الرقم بالعدد 10 ثم نطرحه من الناتج كما في 54=6×9 هي نفسها 6-6×10 أي 54=6-60
- آحاد نواتج ضرب الأرقام من 1 إلى 10 بالرقم 9 هي بالترتيب 6،7،8،9،..الخ أي 9=1×9 و18=2×9 و27=3×9 وهكذا، أما عشرات نواتج ضرب الأرقام من 1 إلى 10 بالرقم 9 هي بالترتيب 3،2،1،0،...الخ أي 09=1×9 و 18 =2×9 و27 =3×9 وهكذا.
- طرح واحد من الرقم المضروب يعطي رقم العشرات للناتج ويكون الآحاد هو ناتج طرح 9 من رقم العشرات كما في المثال التالي 45=5×9، حيث رقم العشرات هو ناتج 4=1-5 والآحاد هو ناتج 5=4-9.
- يمكن أيضاً استخدام خدعة اليد التي ذُكرت سابقاً.
- لضرب الأرقام ب10 نضيف صفراً إلى يمين الرقم فقط أي 20 =2×10.
- لضرب رقم ما بـ11 نكتب الرقم في الناتج مرتين أي 99=9×11، أما لضرب الأعداد من 10 إلى 18 بـ11 يكون بوضع ناتج جمع رقمي الآحاد والعشرات للعدد المضروب وتوسيطه بين آحاده وعشراته مثل 165=15×11 حيث الرقم 6 هو ناتج 5+1، وفي حال كان ناتج جمعهما أكبر من 9 نقوم بإضافة الواحد لعشرات العدد المضروب أي لإيجاد ناتج 75×11 نجمع 12=7+5 نضع الرقم 2 بين آحاد وعشرات العدد ( أي بين 5 و7) ونضيف 1 إلى عشراته (أي إلى 7) فيصبح الناتج 825.
- للضرب بـ12 نقسم 12 إلى 10 و2 حيث يُضرب الرقم بـ10 ويُجمع مع ناتج ضربه بـ2 مثل 4×12 يمكن تجزئته إلى 10×4+2×4 أي 48=40+8، ونفس الطريقة تطبق عند الضرب بـ15.
- للضرب بـ20 نضرب الرقم بـ10 ثم نضاعفه كما في 4×20 هي 4*10=40 حيث 40 هي حاصل ضرب 4 بـ10 ثم نضاعف الناتج: 40*2=80.
إليك أيضًا هذا الفيديو التعليمي لتحفيظ جدول الضرب بسهولة:
حفظ جدول الضرب للاطفال
يُعدّ تعليم جدول الضرب للأطفال من أهمّ المشاكل التي يعاني منها الوالدان قبل الأطفال أنفسهم، وقبل كلّ شيءٍ علينا أن نعلم أن أجمل ما في الرياضيات هو المرونة التي تتمتع بها الأرقام وهو ما يطلق عليه بـ "إحساس الرقم"، لذلك وعلى الرّغم من أهمية الحقائق الرياضية في جدول الضرب إلّا أنّ التركيز على الحفظ التكراري دون التفاعل مع الأرقام يعدّ المثبط الأكبر للمهارات الذهنية الإبداعية عند الطفل، ممّا يحول اهتمام الطفل عن الرياضيات الذي يختلف عن غيره من المواد التي يدرسها الطالب في مدرسته كاللغة الأجنبية.
الطالب الذي يعتمد على ذاكرته فقط في جدول الضرب سيقع في معضلة النسيان التي يعاني منها أيّ دماغٍ طبيعيٍّ، فعلى سبيل المثال قد ينسى الطالب جداء 7×8 ولكن الطالب المتمرّن سيعلم أنها مجرد إضافة سبعة إلى حاصل جداء 7×7 أي 49+7 وهو 56.
ولتعليم أطفالكم حفظ جدول الضرب بطريقةٍ بسيطةٍ وسهلةٍ فهناك عدّة خطواتٍ لا بدّ من اتباعها:
ربط الضرب بعملية الجمع
من بديهيات جدول الضرب هو ربطه بعملية الجمع لمعرفة أساس العملية، وهو إضافةٌ متكرّرةٌ للرقم للحصول على مضاعفات العدد، على سبيل المثال العملية 4 × 3 هي جمع الرقم 4 مع نفسه لثلاث مرّات، أي:
4×3=4 +4 +4 =12
البدء بأسهل الجداول وهو جدول الضرب للعددين(0-1)
الضرب بـ 0
وفقًا لخاصيّة الإضافة فإنّ إضافة العدد صفر لأيّ رقمٍ لا يمثّل أيّ إضافةٍ، كما أنّ ضرب العدد صفر بأيّ رقمٍ يعني تكراره صفر مرّة؛ أي دون تكرار له، وبالتالي ضرب أيّ رقمٍ بالعدد صفر يساوي للصفر، مثال: 5×0= 0
ومن الممكن ربط الخاصية ببعض الأمثلة لتوضيح الفكرة للطفل، فصحنٌ يحوي خمس حبّات تفاحٍ يحوي صفرًا من الموز، أي تكرار أو عدد قرون الموز في صحن التفاح هو صفر.
الضرب بالرقم 1
وهو ما يُطلق عليه بخاصّية الهوية أو التعريف، لأن ناتج ضرب أي رقم بالعدد واحد هو الرقم نفسه، وفقًا لخاصية الإضافة أو الجمع، فالضرب بالعدد واحد يعني تكرار الرقم لمرة واحدة، أي: 2×1=2
ومن الممكن تجسيد الفكرة في مثالٍ واقعيٍّ، كما في عدد أيام الأسبوع في صفٍّ واحدٍ ضمن التقويم وهو سبعة أيام في أسبوعٍ واحد.
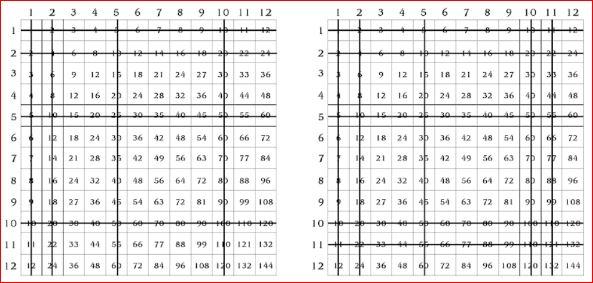
تغطية كامل جدول الضرب
- قم بإنشاء مخططٍ أو رسمٍ بياني لجدول الضرب 10×10.
- تعليم الطالب حول كيفية تتبع البيانات على الجدول باستخدام المحورين الأفقي والعمودي.
- الآن يمكنك اتباع الحيل السابقة الذكر للعثور على أنماطٍ محددّةٍ في المخطط، كما في جدول الرقم عشرة والذي تنتهي جميع نواتجه بالصفر.
- الآن يمكنك حذف نتائج الجداول السهلة كجدول الرقم واحد والعشرة، والبعض يجد نفس السهولة في حفظ واستنتاج جدول العدد 2 أو 5 ، وباستمرار حذفك للبيانات التي أصبحت واضحةً ومعروفةً لديك ستقلّ كمية البيانات المتبقية لتتعلمها.
أهميّة خاصية التبديل في تسهيل عملية الضرب
كما الجمع، يُعدّ الضرب عمليةً تبادليةً، وبالتالي لن تختلف قيمة الناتج في حال عكس القيم المتفاعلة، على سبيل المثال:
4×3=3×4=12
4+4+4=3+3+3+3=12
وبالتالي فإن نصف البيانات في المخطط مكررّةً، ممّا يحفّز الأطفال على تعلم ما تبقى من البيانات.
تعلم مضاعفات الأعداد
الخطوة الأخيرة المساعدة هي بتعلم الحصول على مضاعفات كلّ رقمٍ وفقًا لخاصية الإضافة، وبالتالي تكون قد حصلت على مخططٍ كامل البيانات لجدول الضرب من 1 حتى 10.
أفضل الطرق لحفظ جدول الضرب
أصبح طفلك الآن في السادسة من عمره، وهو مستعدٌ للقيام بعملية الضرب الرياضية، بعد تركيز مفهوم الأرقام بشكلٍ تصويريٍّ وتجريديٍّ وملموس في ذهنه، وبعد توضيح أهمية الرياضيات في حياتنا اليومية ومقارنتها بأمثلةٍ واقعيةٍ بشكلٍ دائمٍ.
ولفهم عملية الضرب لا بدّ من فهم محتواها المرتبط بعملية الجمع، وبخصائص العملية التبادلية، ممّا يمكنهم من حفظ جدول الضرب بطرقٍ إستنتاجيةٍ، ليبقى في ذاكرتهم على مدى الحياة، ومن الأساليب الممكن إتباعها لتوضيح عملية الضرب ما يلي:
النمذجة الشريطية
هي عمليةٌ تصويريةٌ للأرقام لتوضيح ما تعنيه، باستخدام أشرطةٍ مقسّمةٍ إلى مستطيلاتٍ، على سبيل المثال إليك العملية الحسابية التالية: 2×3=2+2+2
فالمستطيل الواحد يحمل قيمة الرقم 2، ومنه يمكن تمثيل العملية السابقة بثلاث مستطيلات تحمل قيمة الرقم 2، وبالتالي: 2×3=2+2+2=6
كذلك توضح لنا النمذجة الشريطية مفهوم التبادلية في الضرب، فالنتيجة لا تتغيرلأن:
2×3=3+3=6
2×3=2+2+2=6
وهو ما يختلف كليًّا في عملية القسمة فهي لبست تبادلية، ففي المثال السابق:
6 ÷ 2 = 3
2 ÷ 6 = 0.33333333333
المصفوفات
هي تصويرٌ حيٌّ لجدول الضرب، ممّا يوصل فكرة العملية الحسابية إلى ذهن الطفل بشكلٍ تصويريٍّ، تعتمد على توضيح الأرقام على شكل مجموعاتٍ أو حصصٍ، ففي المثال السابق، 3×2 هي ثلاث مجموعات من ثنائيات، أو يمكن صياغتها بطريقة مختلفة؛ 2×3 هي مجموعتان من ثلاثة نقاط، والنتيجة واحدة، فيمكن تمثيل الرقم 6 في عدة مصفوفات أو مجموعات.

الضرب باستخدام مستقيم الأعداد
تطبيقًا لعملية الجمع خلال الضرب، فإنّ مستقيم الأعداد من أوضح الطرق لإيصال فكرة التخطي أو القفز، فهو القيام بتنقلاتٍ على مستقيم الأعداد بحجم عددٍ، وبعدد المجموعات، فهو تمثيل واضح للانتقال بين المضاعفات بالجمع بالعدد ذاته، على سبيل المثال: 3×4
هو عدد ثلاث مجموعات من أربعة كائنات، فبعد رسم مستقيم الأعداد نبدأ من النقطة صفر للانطلاق في ثلاث قفزات، وكلّ قفزةٍ بالحجم 4، كما يلي:

وبذلك نصل إلى النتيجة المطلوبة 12 بالانتقال بين مضاعفات العدد 4: 4-8-12، بإضافة 4 في كل قفزة.
في مثال آخر، لحساب 5×2 علينا بالقفز خمس مرات وكل قفزة بحجم الرقم 2، وبذلك ننتقل بين مضاعفات العدد 2 بإضافة 2 في كل قفزة حتى نصل إلى النتيجة الصحيحة: 2_4_6_8_10.

وبذلك نصل إلى الرقم 10.
تمارين جدول الضرب
أفضل وسيلةٍ لإيصال مفهوم جدول الضرب للطفل هي بمعرفة أهميته والغاية منه، عبر بعض الأمثلة الحياتية اليومية، وإليك بعض التمارين الواقعية:
كم عدد البيض لدجاجة تبيض بيضتان في كلَ يوم على مدى ثلاثة أيام؟
هنا يمكن حساب عدد البيض المقسّم على ثلاث مجموعاتٍ وهي الأيام الثلاثة، بضرب عدد البيضات في اليوم الواحد بعدد الأيام:

- كم العدد الإجمالي للكعكات الموجودة في حقيبتين مملوءتين بخمس كعكاتٍ؟
تحتوي الحقيبة الوحدة على خمس كعكات وبالتالي العدد الكلي هو ناتج ضرب عدد الكعكات بالحقيبة الواحدة بعدد الحقائب: 5×2=5+5= 10
- ما ثمن شرائك لأربعة حقائب كلٍّ منها بسعر 6 بنسات؟
ستدفع 6 بنسات لكلّ حقيبةٍ من الحقائب الربعة فالثمن هو ناتج جمع 6 لأربع مرات، أي الوصول لمضاعفات الرقم 6 أربع مرات: 6×4 =6+6+6+6= 24
- ما تكلفة شرائك لثلاث علب جبنة بسعر 10 جنيه للواحدة؟
عليك أن تدفع 10 جنيه ثلاث مرات لعلب الجبنة الثلاث، أي: 10×3= 10+10+10= 30
جدول الضرب كامل بالعربي من 1 إلى 12
جدول ضرب 1
- 1×1=1
- 2×1=2
- 3×1=3
- 4×1=4
- 5×1=5
- 6×1=6
- 7×1=7
- 8×1=8
- 9×1=9
- 10×1=10
- 11×1=11
- 12×1=12
جدول ضرب العدد 2
- 2 ×1 = 2
- 2 × 2= 4
- 2 × 3= 6
- 2 × 4= 8
- 2 × 5= 10
- 2 × 6= 12
- 2 × 7= 14
- 2 × 8= 16
- 2 × 9= 18
- 2×10=20
- 2 × 11= 22
- 2 × 12= 24
جدول ضرب العدد 3
- 3 × 1= 3
- 3 × 2= 6
- 3 × 3= 9
- 3 × 4= 12
- 3 × 5= 15
- 3 × 6= 18
- 3 × 7= 21
- 3 × 8= 24
- 3 ×9 = 27
- 3 ×10 = 30
- 3 ×11 = 33
- 3 ×12 = 36
جدول ضرب العدد 4
- 4 × 1= 4
- 4 × 2= 8
- 4 × 3= 12
- 4 × 4= 16
- 4 × 5= 20
- 4 × 6= 24
- 4 × 7= 28
- 4 × 8= 32
- 4 × 9= 36
- 4 × 10= 40
- 4 × 11= 44
- 4 × 12= 48
جدول ضرب العدد 5
- 5 × 1= 5
- 5 × 2= 10
- 5 × 3= 15
- 5 × 4= 20
- 5 × 5= 25
- 5 × 6 = 30
- 5 × 7= 35
- 5 × 8 =40
- 5 × 9 = 45
- 5 × 10= 50
- 5 × 11= 55
- 5 × 12= 60
جدول ضرب العدد 6
- 6 × 1= 6
- 6 × 2= 12
- 6 × 3= 18
- 6 × 4= 24
- 6 × 6= 36
- 6 × 5= 30
- 6 × 6= 36
- 6 × 7= 42
- 6 × 8 = 48
- 6 × 9 = 54
- 6 × 10 = 60
- 6 × 11 = 66
- 6 × 12 = 72
جدول ضرب العدد 7
- 7 × 1 = 7
- 7 × 2 = 14
- 7 × 3 = 21
- 7 × 4 = 28
- 7 × 5 = 35
- 7 × 6 = 42
- 7 × 7 = 49
- 7 × 8 = 56
- 7 × 9 = 63
- 7 × 10 = 70
- 7 × 11 = 77
- 7 × 12 = 84
جدول ضرب العدد 8
- 8 × 1 = 8
- 8 × 2 = 16
- 8 × 3 = 24
- 8 × 4 = 32
- 8 × 5 = 40
- 8 × 6 = 48
- 8 × 7= 56
- 8 × 8 = 64
- 8 × 9 = 72
- 8 × 10 = 80
- 8 × 11 = 88
- 8 × 12 = 96
جدول ضرب العدد 9
- 9 × 1 = 9
- 9 × 2 = 18
- 9 × 3 = 27
- 9 × 4 = 36
- 9 × 5 = 45
- 9 × 6 = 54
- 9 × 7 = 63
- 9 × 8 = 72
- 9 × 9 = 81
- 9 × 10 = 90
- 9 × 11 = 99
- 9 × 12 = 108
جدول ضرب العدد 10
- 10 × 1 = 10
- 10 × 2 = 20
- 10 × 3 = 30
- 10 × 4 = 40
- 10 × 5 = 50
- 10 × 6 = 60
- 10 × 7 = 70
- 10 × 8 = 80
- 10 × 9 = 90
- 10 × 10 = 100
- 10 × 11= 110
- 10 × 12 = 120
جدول ضرب 11
- 11 × 1 = 11
- 11 × 2 = 22
- 11 × 3 = 33
- 11 × 4 = 44
- 11 × 5 = 55
- 11 × 6 = 66
- 11 × 7 = 77
- 11 × 8 = 88
- 11 × 9 = 99
- 11 × 10 = 110
- 11 × 11 = 121
- 11 × 12 = 132
جدول ضرب 12
- 12 × 1 = 12
- 12 × 2 = 24
- 12 × 3 = 36
- 12 × 4 = 48
- 12 × 5 = 60
- 12 × 6 = 72
- 12 × 7 = 84
- 12 × 8 = 96
- 12 × 9 = 108
- 12 × 10 = 120
- 12 × 11 = 132
- 12 × 12 = 144
- أفضل الخدع هي معرفة التوائم في جدول الضرب أي أن ناتج 2×8 هو نفسه 8×2، أي وفق هذه القاعدة سيحفظ الطفل نصف جدول الضرب فقط.
- تعليم الطفل خدع الأعداد:
- جدول الضرب بالعدد 2 هو عبارة عن جمع الرقم مع نفسه أو مضاعفته أي 9×2 هو نفسه 9+9.
- جدول الضرب بالعدد 4 هو مضاعفة الرقم ثم مضاعفة الناتج مجدداً مثل 9×4 هو 18=9×2 ثم 36=18×2.
- جدول الضرب بالعدد 5 هو أخذ نصف العدد المضروب بـ5 ثم ضربه بـ10 فمثلاً 6×5 هو 30=10×3 (حيث 3 هو نصف العدد 6)، ويمكن ضرب العدد 6بـ10 ليكون ناتج 6×5 هو نصف ناتج 6×10 أي 30.
- في جدول الضرب بالعدد 6، عند ضرب عدد زوجي بـ6 ستكون مرتبة الآحاد في الناتج هي الرقم الزوجي نفسه، كما في 12=2×6 و 24=4×6 و 36=6×6
- لحفظ ناتج 56=7×8 يجب تذكر ترتيب الأرقام 5،6،7،8 (8×7=56).
- قاعدة حفظ جدول العدد 8 هي: ضاعف ضاعف ضاعف أي: 6×8 هي 12=6×2 ثم 24=12×2 ثم 48=24×2.
- لتسهيل الضرب بالعدد 9 توجد عدة طرق:
- نقوم بضرب الرقم بالعدد 10 ثم نطرحه من الناتج كما في 54=6×9 هي نفسها 6-6×10 أي 54=6-60
- آحاد نواتج ضرب الأرقام من 1 إلى 10 بالرقم 9 هي بالترتيب 6،7،8،9،..الخ أي 9=1×9 و18=2×9 و27=3×9 وهكذا، أما عشرات نواتج ضرب الأرقام من 1 إلى 10 بالرقم 9 هي بالترتيب 3،2،1،0،...الخ أي 09=1×9 و 18 =2×9 و27 =3×9 وهكذا.
- طرح واحد من الرقم المضروب يعطي رقم العشرات للناتج ويكون الآحاد هو ناتج طرح 9 من رقم العشرات كما في المثال التالي 45=5×9، حيث رقم العشرات هو ناتج 4=1-5 والآحاد هو ناتج 5=4-9.
- يمكن أيضاً استخدام خدعة اليد التي ذُكرت سابقاً.
- لضرب الأرقام ب10 نضيف صفراً إلى يمين الرقم فقط أي 20 =2×10.
- لضرب رقم ما بـ11 نكتب الرقم في الناتج مرتين أي 99=9×11، أما لضرب الأعداد من 10 إلى 18 بـ11 يكون بوضع ناتج جمع رقمي الآحاد والعشرات للعدد المضروب وتوسيطه بين آحاده وعشراته مثل 165=15×11 حيث الرقم 6 هو ناتج 5+1، وفي حال كان ناتج جمعهما أكبر من 9 نقوم بإضافة الواحد لعشرات العدد المضروب أي لإيجاد ناتج 75×11 نجمع 12=7+5 نضع الرقم 2 بين آحاد وعشرات العدد ( أي بين 5 و7) ونضيف 1 إلى عشراته (أي إلى 7) فيصبح الناتج 825.
- للضرب بـ12 نقسم 12 إلى 10 و2 حيث يُضرب الرقم بـ10 ويُجمع مع ناتج ضربه بـ2 مثل 4×12 يمكن تجزئته إلى 10×4+2×4 أي 48=40+8، ونفس الطريقة تطبق عند الضرب بـ15.
- للضرب بـ20 نضرب الرقم بـ10 ثم نضاعفه كما في 4×20 هي 4*10=40 حيث 40 هي حاصل ضرب 4 بـ10 ثم نضاعف الناتج: 40*2=80.
- إليك أيضًا هذا الفيديو التعليمي لتحفيظ جدول الضرب بسهولة:

حفظ جدول الضرب للاطفال
يُعدّ تعليم جدول الضرب للأطفال من أهمّ المشاكل التي يعاني منها الوالدان قبل الأطفال أنفسهم، وقبل كلّ شيءٍ علينا أن نعلم أن أجمل ما في الرياضيات هو المرونة التي تتمتع بها الأرقام وهو ما يطلق عليه بـ "إحساس الرقم"، لذلك وعلى الرّغم من أهمية الحقائق الرياضية في جدول الضرب إلّا أنّ التركيز على الحفظ التكراري دون التفاعل مع الأرقام يعدّ المثبط الأكبر للمهارات الذهنية الإبداعية عند الطفل، ممّا يحول اهتمام الطفل عن الرياضيات الذي يختلف عن غيره من المواد التي يدرسها الطالب في مدرسته كاللغة الأجنبية.
الطالب الذي يعتمد على ذاكرته فقط في جدول الضرب سيقع في معضلة النسيان التي يعاني منها أيّ دماغٍ طبيعيٍّ، فعلى سبيل المثال قد ينسى الطالب جداء 7×8 ولكن الطالب المتمرّن سيعلم أنها مجرد إضافة سبعة إلى حاصل جداء 7×7 أي 49+7 وهو 56.
ولتعليم أطفالكم حفظ جدول الضرب بطريقةٍ بسيطةٍ وسهلةٍ فهناك عدّة خطواتٍ لا بدّ من اتباعها:
ربط الضرب بعملية الجمع
من بديهيات جدول الضرب هو ربطه بعملية الجمع لمعرفة أساس العملية، وهو إضافةٌ متكرّرةٌ للرقم للحصول على مضاعفات العدد، على سبيل المثال العملية 4 × 3 هي جمع الرقم 4 مع نفسه لثلاث مرّات، أي:
4×3=4 +4 +4 =12
البدء بأسهل الجداول وهو جدول الضرب للعددين(0-1)
الضرب بـ 0
وفقًا لخاصيّة الإضافة فإنّ إضافة العدد صفر لأيّ رقمٍ لا يمثّل أيّ إضافةٍ، كما أنّ ضرب العدد صفر بأيّ رقمٍ يعني تكراره صفر مرّة؛ أي دون تكرار له، وبالتالي ضرب أيّ رقمٍ بالعدد صفر يساوي للصفر، مثال: 5×0= 0
ومن الممكن ربط الخاصية ببعض الأمثلة لتوضيح الفكرة للطفل، فصحنٌ يحوي خمس حبّات تفاحٍ يحوي صفرًا من الموز، أي تكرار أو عدد قرون الموز في صحن التفاح هو صفر.
الضرب بالرقم 1
وهو ما يُطلق عليه بخاصّية الهوية أو التعريف، لأن ناتج ضرب أي رقم بالعدد واحد هو الرقم نفسه، وفقًا لخاصية الإضافة أو الجمع، فالضرب بالعدد واحد يعني تكرار الرقم لمرة واحدة، أي: 2×1=2
ومن الممكن تجسيد الفكرة في مثالٍ واقعيٍّ، كما في عدد أيام الأسبوع في صفٍّ واحدٍ ضمن التقويم وهو سبعة أيام في أسبوعٍ واحد.
تغطية كامل جدول الضرب - قم بإنشاء مخططٍ أو رسمٍ بياني لجدول الضرب 10×10.
- تعليم الطالب حول كيفية تتبع البيانات على الجدول باستخدام المحورين الأفقي والعمودي.
- الآن يمكنك اتباع الحيل السابقة الذكر للعثور على أنماطٍ محددّةٍ في المخطط، كما في جدول الرقم عشرة والذي تنتهي جميع نواتجه بالصفر.
- الآن يمكنك حذف نتائج الجداول السهلة كجدول الرقم واحد والعشرة، والبعض يجد نفس السهولة في حفظ واستنتاج جدول العدد 2 أو 5 ، وباستمرار حذفك للبيانات التي أصبحت واضحةً ومعروفةً لديك ستقلّ كمية البيانات المتبقية لتتعلمها.
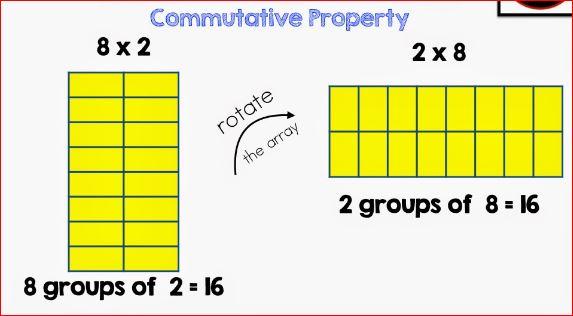
أهميّة خاصية التبديل في تسهيل عملية الضرب
كما الجمع، يُعدّ الضرب عمليةً تبادليةً، وبالتالي لن تختلف قيمة الناتج في حال عكس القيم المتفاعلة، على سبيل المثال:
4×3=3×4=12
4+4+4=3+3+3+3=12
وبالتالي فإن نصف البيانات في المخطط مكررّةً، ممّا يحفّز الأطفال على تعلم ما تبقى من البيانات.
تعلم مضاعفات الأعداد
الخطوة الأخيرة المساعدة هي بتعلم الحصول على مضاعفات كلّ رقمٍ وفقًا لخاصية الإضافة، وبالتالي تكون قد حصلت على مخططٍ كامل البيانات لجدول الضرب من 1 حتى 10.
أفضل الطرق لحفظ جدول الضرب
أصبح طفلك الآن في السادسة من عمره، وهو مستعدٌ للقيام بعملية الضرب الرياضية، بعد تركيز مفهوم الأرقام بشكلٍ تصويريٍّ وتجريديٍّ وملموس في ذهنه، وبعد توضيح أهمية الرياضيات في حياتنا اليومية ومقارنتها بأمثلةٍ واقعيةٍ بشكلٍ دائمٍ.
ولفهم عملية الضرب لا بدّ من فهم محتواها المرتبط بعملية الجمع، وبخصائص العملية التبادلية، ممّا يمكنهم من حفظ جدول الضرب بطرقٍ إستنتاجيةٍ، ليبقى في ذاكرتهم على مدى الحياة، ومن الأساليب الممكن إتباعها لتوضيح عملية الضرب ما يلي:
النمذجة الشريطية
هي عمليةٌ تصويريةٌ للأرقام لتوضيح ما تعنيه، باستخدام أشرطةٍ مقسّمةٍ إلى مستطيلاتٍ، على سبيل المثال إليك العملية الحسابية التالية: 2×3=2+2+2
فالمستطيل الواحد يحمل قيمة الرقم 2، ومنه يمكن تمثيل العملية السابقة بثلاث مستطيلات تحمل قيمة الرقم 2، وبالتالي: 2×3=2+2+2=6

كذلك توضح لنا النمذجة الشريطية مفهوم التبادلية في الضرب، فالنتيجة لا تتغيرلأن:
2×3=3+3=6
2×3=2+2+2=6
وهو ما يختلف كليًّا في عملية القسمة فهي لبست تبادلية، ففي المثال السابق:
6 ÷ 2 = 3
2 ÷ 6 = 0.33333333333
المصفوفات
هي تصويرٌ حيٌّ لجدول الضرب، ممّا يوصل فكرة العملية الحسابية إلى ذهن الطفل بشكلٍ تصويريٍّ، تعتمد على توضيح الأرقام على شكل مجموعاتٍ أو حصصٍ، ففي المثال السابق، 3×2 هي ثلاث مجموعات من ثنائيات، أو يمكن صياغتها بطريقة مختلفة؛ 2×3 هي مجموعتان من ثلاثة نقاط، والنتيجة واحدة، فيمكن تمثيل الرقم 6 في عدة مصفوفات أو مجموعات.

الضرب باستخدام مستقيم الأعداد
تطبيقًا لعملية الجمع خلال الضرب، فإنّ مستقيم الأعداد من أوضح الطرق لإيصال فكرة التخطي أو القفز، فهو القيام بتنقلاتٍ على مستقيم الأعداد بحجم عددٍ، وبعدد المجموعات، فهو تمثيل واضح للانتقال بين المضاعفات بالجمع بالعدد ذاته، على سبيل المثال: 3×4
هو عدد ثلاث مجموعات من أربعة كائنات، فبعد رسم مستقيم الأعداد نبدأ من النقطة صفر للانطلاق في ثلاث قفزات، وكلّ قفزةٍ بالحجم 4، كما يلي:

وبذلك نصل إلى النتيجة المطلوبة 12 بالانتقال بين مضاعفات العدد 4: 4-8-12، بإضافة 4 في كل قفزة.
في مثال آخر، لحساب 5×2 علينا بالقفز خمس مرات وكل قفزة بحجم الرقم 2، وبذلك ننتقل بين مضاعفات العدد 2 بإضافة 2 في كل قفزة حتى نصل إلى النتيجة الصحيحة: 2_4_6_8_10.

وبذلك نصل إلى الرقم 10.
تمارين جدول الضرب
أفضل وسيلةٍ لإيصال مفهوم جدول الضرب للطفل هي بمعرفة أهميته والغاية منه، عبر بعض الأمثلة الحياتية اليومية، وإليك بعض التمارين الواقعية:
كم عدد البيض لدجاجة تبيض بيضتان في كلَ يوم على مدى ثلاثة أيام؟
هنا يمكن حساب عدد البيض المقسّم على ثلاث مجموعاتٍ وهي الأيام الثلاثة، بضرب عدد البيضات في اليوم الواحد بعدد الأيام:

- كم العدد الإجمالي للكعكات الموجودة في حقيبتين مملوءتين بخمس كعكاتٍ؟
- تحتوي الحقيبة الوحدة على خمس كعكات وبالتالي العدد الكلي هو ناتج ضرب عدد الكعكات بالحقيبة الواحدة بعدد الحقائب: 5×2=5+5= 10
- ما ثمن شرائك لأربعة حقائب كلٍّ منها بسعر 6 بنسات؟
- ستدفع 6 بنسات لكلّ حقيبةٍ من الحقائب الربعة فالثمن هو ناتج جمع 6 لأربع مرات، أي الوصول لمضاعفات الرقم 6 أربع مرات: 6×4 =6+6+6+6= 24
- ما تكلفة شرائك لثلاث علب جبنة بسعر 10 جنيه للواحدة؟
- عليك أن تدفع 10 جنيه ثلاث مرات لعلب الجبنة الثلاث، أي: 10×3= 10+10+10= 30
جدول الضرب كامل بالعربي من 1 إلى 12
جدول ضرب 1 - 1×1=1
- 2×1=2
- 3×1=3
- 4×1=4
- 5×1=5
- 6×1=6
- 7×1=7
- 8×1=8
- 9×1=9
- 10×1=10
- 11×1=11
- 12×1=12
- جدول ضرب العدد 2
- 2 ×1 = 2
- 2 × 2= 4
- 2 × 3= 6
- 2 × 4= 8
- 2 × 5= 10
- 2 × 6= 12
- 2 × 7= 14
- 2 × 8= 16
- 2 × 9= 18
- 2×10=20
- 2 × 11= 22
- 2 × 12= 24
- جدول ضرب العدد 3
- 3 × 1= 3
- 3 × 2= 6
- 3 × 3= 9
- 3 × 4= 12
- 3 × 5= 15
- 3 × 6= 18
- 3 × 7= 21
- 3 × 8= 24
- 3 ×9 = 27
- 3 ×10 = 30
- 3 ×11 = 33
- 3 ×12 = 36
- جدول ضرب العدد 4
- 4 × 1= 4
- 4 × 2= 8
- 4 × 3= 12
- 4 × 4= 16
- 4 × 5= 20
- 4 × 6= 24
- 4 × 7= 28
- 4 × 8= 32
- 4 × 9= 36
- 4 × 10= 40
- 4 × 11= 44
- 4 × 12= 48
- جدول ضرب العدد 5
- 5 × 1= 5
- 5 × 2= 10
- 5 × 3= 15
- 5 × 4= 20
- 5 × 5= 25
- 5 × 6 = 30
- 5 × 7= 35
- 5 × 8 =40
- 5 × 9 = 45
- 5 × 10= 50
- 5 × 11= 55
- 5 × 12= 60
- جدول ضرب العدد 6
- 6 × 1= 6
- 6 × 2= 12
- 6 × 3= 18
- 6 × 4= 24
- 6 × 6= 36
- 6 × 5= 30
- 6 × 6= 36
- 6 × 7= 42
- 6 × 8 = 48
- 6 × 9 = 54
- 6 × 10 = 60
- 6 × 11 = 66
- 6 × 12 = 72
- جدول ضرب العدد 7
- 7 × 1 = 7
- 7 × 2 = 14
- 7 × 3 = 21
- 7 × 4 = 28
- 7 × 5 = 35
- 7 × 6 = 42
- 7 × 7 = 49
- 7 × 8 = 56
- 7 × 9 = 63
- 7 × 10 = 70
- 7 × 11 = 77
- 7 × 12 = 84
- جدول ضرب العدد 8
- 8 × 1 = 8
- 8 × 2 = 16
- 8 × 3 = 24
- 8 × 4 = 32
- 8 × 5 = 40
- 8 × 6 = 48
- 8 × 7= 56
- 8 × 8 = 64
- 8 × 9 = 72
- 8 × 10 = 80
- 8 × 11 = 88
- 8 × 12 = 96
- جدول ضرب العدد 9
- 9 × 1 = 9
- 9 × 2 = 18
- 9 × 3 = 27
- 9 × 4 = 36
- 9 × 5 = 45
- 9 × 6 = 54
- 9 × 7 = 63
- 9 × 8 = 72
- 9 × 9 = 81
- 9 × 10 = 90
- 9 × 11 = 99
- 9 × 12 = 108
- جدول ضرب العدد 10
- 10 × 1 = 10
- 10 × 2 = 20
- 10 × 3 = 30
- 10 × 4 = 40
- 10 × 5 = 50
- 10 × 6 = 60
- 10 × 7 = 70
- 10 × 8 = 80
- 10 × 9 = 90
- 10 × 10 = 100
- 10 × 11= 110
- 10 × 12 = 120
- جدول ضرب 11
- 11 × 1 = 11
- 11 × 2 = 22
- 11 × 3 = 33
- 11 × 4 = 44
- 11 × 5 = 55
- 11 × 6 = 66
- 11 × 7 = 77
- 11 × 8 = 88
- 11 × 9 = 99
- 11 × 10 = 110
- 11 × 11 = 121
- 11 × 12 = 132
- جدول ضرب 12
- 12 × 1 = 12
- 12 × 2 = 24
- 12 × 3 = 36
- 12 × 4 = 48
- 12 × 5 = 60
- 12 × 6 = 72
- 12 × 7 = 84
- 12 × 8 = 96
- 12 × 9 = 108
- 12 × 10 = 120
- 12 × 11 = 132
- 12 × 12 = 144
