متتالية فيبوناتشي
متتالية فيبوناتشي أو أعداد فيبوناتشي في الرياضيات هي الأرقام التي تكون في المتتالية التالية:
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , … . {\displaystyle 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89 ,\;144,\;\ldots .}
بتعريفها فإن أول من أرقام فيبوناتشي هما 0 و 1، ويكون كل رقم هو نتاج مجموع الرقمين السابقين له. بعض المدارس حذفت الرقم 0 الأساسي واستبدلته بالرقم 1 مرتين.
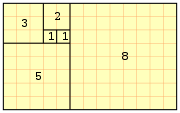
تبليط المربعات بحيث يكون الجانبين هما ارقام فيبوناشي المتتالية في الطول

يوبانا (en) (وتعني بالكيشوا أداة عد) وهي آلة حسابية استخدمها الإنكا. يعتقد الباحثون بأن تلك الحسابات اعتمدت على أرقام فيبوناشي لتقليل عدد الحبوب اللازمة لكل حقل[1].

لولب فيبوناتشي بطريقة رسم أقواس متصلة بالزوايا المتقابلة من المربعات في تبليط فيبوناتشي، ويستخدم لأحجام المربعات التالية 1، 1، 2، 3، 5، 8، 13، 21، 34، انظر الدوامة الذهبية (en)
تعرف المتتالية Fn لرقم فيبوناتشي بالوصف الرياضياتي بالعلاقة المتكررة (en)
F n = F n − 1 + F n − 2 , {\displaystyle F_{n}=F_{n-1}+F_{n-2},\!\,}
مع القيم الناتجة منها
F 0 = 0 and F 1 = 1. {\displaystyle F_{0}=0\quad {\text{and}}\quad F_{1}=1.}
سميت متتالية فيبوناتشي نسبة إلى ليوناردو البيسي والمعروف باسم فيبوناتشي (باللاتينية: Fibonacci) وتعني ابن بوناشيو filius Bonaccio. وكتابه الذي ألفه سنة 1202 واسمه ليبري أباتشي (en) حيث عرف المتتالية في رياضيات الغرب الأوروبي، وقد كانت تلك المتتالية معروفة وموصوفة بالسابق في الرياضيات الهندية[2][3].
استخدمت أرقام فيبوناتشي في تحليل الأسواق المالية، في استراتيجيات مثل ارتداد فيبوناتشي وفي خوارزميات االكمبيوتر مثل تقنية فيبوناتشي للبحث (en) وهيكلة بيانات تكدس فيبوناتشي (en). وهي تظهر أيضا في الترتيبات البيولوجية[4]، مثل تفريعات الأشجار، ترتيب الأوراق على الساق (en) وطرف الثمرة من الأناناس[5] وتفتح الخرشوف والسرخس غير المتجعد وترتيب مخروط الصنوبر
متتالية فيبوناتشي أو أعداد فيبوناتشي في الرياضيات هي الأرقام التي تكون في المتتالية التالية:
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , … . {\displaystyle 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89 ,\;144,\;\ldots .}

بتعريفها فإن أول من أرقام فيبوناتشي هما 0 و 1، ويكون كل رقم هو نتاج مجموع الرقمين السابقين له. بعض المدارس حذفت الرقم 0 الأساسي واستبدلته بالرقم 1 مرتين.

تبليط المربعات بحيث يكون الجانبين هما ارقام فيبوناشي المتتالية في الطول
 مقالة مفصلة: النسبة الذهبية
مقالة مفصلة: النسبة الذهبية

يوبانا (en) (وتعني بالكيشوا أداة عد) وهي آلة حسابية استخدمها الإنكا. يعتقد الباحثون بأن تلك الحسابات اعتمدت على أرقام فيبوناشي لتقليل عدد الحبوب اللازمة لكل حقل[1].

لولب فيبوناتشي بطريقة رسم أقواس متصلة بالزوايا المتقابلة من المربعات في تبليط فيبوناتشي، ويستخدم لأحجام المربعات التالية 1، 1، 2، 3، 5، 8، 13، 21، 34، انظر الدوامة الذهبية (en)
تعرف المتتالية Fn لرقم فيبوناتشي بالوصف الرياضياتي بالعلاقة المتكررة (en)
F n = F n − 1 + F n − 2 , {\displaystyle F_{n}=F_{n-1}+F_{n-2},\!\,}

مع القيم الناتجة منها
F 0 = 0 and F 1 = 1. {\displaystyle F_{0}=0\quad {\text{and}}\quad F_{1}=1.}

سميت متتالية فيبوناتشي نسبة إلى ليوناردو البيسي والمعروف باسم فيبوناتشي (باللاتينية: Fibonacci) وتعني ابن بوناشيو filius Bonaccio. وكتابه الذي ألفه سنة 1202 واسمه ليبري أباتشي (en) حيث عرف المتتالية في رياضيات الغرب الأوروبي، وقد كانت تلك المتتالية معروفة وموصوفة بالسابق في الرياضيات الهندية[2][3].
استخدمت أرقام فيبوناتشي في تحليل الأسواق المالية، في استراتيجيات مثل ارتداد فيبوناتشي وفي خوارزميات االكمبيوتر مثل تقنية فيبوناتشي للبحث (en) وهيكلة بيانات تكدس فيبوناتشي (en). وهي تظهر أيضا في الترتيبات البيولوجية[4]، مثل تفريعات الأشجار، ترتيب الأوراق على الساق (en) وطرف الثمرة من الأناناس[5] وتفتح الخرشوف والسرخس غير المتجعد وترتيب مخروط الصنوبر
