قانون ذي الحدين
قانون ذي الحدين binomial law، هو القانون الذي يعطي مفكوك القوة n لمجموع عددين a وb؛ حيث ينتمي n لمجموعة الأعداد الطبيعية N، (أي مفكوك (a + b)2 حيث n ∈ N).
أول من درَس هذا الموضوع (حسب الوثائق المعروفة حالياً) هو العالم العربي أبو بكر محمد بن الحسين الكرجي (أو الكرخي) في القرن الحادي عشر الميلادي. وقد ذكر مفكوك القوة الثانية والثالثة والرابعة والخامسة، وعرف أن عدد حدود المفكوك للقوة n هو n +1. وأن الحدود هي من الشكل λi an - i bi حيث λi هي أمثال الحد i؛ i = 0, …, n. أي أن
ثم أورد قاعدة لمعرفة أمثال المفكوك من أي مرتبة، كما ذكر السموءل بن يحيى بن عباس المغربي (توفي نحو سنة 570هـ/1175م) في كتابه «الباهر»:
«قال الكرجي: إذا أردت ذلك وضعت على التخت واحدًا وواحداً تحته، ثم نقلت الواحد إلى سطر آخر وضممت الواحد إلى الواحد الذي تحته يكون اثنين ووضعته تحته، ثم وضعت الواحد الآخر تحته فيصير واحداً واثنين وواحداً، ثم نقلنا الواحد من السطر الثاني إلى سطر آخر، وضممت الواحد إلى الاثنين يكون ثلاثة كتبناها تحت الواحد، وضممنا الاثنين إلى الواحد الذي تحتها فتصير ثلاثة، ثم وضعت الواحد الآخر تحته فيصير واحداً وثلاثة وثلاثة وواحداً» وهكذا. كما في الجدول التالي (المأخوذ من مخطوطة كتاب «الباهر»):
الذي يعطي أمثال مفكوك ذي الحدين حتى المرتبة الثانية عشرة، مثلاً:
a + b)7 =a7 + 7a6 b +21a5 b2 + 35a4 b3 + 35a3 b4 + 21a2 b5 + 7a b6 + b7)
وبرهان ذلك سهل باعتماد مبدأ الاستقراء الرياضي[ر]:
1) إن القضية محققة من أجل n = 2 إذ إن:
a + b)2 =(a + b) + (a + b) = a2 + 2ab + b2)
2) نفرض أن القضية صحيحة من أجل n = k، ولنبرهن على صحتها من أجل n = k + 1
(a + b)k+1 =(a + b)k + (a + b)
(ak + a1ak-1b +...+ a1ak-1b +...+ ak-1abk-1+ bk) (a + b) =
ak+1 + b1akb +...+ b1ak+1- i bi +...+ bkabk + bk+1 =
حيث b0=bk+1و bi=ai+ai-1حيث i = 1, …, k
ومن ثم فالقضية صحيحة دوماً، مهما تكن المرتبة n.
وبذا كان السبق للعالم العربي أبي بكر الكرجي في اكتشاف قانون ذي الحدين، واكتشاف الطريقة العملية لتحديد الأمثال من مثلث حدد خوارزمية تشكيله.
وجاء بعد ذلك العالم البريطاني إسحاق نيوتن [ر] (1642-1727) I.Newton، وكتب القانون بالشكل:
فعرف باسم «قانون نيوتن» أو «قانون ذي الحدين» والبعض يدعوه «قانون الكرجي ـ نيوتن».
والأحق أن يدعى «قانون الكرجي» نسبة إلى أول من وضعه.
واستفاد العالم الفرنسي بليز باسكال[ر] (1623ـ1662) Blaise Pascal من ملاحظة أن
فأعاد تشكيل مثلث الأمثال معتمدًا الخوارزمية نفسها التي كتبها الكرجي، فعرف هذا المثلث باسمه «مثلث باسكال».
والأحق أن يدعى «مثلث الكرجي» نسبة إلى أول من وضعه.
مثال (1): بفرض a = 1 و b = x يكون:
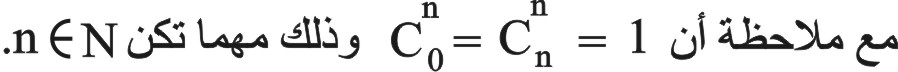
فمثلاً عندما n = 10:
مثال (2): بفرض a = 1 و b = 1 يكون:
أنور توفيق اللحام
قانون ذي الحدين binomial law، هو القانون الذي يعطي مفكوك القوة n لمجموع عددين a وb؛ حيث ينتمي n لمجموعة الأعداد الطبيعية N، (أي مفكوك (a + b)2 حيث n ∈ N).
أول من درَس هذا الموضوع (حسب الوثائق المعروفة حالياً) هو العالم العربي أبو بكر محمد بن الحسين الكرجي (أو الكرخي) في القرن الحادي عشر الميلادي. وقد ذكر مفكوك القوة الثانية والثالثة والرابعة والخامسة، وعرف أن عدد حدود المفكوك للقوة n هو n +1. وأن الحدود هي من الشكل λi an - i bi حيث λi هي أمثال الحد i؛ i = 0, …, n. أي أن
 |
«قال الكرجي: إذا أردت ذلك وضعت على التخت واحدًا وواحداً تحته، ثم نقلت الواحد إلى سطر آخر وضممت الواحد إلى الواحد الذي تحته يكون اثنين ووضعته تحته، ثم وضعت الواحد الآخر تحته فيصير واحداً واثنين وواحداً، ثم نقلنا الواحد من السطر الثاني إلى سطر آخر، وضممت الواحد إلى الاثنين يكون ثلاثة كتبناها تحت الواحد، وضممنا الاثنين إلى الواحد الذي تحتها فتصير ثلاثة، ثم وضعت الواحد الآخر تحته فيصير واحداً وثلاثة وثلاثة وواحداً» وهكذا. كما في الجدول التالي (المأخوذ من مخطوطة كتاب «الباهر»):
 |
a + b)7 =a7 + 7a6 b +21a5 b2 + 35a4 b3 + 35a3 b4 + 21a2 b5 + 7a b6 + b7)
وبرهان ذلك سهل باعتماد مبدأ الاستقراء الرياضي[ر]:
1) إن القضية محققة من أجل n = 2 إذ إن:
a + b)2 =(a + b) + (a + b) = a2 + 2ab + b2)
2) نفرض أن القضية صحيحة من أجل n = k، ولنبرهن على صحتها من أجل n = k + 1
 |
(ak + a1ak-1b +...+ a1ak-1b +...+ ak-1abk-1+ bk) (a + b) =
ak+1 + b1akb +...+ b1ak+1- i bi +...+ bkabk + bk+1 =
حيث b0=bk+1و bi=ai+ai-1حيث i = 1, …, k
ومن ثم فالقضية صحيحة دوماً، مهما تكن المرتبة n.
وبذا كان السبق للعالم العربي أبي بكر الكرجي في اكتشاف قانون ذي الحدين، واكتشاف الطريقة العملية لتحديد الأمثال من مثلث حدد خوارزمية تشكيله.
وجاء بعد ذلك العالم البريطاني إسحاق نيوتن [ر] (1642-1727) I.Newton، وكتب القانون بالشكل:
 |
 |
والأحق أن يدعى «قانون الكرجي» نسبة إلى أول من وضعه.
واستفاد العالم الفرنسي بليز باسكال[ر] (1623ـ1662) Blaise Pascal من ملاحظة أن
 |
والأحق أن يدعى «مثلث الكرجي» نسبة إلى أول من وضعه.
مثال (1): بفرض a = 1 و b = x يكون:
 |
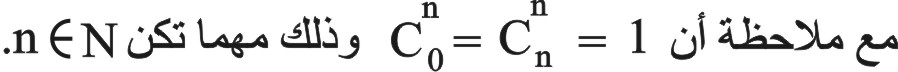
فمثلاً عندما n = 10:
 |
 |
 |
