تويت
الفضاء الإقليدي الثلاثي البعد
وضع العالم الرياضي اليوناني إقليدس (330-275ق.م) حجر الأساس لعلم الهندسة، حيث حدد خمس فرضيات postulates, axioms (مصادرات)، احتلت مركزاً ممتازاً في تاريخ الرياضيات، باعتمادها أساساً لعلم الهندسة حيناً من الدهر جاوز العشرين قرناً. وحتى اليوم، فإن الهندسة التي تدرَّس أساساً في المدارس والجامعات هي «هندسة إقليدس». كما وأن كتاب إقليدس «الأصول»، والذي يتألف من ثلاثة عشر جزءاً، لا يزال يطبع حتى اليوم مترجماً إلى أكثر لغات العالم.
وقد أورد إقليدس فرضياته الخمس المشهورة في كتابه «الأصول» على النحو الآتي:
1 - يمكن رسم مستقيم مار بأي نقطتين.
2 - يمكن تمديد القطعة المستقيمة بلا حدود حتى تصبح مستقيماً.
3 - يمكن رسم دائرة مركزها ونصف قطرها اختياريان.
4 - كل الزوايا القائمة متساوية فيما بينها.
5 - إذا قطع مستقيم مستقيمين آخرين واقعين في مستو واحد، وكان مجموع قياسي الزاويتين الداخليتين في إحدى جهتي المستقيم القاطع أصغر من مجموع قياسي زاويتين قائمتين، فإن المستقيمين الآخرين يتقاطعان في هذه الجهة.
ولما كانت الفكرة السائدة بين الرياضيين هي أن صحة الفرضية تقاس بوضوحها، فقد قبلوا الفرضيات الأربع من دون نقاش، أما الفرضية الخامسة فلم تكن واضحة لديهم، إذ أنها أعقد بكثير من الفرضيات السابقة لها، لذا ساد الاعتقاد بين الرياضيين بأن ما أسماه إقليدس فرضية خامسة، إن هي إلا مبرهنة (نظرية) تستند إلى ما قبلها من الفرضيات، وقد ظل الرياضيون في مشارق الأرض ومغاربها يجرون المحاولة تلو الأخرى للبرهان على فرضية إقليدس الخامسة قرابة ألفي سنة؛ بيد أن محاولاتهم كلها ذهبت أدراج الرياح. وقد اعتقد كثير منهم بأنهم قد أفلحوا في البرهان على هذه الفرضية ؛ إلا أنه عند التعمق في دراسة هذه البراهين، وجد أنها تحوي إما غلطة منطقية، أو فرضية أخرى مكافئة للفرضية قيد البرهان.
والفرضية المكافئة للفرضية الخامسة، والتي يحفظها الجميع هي:
«لا يمكن أن نرسم غير مستقيم واحد مواز لمستقيم مفروض من نقطة خارجة عنه». إن هذا الغموض الذي اكتنف الفرضية الخامسة في مدة تزيد على العشرين قرناً أدى إلى أن بعض العلماء أخذوا من إقليدس فرضياته الأربع الأولى، وأضافوا إليها فرضية خامسة تعاكس فرضيته الخامسة، فاكتشفوا عدم وجود تناقض بين مجموعة فرضياتهم الخمس الجديدة، مما قاد إلى:
1 - إثبات حقيقة استقلال فرضية إقليدس الخامسة عن فرضياته الأربع الأولى.
2 - اكتشاف هندسات جديدة «لا إقليدية» سميت بأسماء مكتشفيها.
من هذه الهندسات اللاإقليدية هندسة لاباتشيفسكي Lobachevisky ما بين (1792-1856) وهندسة ريمان Riemann.
الفضاء (الهندسي) الإقليدي Euclidean (geometrical) space
هو مجموعة نقاط الفضاء الهندسي العادي، أي الذي يخضع لفرضيات إقليدس.
الفضاء الإقليدي ثلاثي البعد Three Dimensional Euclidean Space
لتكن O نقطة محددة، OX, OY, OZ ثلاثة محاور متعامدة ثابتة، في الفضاء الإقليدي الهندسي، ولتكن الأشعة الثلاثة
هي أشعة القاعدة على المحاور OX, OY, OZ فهي متعامدة مثنى مثنى وتشكل ثلاثية مباشرة. إن الجملة OXYZ تسمى جملة إحداثية متعامدة منظمة (الشكل-1).
إن الفرضية الخامسة لإقليدس - والتي تم ذكر فرضية مكافئة لها: «لا يمكن إنشاء سوى مستقيم واحد L يوازي مستقيماً مفروضاً D من نقطة ما M خارجة عنه» - تجعل بالإمكان تعيين أي نقطة في الفضاء بإحداثياتها نسبة إلى جملة إحداثية مؤلفة من ثلاثة محاور ثابتة.
أي أن كل نقطة M من الفضاء R3 تتعين بثلاثة أعداد حقيقية x, y, z. أي يقابلها ثلاثية وحيدة (x, y, z)، حيث x, y, z هي مركبات المتجه OM على المحاور OX, OY, OZ - والعكس بالعكس (الشكل-2).
أي إنه يوجد تقابل بين نقاط الفراغ الهندسي الإقليدي المنسوب إلى جملة محاور إحداثية OXYZ وبين مجموعة الجداء الديكارتي R3 = {(x, y, z)}: x, y, z ∈ R} حيث R هي مجموعة الأعداد الحقيقية. إن هذا يجعل كل منحن أو سطح أو مجسم في R3 يمثل بعدد من المعادلات، تساعد على دراسته ومعرفة خواصه، وهذا هو مجال الهندسة التحليلية.
مثال : معادلة كرة مركزها M0 (x0, y0, z0) ونصف قطرها a هو :
(x - x0)2 +(y - y0)2 + (z - z0)2 = a2
تعريف: الفضاء الإقليدي هو فضاء حقيقي مزود بجداء داخلي.
الفضاء الحقيقي هو فضاء متجهي[ر] معرف على حقل الأعداد الحقيقية R.
الجداء الداخلي على فضاء حقيقي E هو تطبيق *: E . E → R; (u, v) → u*v يحقق الشروط الآتية:
1) (u + v) * v = u* v + w * v ∀ u, w, v ∈ E
2) v * (u + w) = v * u + v * w ∀ u, w, v ∈ E
3) (a.u) * v = a (u * v) ∀ a ∈ E; ∀ u, v ∈ E
4) (u * v) = v * u ∀ u, v ∈ E
5) u * u ≥ 0 ∀ u ∈ E
6) u = 0 ⇔ u * u = 0
الفضاء المتجهي الحقيقي (real vector space) R3
يعرف على المجموعة R3 = {(x, y, z)}: x, y, z ∈ R} عمليتي جمع، وضرب بعدد كما يأتي:
ـ حاصل جمع متجهين a (a1, a2, a3) وb (b1, b2, b3) من R3 هو متجه ثالث c = (c1, c2, c3) = (a1 + b1, a2 + b2, a3 + b3)
ـ حاصل ضرب متجه a (a1, a2, a3) من R3 بعدد حقيقي λ من R هو متجه d يوازي المتجه a ويساوي d = (.λ .a1, .λ .a2, .λ .a3).
ـ إن المجموعة R3 = {(x, y, z) : x, y, z ∈ R} مع عمليتي الجمع والضرب بعدد من R، تشكل فضاءً متجهياً حقيقياً.
الجداء الداخلي (العددي، السلمي) inner (scalar) product على R3
إذا كان a (a1, a2, a3) وb (b1, b2, b3) متجهين في فضاء متجهي حقيقيR3 فإن جداء المتجهين a (a1, a2, a3) وb (b1, b2, b3) المعرف بالشكل
a.b = (a1b1 + a2b2 + a3b3) هو جداء داخلي علىR3 .
الفضاء (المتجهي) الإقليدي Euclidean (vector) space R3
إن الفضاء المتجهي الحقيقي R3 مع عملية الجداء الداخلي السابقة، هو فضاء إقليدي.
مثال: الجداء العددي للمتجهين a (- 2, 5, 3), b (3, - 2, 1) هو
a.b = (- 2) (3) +(5) (- 2) + (3) (1) = - 13
طول متجه a (a1, a2, a3)
إن: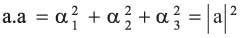
(حيث |a| طول المتجه a)
أي إن طول المتجه a (a1, a2, a3) هو:
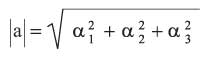
البعد بين نقطتين
إذا كانت M1 (x1, y1, z1) وM2 (x2, y2, z2) نقطتين من الفضاء الإقليدي R3 فإن المتجه M1 M2 = OM2 - OM1 أي أن M1 M2 (x2- x1, y2- y1,z2- z1 وطول هذا المتجه هو:
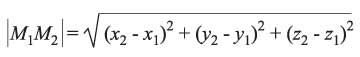
وهو البعد بين النقطتين M1 وM2 (الشكل-3).
مثال: البعد بين النقطتين M1 (-2,3,1) M2 (1,3,-3) هو:
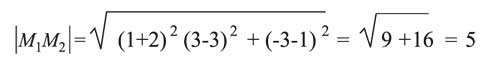
الزاوية بين متجهين
إذا كان المتجهان a (a1, a2, a3) وb (b1, b2, b3) في الفضاء الإقليدي R3 وكانت بينهما زاوية قياسها θ حيث R00 ≤ θ ≤ 1800m ، فيبرهن أن الجداء الداخلي للمتجهين a وb هو:a.b = |a|.|b|.cos θ ومن ثمَّ |cos θ = a.b / |a|.|b
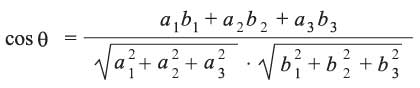
أي θ = arccos (a.b / |a|.|b|) (الشكل-4).
إن |b|.cos θ هو المسقط القائم للمتجه b على المتجه a
كذلك |a|.cos θ هو المسقط القائم للمتجه a على المتجه b
فالجداء الداخلي لمتجهين يساوي طول أحدهما مضروب بالمسقط القائم للمتجه الثاني عليه. ومن ثمَّ فإن مركبات متجه ما a على المحاور الإحداثية OX, OY, OZ هي i.a, j.a, k.a
مثال: لتكن النقاط A (1, 1, 1), B (3, 2, 3), C (0, -1, 1) فلحساب زاوية الرأس C في المثلث ABC، ولتكن θ، تحسب الزاوية بين المتجهين CA, CB
وبفرض a = CA , b = CB يكون a = OA - OC , b = OB - OC
a = (1,1,1) - (0,-1,1) = (1,2,0) وb = (3,2,3) - (0,-1,1) = (3,3,2)
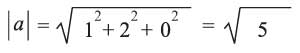و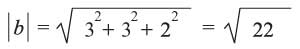
a.b = (1) (3) +(2) (3) +(0) (2) = 9
وتكون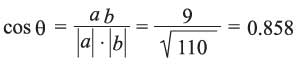
ومن ثمَّ فإن b = 30.9º = 30º 54′
تعامد متجهين
إذا كان المتجهان a ≠ o ≠ b فإن a وb متعامدان إذا كانت الزاوية θ بينهما قائمة، أي إذا كانت cos θ = 0، أي إذا كان الجداء الداخلي للمتجهين يساوي الصفر، أي a.b = 0، أي a1b1 + a2b2 + a3b3 = 0. إذا كان أحد المتجهين a أوb صفراً فإن a.b = 0.
مثال: إن أشعة القاعدة i = (1,0,0), j = (0,1,0), k = (0,0,1) في الفضاء الإقليدي R3 متعامدة مثنى مثنى، حيث إن i . j = j . k = k . j = 0وإن أي متجه
a (a1, a2, a3) من R3 يكتب منسوباً إلى أشعة القاعدة i, j, k بالشكل:
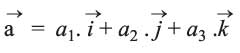
معادلة مستوي في الفضاء الإقليدي
إن معادلة المستوي P المار بالنقطة M1 (x1, y1, z1) والعمودي على المتجه n (a, b, c) هي M1M.n = 0.
حيث M (x, y, z) نقطة ما من المستوي P (الشكل-5)،
أي a (x- x1) + b (y- y1) + c (z- z1) = 0 أي a x + b y + cz = d.
مثال: إن معادلة المستوي المار بالنقطة M1(-2,1,-3) والعمودي على المتجه AB حيث A (2,0,-3), B (-3, -2, 2) هي:
M(-3-2)(x +2) + (-2-0) (y-1) + (2 +3) (z+3) = 0M
M5x + 2y - 5z = 7M
الجداء المتجهي (الخارجي) vector product
الجداء المتجهي لمتجهين a (a1, a2, a3) وb (b1, b2, b3) في فضاء إقليدي R3 هو متجه
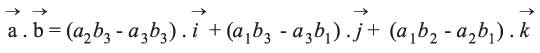
يمكن كتابته بالشكل:
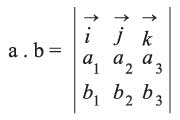
الخواص الجبرية للجداء المتجهي
1) a . b = - b . a (الجداء المتجهي غير تبديلي).
2) a . (b + c) = a . b + a . c (الخاصة التوزيعية) .
3) (.(α . a) (β . b) = (α . β) (a . b وذلك أياً تكن α, β ε R
4) a , b = O إذا كان a وb متوازيين.
5) a . (λ a) = O وذلك أياً يكن a ε R3 وλ ε R.
الجداء المتجهي للأشعة i, j, k
1) i . j = k, j . k = i, k . i = j
2) j . i = - k, k . j = - i, i . k = - j
خواص المتجه P = a . b
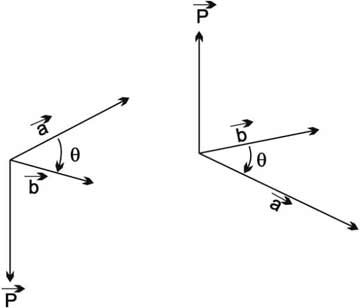
1) المتجه P عمودي على كل من المتجهين a وb، واتجاهه يجعل من الثلاثية [a, b, P] ثلاثية مباشرة (الشكل-6).
2) طول المتجه P يعطى بالعلاقة |P| = |a| . |b| . sin θ حيث θ هي الزاوية بين المتجهين a وb؛n00 ≤ θ ≤ 1800m .
3) المتجه P لا يتغير بتغير الجملة الإحداثية OXYZ.
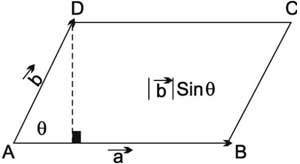
4) مساحة متوازي الأضلاع ABCD تساوي طول الجداء الخارجي للمتجهين AB وAD (أو أي ضلعين آخرين مشتركين برأس واحد) (الشكل-7).
مثال: النقاط الثلاث A (-2,3,-1), B (2,0,-5), C (-3,-1,3) هي رؤوس مثلث ABC
لحساب مساحته يحسب الجداء الخارجي للمتجهين AB وAC
AB = (2 + 2) i + (0 - 3) j + (- 5 + 1) k = 4 i - 3 j - 4 k
AC = (- 3 + 2) i + (- 1 - 3) j + (3 + 1) k = - i - 4 j + 4 k
AB . AC = (- 12 - 16) i - (16 - 4) j + (- 16 - 3) k = - 28 i - 12 j - 19 k
إن مساحة المثلث ABC تساوي
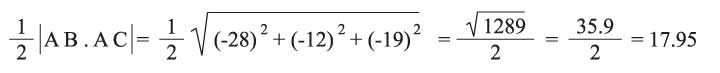
مطابقة لاغرانج
إن العلاقتين |a . b| = |a| . |b| . sin θ
و a . b = |a| . |b| . cos θ
تعطيان (a . b)2 + (|a . b|)2 = |a|2 . |b|2 أي:
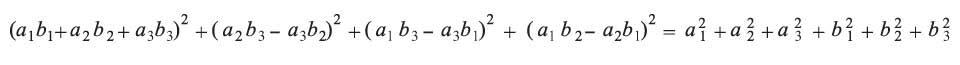
وهي ما تسمى مطابقة لاغرانج.
الجداء المختلط mixed product أو the scalar triple product
إذا كانت الأشعة الثلاث a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3) من الفضاء الإقليدي R3 فإن الجداء العددي a.(b . c) يدعى الجداء المختلط ويرمز له
(a, b, c).
خواص الجداء المختلط للأشعة a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3)
1)
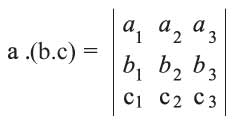
2) a . (b . c) = b . (c . a) = c . (a . b)
3) a . (c . b) = b . (a . c) = c . (b . a) = - a . (b . c)
4) إذا توازى متجهان ( أو تساويا ) فالجداء المختلط a . (b . c) = 0
5) إذا كانت الأحرف الجانبية لمتوازي سطوح ABCDA ′B ′C ′D المنطلقة من أحد الرؤوس تساير (توازي وتساوي) الأشعة a, b, c فإن القيمة المطلقة للجداء المختلط a . (b . c) تساوي حجم متوازي السطوح ABCDA ′B ′C ′D (الشكل-8).
6) إذا كانت الأشعة الثلاث a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3) واقعة في مستوٍ واحد (أو توازي مستوياً واحداً) فإن a . (b . c) = 0
معادلة مستوي يمر من ثلاث نقاط غير واقعة على استقامة واحدة
لتكن M1 (x1, y1, z1) وM2 (x2, y2, z2) وM3 (x3, y3, z3) ثلاث نقاط غير واقعة على استقامة واحدة، ولتكن M (x, y, z) نقطة ما من المستوي M1, M2, M3 فإن الأشعة M1M, M1M2, M1M3 تقع في مستو واحد، ومن ثمَّ فالجداء المختلط لها يساوي الصفر، أي
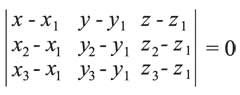
وهي معادلة المستوي الذي يمر من ثلاث نقاط غير واقعة على استقامة واحدة.
مثال: لإيجاد معادلة المستوي المار بالنقاط الثلاث A (-2,3,.-1), B (2,0,-5), C (-3,-1,3)
تؤخذ نقطة ما M (x, y, z) من هذا المستوي ثم تكتب المعادلة
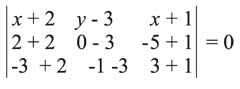
ينتج من نشر المحدد: n(-12 - 16) (x + 2) - (16 - 4) (y - 3) + (-16 -3) (z + 1) = 0
أي إن معادلة المستوي هي:
v28x + 12y + 19z = -39
أنور توفيق اللحام
وضع العالم الرياضي اليوناني إقليدس (330-275ق.م) حجر الأساس لعلم الهندسة، حيث حدد خمس فرضيات postulates, axioms (مصادرات)، احتلت مركزاً ممتازاً في تاريخ الرياضيات، باعتمادها أساساً لعلم الهندسة حيناً من الدهر جاوز العشرين قرناً. وحتى اليوم، فإن الهندسة التي تدرَّس أساساً في المدارس والجامعات هي «هندسة إقليدس». كما وأن كتاب إقليدس «الأصول»، والذي يتألف من ثلاثة عشر جزءاً، لا يزال يطبع حتى اليوم مترجماً إلى أكثر لغات العالم.
وقد أورد إقليدس فرضياته الخمس المشهورة في كتابه «الأصول» على النحو الآتي:
1 - يمكن رسم مستقيم مار بأي نقطتين.
2 - يمكن تمديد القطعة المستقيمة بلا حدود حتى تصبح مستقيماً.
3 - يمكن رسم دائرة مركزها ونصف قطرها اختياريان.
4 - كل الزوايا القائمة متساوية فيما بينها.
5 - إذا قطع مستقيم مستقيمين آخرين واقعين في مستو واحد، وكان مجموع قياسي الزاويتين الداخليتين في إحدى جهتي المستقيم القاطع أصغر من مجموع قياسي زاويتين قائمتين، فإن المستقيمين الآخرين يتقاطعان في هذه الجهة.
ولما كانت الفكرة السائدة بين الرياضيين هي أن صحة الفرضية تقاس بوضوحها، فقد قبلوا الفرضيات الأربع من دون نقاش، أما الفرضية الخامسة فلم تكن واضحة لديهم، إذ أنها أعقد بكثير من الفرضيات السابقة لها، لذا ساد الاعتقاد بين الرياضيين بأن ما أسماه إقليدس فرضية خامسة، إن هي إلا مبرهنة (نظرية) تستند إلى ما قبلها من الفرضيات، وقد ظل الرياضيون في مشارق الأرض ومغاربها يجرون المحاولة تلو الأخرى للبرهان على فرضية إقليدس الخامسة قرابة ألفي سنة؛ بيد أن محاولاتهم كلها ذهبت أدراج الرياح. وقد اعتقد كثير منهم بأنهم قد أفلحوا في البرهان على هذه الفرضية ؛ إلا أنه عند التعمق في دراسة هذه البراهين، وجد أنها تحوي إما غلطة منطقية، أو فرضية أخرى مكافئة للفرضية قيد البرهان.
والفرضية المكافئة للفرضية الخامسة، والتي يحفظها الجميع هي:
«لا يمكن أن نرسم غير مستقيم واحد مواز لمستقيم مفروض من نقطة خارجة عنه». إن هذا الغموض الذي اكتنف الفرضية الخامسة في مدة تزيد على العشرين قرناً أدى إلى أن بعض العلماء أخذوا من إقليدس فرضياته الأربع الأولى، وأضافوا إليها فرضية خامسة تعاكس فرضيته الخامسة، فاكتشفوا عدم وجود تناقض بين مجموعة فرضياتهم الخمس الجديدة، مما قاد إلى:
1 - إثبات حقيقة استقلال فرضية إقليدس الخامسة عن فرضياته الأربع الأولى.
2 - اكتشاف هندسات جديدة «لا إقليدية» سميت بأسماء مكتشفيها.
من هذه الهندسات اللاإقليدية هندسة لاباتشيفسكي Lobachevisky ما بين (1792-1856) وهندسة ريمان Riemann.
الفضاء (الهندسي) الإقليدي Euclidean (geometrical) space
هو مجموعة نقاط الفضاء الهندسي العادي، أي الذي يخضع لفرضيات إقليدس.
الفضاء الإقليدي ثلاثي البعد Three Dimensional Euclidean Space
لتكن O نقطة محددة، OX, OY, OZ ثلاثة محاور متعامدة ثابتة، في الفضاء الإقليدي الهندسي، ولتكن الأشعة الثلاثة
 |
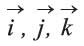(أو نكتبها i, j, k)، أطوالها |  |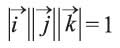
 |
|||
| الشكل (1) | |||
 |
|||
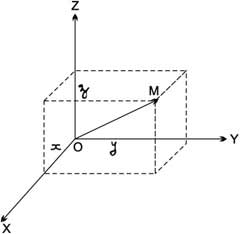
| الشكل (2) |
إن الفرضية الخامسة لإقليدس - والتي تم ذكر فرضية مكافئة لها: «لا يمكن إنشاء سوى مستقيم واحد L يوازي مستقيماً مفروضاً D من نقطة ما M خارجة عنه» - تجعل بالإمكان تعيين أي نقطة في الفضاء بإحداثياتها نسبة إلى جملة إحداثية مؤلفة من ثلاثة محاور ثابتة.
أي أن كل نقطة M من الفضاء R3 تتعين بثلاثة أعداد حقيقية x, y, z. أي يقابلها ثلاثية وحيدة (x, y, z)، حيث x, y, z هي مركبات المتجه OM على المحاور OX, OY, OZ - والعكس بالعكس (الشكل-2).
أي إنه يوجد تقابل بين نقاط الفراغ الهندسي الإقليدي المنسوب إلى جملة محاور إحداثية OXYZ وبين مجموعة الجداء الديكارتي R3 = {(x, y, z)}: x, y, z ∈ R} حيث R هي مجموعة الأعداد الحقيقية. إن هذا يجعل كل منحن أو سطح أو مجسم في R3 يمثل بعدد من المعادلات، تساعد على دراسته ومعرفة خواصه، وهذا هو مجال الهندسة التحليلية.
مثال : معادلة كرة مركزها M0 (x0, y0, z0) ونصف قطرها a هو :
(x - x0)2 +(y - y0)2 + (z - z0)2 = a2
تعريف: الفضاء الإقليدي هو فضاء حقيقي مزود بجداء داخلي.
الفضاء الحقيقي هو فضاء متجهي[ر] معرف على حقل الأعداد الحقيقية R.
الجداء الداخلي على فضاء حقيقي E هو تطبيق *: E . E → R; (u, v) → u*v يحقق الشروط الآتية:
1) (u + v) * v = u* v + w * v ∀ u, w, v ∈ E
2) v * (u + w) = v * u + v * w ∀ u, w, v ∈ E
3) (a.u) * v = a (u * v) ∀ a ∈ E; ∀ u, v ∈ E
4) (u * v) = v * u ∀ u, v ∈ E
5) u * u ≥ 0 ∀ u ∈ E
6) u = 0 ⇔ u * u = 0
الفضاء المتجهي الحقيقي (real vector space) R3
يعرف على المجموعة R3 = {(x, y, z)}: x, y, z ∈ R} عمليتي جمع، وضرب بعدد كما يأتي:
ـ حاصل جمع متجهين a (a1, a2, a3) وb (b1, b2, b3) من R3 هو متجه ثالث c = (c1, c2, c3) = (a1 + b1, a2 + b2, a3 + b3)
ـ حاصل ضرب متجه a (a1, a2, a3) من R3 بعدد حقيقي λ من R هو متجه d يوازي المتجه a ويساوي d = (.λ .a1, .λ .a2, .λ .a3).
ـ إن المجموعة R3 = {(x, y, z) : x, y, z ∈ R} مع عمليتي الجمع والضرب بعدد من R، تشكل فضاءً متجهياً حقيقياً.
الجداء الداخلي (العددي، السلمي) inner (scalar) product على R3
إذا كان a (a1, a2, a3) وb (b1, b2, b3) متجهين في فضاء متجهي حقيقيR3 فإن جداء المتجهين a (a1, a2, a3) وb (b1, b2, b3) المعرف بالشكل
a.b = (a1b1 + a2b2 + a3b3) هو جداء داخلي علىR3 .
الفضاء (المتجهي) الإقليدي Euclidean (vector) space R3
إن الفضاء المتجهي الحقيقي R3 مع عملية الجداء الداخلي السابقة، هو فضاء إقليدي.
مثال: الجداء العددي للمتجهين a (- 2, 5, 3), b (3, - 2, 1) هو
a.b = (- 2) (3) +(5) (- 2) + (3) (1) = - 13
طول متجه a (a1, a2, a3)
إن:
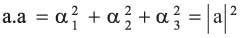(حيث |a| طول المتجه a) أي إن طول المتجه a (a1, a2, a3) هو:
 |
|
| الشكل (3) |
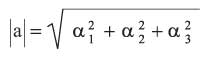
البعد بين نقطتين
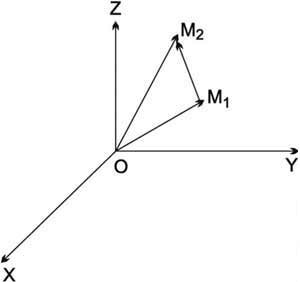
إذا كانت M1 (x1, y1, z1) وM2 (x2, y2, z2) نقطتين من الفضاء الإقليدي R3 فإن المتجه M1 M2 = OM2 - OM1 أي أن M1 M2 (x2- x1, y2- y1,z2- z1 وطول هذا المتجه هو:
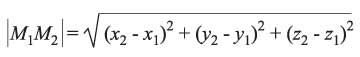
وهو البعد بين النقطتين M1 وM2 (الشكل-3).
مثال: البعد بين النقطتين M1 (-2,3,1) M2 (1,3,-3) هو:
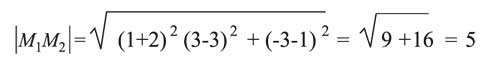
الزاوية بين متجهين
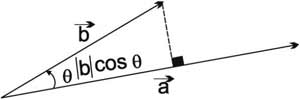
إذا كان المتجهان a (a1, a2, a3) وb (b1, b2, b3) في الفضاء الإقليدي R3 وكانت بينهما زاوية قياسها θ حيث R00 ≤ θ ≤ 1800m ، فيبرهن أن الجداء الداخلي للمتجهين a وb هو:a.b = |a|.|b|.cos θ ومن ثمَّ |cos θ = a.b / |a|.|b
 |
|
| الشكل (4) |
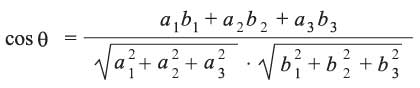
أي θ = arccos (a.b / |a|.|b|) (الشكل-4).
إن |b|.cos θ هو المسقط القائم للمتجه b على المتجه a
كذلك |a|.cos θ هو المسقط القائم للمتجه a على المتجه b
فالجداء الداخلي لمتجهين يساوي طول أحدهما مضروب بالمسقط القائم للمتجه الثاني عليه. ومن ثمَّ فإن مركبات متجه ما a على المحاور الإحداثية OX, OY, OZ هي i.a, j.a, k.a
مثال: لتكن النقاط A (1, 1, 1), B (3, 2, 3), C (0, -1, 1) فلحساب زاوية الرأس C في المثلث ABC، ولتكن θ، تحسب الزاوية بين المتجهين CA, CB
وبفرض a = CA , b = CB يكون a = OA - OC , b = OB - OC
a = (1,1,1) - (0,-1,1) = (1,2,0) وb = (3,2,3) - (0,-1,1) = (3,3,2)
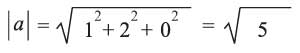و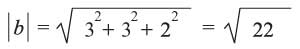a.b = (1) (3) +(2) (3) +(0) (2) = 9
وتكون
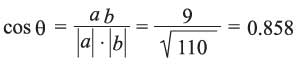
ومن ثمَّ فإن b = 30.9º = 30º 54′
تعامد متجهين
إذا كان المتجهان a ≠ o ≠ b فإن a وb متعامدان إذا كانت الزاوية θ بينهما قائمة، أي إذا كانت cos θ = 0، أي إذا كان الجداء الداخلي للمتجهين يساوي الصفر، أي a.b = 0، أي a1b1 + a2b2 + a3b3 = 0. إذا كان أحد المتجهين a أوb صفراً فإن a.b = 0.
مثال: إن أشعة القاعدة i = (1,0,0), j = (0,1,0), k = (0,0,1) في الفضاء الإقليدي R3 متعامدة مثنى مثنى، حيث إن i . j = j . k = k . j = 0وإن أي متجه
a (a1, a2, a3) من R3 يكتب منسوباً إلى أشعة القاعدة i, j, k بالشكل:
 |
|
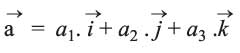
| الشكل (5) |
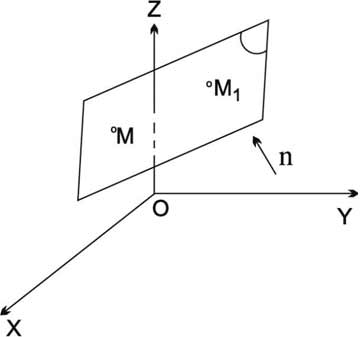
إن معادلة المستوي P المار بالنقطة M1 (x1, y1, z1) والعمودي على المتجه n (a, b, c) هي M1M.n = 0.
حيث M (x, y, z) نقطة ما من المستوي P (الشكل-5)،
أي a (x- x1) + b (y- y1) + c (z- z1) = 0 أي a x + b y + cz = d.
مثال: إن معادلة المستوي المار بالنقطة M1(-2,1,-3) والعمودي على المتجه AB حيث A (2,0,-3), B (-3, -2, 2) هي:
M(-3-2)(x +2) + (-2-0) (y-1) + (2 +3) (z+3) = 0M
M5x + 2y - 5z = 7M
الجداء المتجهي (الخارجي) vector product
الجداء المتجهي لمتجهين a (a1, a2, a3) وb (b1, b2, b3) في فضاء إقليدي R3 هو متجه
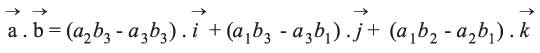
يمكن كتابته بالشكل:
 |
|
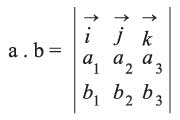
| الشكل (6) |
1) a . b = - b . a (الجداء المتجهي غير تبديلي).
2) a . (b + c) = a . b + a . c (الخاصة التوزيعية) .
3) (.(α . a) (β . b) = (α . β) (a . b وذلك أياً تكن α, β ε R
4) a , b = O إذا كان a وb متوازيين.
5) a . (λ a) = O وذلك أياً يكن a ε R3 وλ ε R.
الجداء المتجهي للأشعة i, j, k
1) i . j = k, j . k = i, k . i = j
2) j . i = - k, k . j = - i, i . k = - j
خواص المتجه P = a . b
 |
|
| الشكل (7) |
2) طول المتجه P يعطى بالعلاقة |P| = |a| . |b| . sin θ حيث θ هي الزاوية بين المتجهين a وb؛n00 ≤ θ ≤ 1800m .
3) المتجه P لا يتغير بتغير الجملة الإحداثية OXYZ.
4) مساحة متوازي الأضلاع ABCD تساوي طول الجداء الخارجي للمتجهين AB وAD (أو أي ضلعين آخرين مشتركين برأس واحد) (الشكل-7).
مثال: النقاط الثلاث A (-2,3,-1), B (2,0,-5), C (-3,-1,3) هي رؤوس مثلث ABC
لحساب مساحته يحسب الجداء الخارجي للمتجهين AB وAC
AB = (2 + 2) i + (0 - 3) j + (- 5 + 1) k = 4 i - 3 j - 4 k
AC = (- 3 + 2) i + (- 1 - 3) j + (3 + 1) k = - i - 4 j + 4 k
AB . AC = (- 12 - 16) i - (16 - 4) j + (- 16 - 3) k = - 28 i - 12 j - 19 k
إن مساحة المثلث ABC تساوي
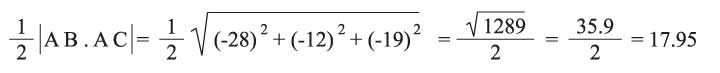
مطابقة لاغرانج
إن العلاقتين |a . b| = |a| . |b| . sin θ
و a . b = |a| . |b| . cos θ
تعطيان (a . b)2 + (|a . b|)2 = |a|2 . |b|2 أي:
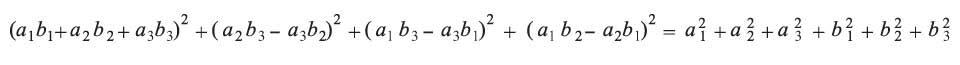
وهي ما تسمى مطابقة لاغرانج.
الجداء المختلط mixed product أو the scalar triple product
إذا كانت الأشعة الثلاث a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3) من الفضاء الإقليدي R3 فإن الجداء العددي a.(b . c) يدعى الجداء المختلط ويرمز له
(a, b, c).
خواص الجداء المختلط للأشعة a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3)
1)
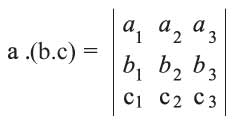
2) a . (b . c) = b . (c . a) = c . (a . b)
3) a . (c . b) = b . (a . c) = c . (b . a) = - a . (b . c)
 |
|
| الشكل (8) |
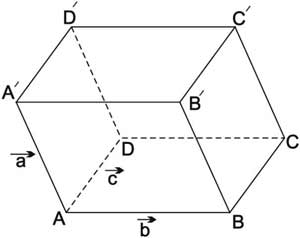
5) إذا كانت الأحرف الجانبية لمتوازي سطوح ABCDA ′B ′C ′D المنطلقة من أحد الرؤوس تساير (توازي وتساوي) الأشعة a, b, c فإن القيمة المطلقة للجداء المختلط a . (b . c) تساوي حجم متوازي السطوح ABCDA ′B ′C ′D (الشكل-8).
6) إذا كانت الأشعة الثلاث a (a1, a2, a3) وb (b1, b2, b3) وc (c1, c2, c3) واقعة في مستوٍ واحد (أو توازي مستوياً واحداً) فإن a . (b . c) = 0
معادلة مستوي يمر من ثلاث نقاط غير واقعة على استقامة واحدة
لتكن M1 (x1, y1, z1) وM2 (x2, y2, z2) وM3 (x3, y3, z3) ثلاث نقاط غير واقعة على استقامة واحدة، ولتكن M (x, y, z) نقطة ما من المستوي M1, M2, M3 فإن الأشعة M1M, M1M2, M1M3 تقع في مستو واحد، ومن ثمَّ فالجداء المختلط لها يساوي الصفر، أي
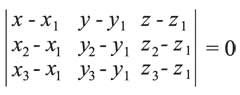
وهي معادلة المستوي الذي يمر من ثلاث نقاط غير واقعة على استقامة واحدة.
مثال: لإيجاد معادلة المستوي المار بالنقاط الثلاث A (-2,3,.-1), B (2,0,-5), C (-3,-1,3)
تؤخذ نقطة ما M (x, y, z) من هذا المستوي ثم تكتب المعادلة
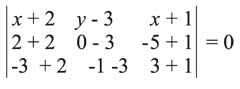
ينتج من نشر المحدد: n(-12 - 16) (x + 2) - (16 - 4) (y - 3) + (-16 -3) (z + 1) = 0
أي إن معادلة المستوي هي:
v28x + 12y + 19z = -39
أنور توفيق اللحام