اعداد طبيعيه
Natural numbers - Entiers naturels
الأعداد الطبيعية ط
يمثل اكتشاف الأعداد الطبيعية natural numbers إحدى عبقريات العقل البشري. وقد كان الغرض الرئيسي من اكتشافها هو الإجابة عن السؤال «كم؟». وقد سميت المجموعة التي توفر الإجابة عن هذا السؤال مجموعة أعداد العد counting numbers وهي {1، 2، 3،...}. ومما تجدر الإشارة إليه أن العدد «صفر» لم يكتشف إلا بعد قرون عدة من اكتشاف أعداد العد مع أنه لازم أيضاً للإجابة عن السؤال «كم؟» وقد أُطلق على المجموعة المؤلفة من أعداد العد والصفر اسم «مجموعة الأعداد الطبيعية» أو «مجموعة الأعداد الصحيحة غير السالبة».
ثمة طرائق عدة لتعريف هذه المجموعة، التي يرمز لها بـ ط، منها تلك التي تستخدم موضوعات الرياضي الإيطالي جوزيبي بيانو (1858- 1932م) Giuseppe Peano التالية:
1 ـ يوجد تطبيق تا: ط ! ط بحيث يقابل كل عنصر س من المجموعة ط وفق تا لاحقة الوحيد س+= تا (س). وهذا التطبيق متباين، أي أنه إذا كان لعنصرين س، ع من ط عنصر لاحق واحد، أي إذا كان س+= ع+ ، فإن س=ع.
2 ـ يوجد عنصر من المجموعة ط، يسمى صفراً، ونرمز له بـ \ (أو بنقطة .) لايمثل لاحقاً لأي عنصر من عناصر ط.
3 ـ كل مجموعة جزئية من ط حاوية للصفر وللاحق كل عنصر منها يجب أن تتطابق مع المجموعة ط.
لما كان لكل عنصر عنصر لاحق، فإنه يوجد عنصر لاحق للصفر، يرمز له بـ1، ويسمى واحداً. وإذا كان س+ العنصر اللاحق لِـ س، فإن س يسمى سابق س+. يوجد لكل عدد طبيعي مغاير للصفر عنصر سابق وحيد.
لإثبات هذه الدعوى، يلاحظ أولاً أنه لما كان لاحق الصفر العدد 1، أي أن \ +=1 ، فإن \ هو العنصر السابق للعدد 1. ومن جهة أخرى، فإذا وُجد لـ ن عنصر سابق فإن للعدد ن+، أي للاحق ن، عنصراً سابقاً هو ن، وهلم جراً. وهكذا فإنه يوجد لكل من الأعداد التي تلي ن عنصر سابق. ولما كان يوجد للعدد 1 عنصر سابق، فإنه يؤخذ ن = 1، وعندئذ يوجد لكل من أعداد المجموعة ط المغايرة للصفر عنصر سابق. وهذا العنصر وحيد، لأنه إذا افترض جدلاً أن ثمة عنصراً ن من ط له عنصران سابقان مختلفان ك، ل فإنه ينتج عندئذ أن ك+=ل+=ن. ويقتضي هذا استناداً إلى الموضوعة 1 أن ك= ل، وهذا خُلْفٌ (أي إن ذلك أدى إلى تناقض).
العمليات على المجموعة ط
الجمع: يمكن تعريف هذه العملية الداخلية على المجموعة ط موضوعاتياً (أي استناداً إلى عدد من الموضوعات) على نحو ينسجم مع المفهوم الحدسي للجمع. فإذا كان م، ن أي عددين طبيعيين فإنه: ن+\=ن، ن+م+=(ن+م)+. يترتب على هذا التعريف الخواص التالية:
ن+1=ن+\+=(ن+\)+=ن+ ، أي أن ن+1=ن+
وهكذا فإن لاحق عدد طبيعي هو العدد الذي يليه بالمعنى المألوف لهذا الكلام. ومن جهة أخرى، فإذا أعطي عدد طبيعي مثبت ن، فإنه ينتج أن ن+0=ن، ن+1=ن+. وإذا كانت مـ مجموعة الأعداد الطبيعية م التي يكون فيها المجموع ن+م معرفاً، أي يمكن حسابه، فإن معرفة ن+م تقتضي معرفة ن+م+=(ن+م)+=(ن+م)+1. لذا فإن المجموعة مـ تتطابق والمجموعة ط (وفق الموضوعة 3) لأنها تحوي الصفر ولأنها تحوي م+1 عند احتوائها م نظراً لأن المساواة الأخيرة تبين أن: (ن+م)+1=ن+(م+1)
تجميعية عملية الجمع: إن المساواة ن+0=ن تقتضي أن يكون:
م+(ن+0)=م+ن=(م+ن)+0 لذا فالمساواة م+(ن+هـ)=(م+ن)+هـ صحيحة عندما هـ =0، ولو افترضت صحتها لأجل هـ، فإن:
م+(ن+هـ+)=م+(ن+هـ)+=[م+(ن+هـ)]+=[(م+ن)+هـ]+=(م+ن)+هـ+
وهذا يعني أنها صحيحة أيضاً لأجل هـ+، ومن ثم فإنها صحيحة أياً كان العدد الطبيعي هـ (استناداً إلى الموضوعة3).
تبادلية عملية الجمع: يمكن إثبات هذه الخاصة على ثلاث مراحل:
ـ المساواة ن+0=0+ن. إنها صحيحة عندما ن=0، ولو افترضت صحتها لأجل ن، فإنه ينتج أن: ن++0=ن+=(ن+0)+=(0+ن)=0+ن+
لذا فإنها صحيحة لأجل ن+، ومن ثم فإنها صحيحة أياً كان العدد الطبيعي ن (الموضوعة 3).
ـ المساواة ن+1=1+ن. إنها صحيحة عندما ن=0 استناداً إلى ما سبق. ولو افترضت صحتها لأجل ن، فإنه يكون:
ن++1=(ن+1)+1=(ن+1)+=(1+ن)+=1+ن+
إذن فهي صحيحة لأجل أي عنصر ن من المجموعة ط.
ـ أخيراً المساواة ن+م=م+ن. هذه المساواة صحيحة عندما ن=0، ولو كانت صحيحة عند تثبيت م وافتراض ن عدداً طبيعياً ما، فإنه ينتج أن:
ن++م=(ن+1)+م=ن+(1+م)=ن+(م+1)
لأنه سبق وتبين أن ن+=ن+1. عندئذ ينتج استناداً إلى تجميعية عملية الجمع أن:
ن++م=(ن+م)+1=(م+ن)+1=م+(ن+1)=م+ن+
لذا فإن ن+م=م+ن مساواة صحيحة أياً كان العنصر ن من ط.
يلاحظ أن كل هذه البراهين تستند حصراً إلى موضوعات بيانو وتعريف عملية الجمع.
انتظام عملية الجمع: يفترض أن كل عنصر في المجموعة ط منتظم بالنسبة لعملية الجمع، بمعنى أن
م+ن=هـ+ ن Û م=هـ
والعنصر ن، في هذا التكافؤ المنطقي، هو العنصر المنتظم.
الضرب: تعرف عملية الضرب موضوعاتياً كما يلي: إذا كان ن، م أي عددين طبيعيين، فإن ن×0-0، ن×م+=(ن×م)+ن هذا ويرمز أحياناً للعدد ن×م بالشكل ن م.
وكما هي الحال في عملية الجمع، فإن هذين التعريفين ينسجمان مع معارفنا الحدسية، ويمكّنان ببساطة، من إيجاد جداء (أي حاصل ضرب) عددين طبيعيين. وعلى سبيل المثال، فإن
ن×1=ن×0+=ن×0+ن=0+ن=ن
أي إن ن×1=0 كذلك فمن الممكن التحقق من صحة الخواص التالية:
ـ عملية الضرب توزيعية من اليمين ومن اليسار بالنسبة لعملية الجمع:
هـ (م+ن)=هـ م+هـ ن=(م+ن) هـ=م هـ+ن هـ
ـ عملية الضرب تجميعية: ن (م هـ)=(ن م) هـ
ـ عملية الضرب تبديلية: ن م=م ن
ـ الصفر عنصر ماص absorbant في عملية الضرب، ويعني هذا أنه أياً كان العدد الطبيعي ن فإن:
\ ×ن = \
ـ جداء عددين طبيعيين غير صفريين هو عدد غير صفري:
م ن¹ 0 Û م¹0 وَن¹0
أو
م ن¹ 0 Û م ¹ 0 أو ن ¹ 0
ـ كل عدد غير صفري منتظم بالنسبة لعملية الضرب:
م ن=هـ ن Û م=هـ(ن ¹ 0)
ـ العدد 1 عنصر محايد بالنسبة لعملية الضرب:
1 ×ن = ن
بنية الترتيب للمجموعة ط
يمكن تعريف علاقة ترتيب في المجموعة ط على النحو التالي:
الشرط اللازم والكافي كي تتحقق العلاقة ن ≥ م بين عددين طبيعيين ن، م هو أن يوجد عدد طبيعي هـ بحيث يكون ن= م+هـ.
هذا ويُقرأ الرمز ن ≥ م على النحو «ن أكبر من م أو يساويه» أو اختصاراً «ن أكبر من م» (المساواة تَرِد عندما هـ=0). وينسجم هذا التعريف مع المفهوم الحدسي للمتراجحة، بمعنى أن ن يكون أكبر من م إذا كان ن مساوياً للعدد م مضافاً إليه عدد آخر. ومن جهة أخرى، فإن ≥ هي علاقة ترتيب بالمعنى الواسع، أي إنها انعكاسية ومتخالفة التناظر ومتعدية، أي إن:
آ ـ ن≥ ن، لأن ن = ن +\(خاصة الانعكاس).
ب ـ ن≥م وَ م ≥ ن Û ن = م + و وَ م = ن + هـ Ü ن = ن + هـ + و Ü هـ + و = \ Ü هـ = \ Ü ن = م
وهكذا فإنه ينتج أن المتراجحتين ن ≥ م، م ≥ ن تقتضيان المساواة ن = م (خاصة تخالف التناظر).
جـ ـ ن ≥ م Ü ن = م + هـ؛ م ≥ ر Ü م = ر + ك Ü ن = ر + (هـ + ك) Ü ن ≥ ر.
وهكذا فإن المتراجحتين ن ≥ م، م ≥ ر تقتضيان المتراجحة ن ≥ ر (خاصة التعدي).
تعرّف على المجموعة ط علاقة ترتيب > بالمعنى الضيق كذلك، إذ إنها تكون متخالفة التناظر ومتعدية فقط. وهكذا فإن الشرط اللازم والكافي كي تتحقق العلاقة ن > م بين عددين طبيعيين ن، م هو أن يوجد عدد طبيعي هـ مغاير للصفر بحيث تكون ن = م + هـ . ومن الواضح أن هذه العلاقة تشترط أن يكون هـ ¹0، ويمكن التعبير عن هذا بأن نكتب هـ э ط*، حيث ط*=ط-{0}. هذا ويقرأ الرمز ن > م على النحو «ن أكبر تماماً من م».
تنسجم علاقة الترتيب مع عمليتي الجمع والضرب في المجموعة ط، بمعنى أنه إذا كان ن، م أي عددين طبيعيين يحققان المتراجحة ن ≥ م، وكان هـ أي عدد طبيعي، فإن ن+هـ≥ م + هـ؛ ن هـ ≥ م هـ. ومن الضروري التحدث عن تحديد مايتعلق بالانسجام مع عملية الضرب في حال علاقة الترتيب بالمعنى الضيق، ذلك أن هـ عند ذلك يجب أن يكون مغايراً للصفر: هـ ¹ \، ن < م Ü ن هـ >م هـ . لكنه لو لم يكن العدد هـ معروفاً، فإن المتراجحة ن > م قد تقتضي المساواة ن هـ = م هـ، وذلك عندما يكون هـ =\
إن بنية الترتيب على المجموعة ط هي بنية ترتيب كلي، وهذا يعني أن أي عنصرين ن، م من المجموعة ط هما دوماً متقارنان، أي إنه إذا كان ن، م أي عددين طبيعيين، فإما أن يكون ن ≥ م أو أن يكون ن ≤ م.
يطلق اسم العنصر الراجح (الراجح تماماً، القاصر، القاصر تماماً) لمجموعة جزئية من المجموعة ط على كل عنصر من ط أكبر أو يساوي (أكبر تماماً، أصغر أو يساوي، أصغر تماماً) جميع عناصر المجموعة الجزئية.
إن لاحق عدد طبيعي ن هو أصغر عناصره الراجحة تماماً، وسابقه إن وجد (وهذا السابق ليس له وجود في حال الصفر) هو أكبر عناصره القاصرة تماماً. وكل مجموعة جزئية غير خالية من ط تحوي عنصراً أصغر وحيداً (وهو أصغر من جميع العناصر الأخرى). وكل مجموعة جزئية من ط غير خالية ولها عنصر راجح تحوي عنصراً أكبر وحيداً (وهو أكبر من جميع العناصر الأخرى).
يقال عن مجموعة إنها منتهية إذا وجد تقابل بينها وبين مجال[1، ن] من المجموعة ط. وعندئذ يسمى ن العدد الأصلي (أو الكاردينالي) لهذه المجموعة. وإن الاجتماع والتقاطع والجداء الديكارتي لمجموعتين منتهيتين هي مجموعات منتهية، وإذا رمزنا للعدد الأصلي لمجموعة س بالشكل عأس فإن:
عأس+عأع=عأ(سÈع)+عأ(سÇع)
قسمة الأعداد الطبيعية
إذا كان أэ ط، ب э ط، فإن أ يكون مضاعفاً للعدد ب إذا وجد عنصر ك من ط بحيث يكون أ = ب ك، أي إذا انتمى أ إلي المتتالية
طب={0، ب،2ب، 3ب،...،ن ب،...}،(ن э ط)
ويقال أيضاً إن ب يقسم أ، أو إن ب قاسم للعدد أ، ويرمز لهذا بالشكل أ/ب، ويقرأ كما يلي: «ب يقسم أ». يسمى العدد ك حاصل قسمة أ على ب، وعندئذ تكتب المساواة أ/ب=ك التي تكافئ أ = ب ك.
إن علاقة قابلية القسمة في المجموعة ط هي:
ـ انعكاسية: ذلك أن أ = أ× 1
ـ متخالفة التناظر: ذلك أنه إذا كان أ¹ \، ب ¹ \ فإن المساواتين أ=ب ك، ب=أ كَ تقتضيان أ=أ ك كَ، ومن ثم يكون ك كَ=1، لذا فإن ك=كَ=.1 إذن أ=ب.
ـ متعدية: ذلك أن أ=ب ك، ب= جـ كَ تقتضيان أ= جـ(ك كَ)، إذن جـ/أ
وهكذا فإن هذه العلاقة هي علاقة ترتيب بالمعنى الواسع. بيد أن هذا الترتيب جزئي، ذلك أنه إذا أعطي عددان طبيعيان اختياريان أ، ب، فليس من الضروري أن يقسم أ العدد ب، أو أن يقسم ب العدد أ. يفرض مثلاً أن العدد أ يقع بين عددين من المتتالية طب.
عندئذ يمكن أن يكتب أ = ب ك + ر، حيث ب > ر>\ ، والعدد ك غير صفري إذا كان أ > ب، أما إذا كان أ < ب، فإن ك= 0 ويكون أ = ر. يمكن تلخيص هذا بمتطابقة واحدة هي أ = ب ك + ر حيث ب > ر≥\ ، وذلك سواء أكان العدد ب قاسماً للعدد أ أم غير قاسم له. وفي هذه المتطابقة، يسمى ك حاصل القسمة، ر الباقي، أ المقسوم، ب القاسم (أو المقسوم عليه).
خواص القسمة:
أ ـ إذا ضرب القاسم والمقسوم بعدد واحد، فإن حاصل القسمة لا يتغير، وأما الباقي فإنه يضرب بهذا العدد. وإذا قسّم القاسم والمقسوم على عدد واحد، إن كان ذلك ممكناً، فإن حاصل القسمة لا يتغير، وأما الباقي فيقسم على هذا العدد.
ب ـ لتشكيل حاصل قسمة العدد أ على الجداء ب جـ يمكن تقسيم أ على ب، ثم تقسيم حاصل القسمة الناتج على جـ (أو بالعكس). ويمكن تعميم هذه الخاصة على قسمة عدد أ على جداء ن من العوامل، علماً بأن ترتيب عمليات القسمة اختياري ولا يؤثر في النتيجة.
جـ ـ عند تزايد المقسوم مع بقاء القاسم من دون تغيير، فإن حاصل القسمة يبقى على حاله أو يكبر.
قابلية القسمة على ط
لعدد الأولي: هو عدد مختلف عن العدد 1، ولا يقسمه إلا 1 والعدد نفسه.
والعدد المركب هو عدد من المجموعة ط لايساوي 1 وليس أولياً. وكل عدد مركب يقبل قاسماً أولياً واحداً على الأقل. والعددان الأوليان فيما بينهما هما عددان قاسمهما المشترك الوحيد هو 1.
آ ـ العدد الأولي هو أولي مع كل عدد لا يقسمه هذا العدد الأولي.
ب ـ كي يقسم عدد أولي جداء عدة عوامل أياً كان عددها، يلزم ويكفي أن يقسم واحداً منها على الأقل.
حـ ـ كي يقسم عدد أولي جُداء عدة عوامل أولية يلزم ويكفي أن يكون هذا العدد مساوياً أحد هذه العوامل.
د ـ يحلَّلُ كلُّ عدد مركب إلى جداء عوامل أولية مختلفة أو متطابقة، وهذا التحليل وحيد.
هـ ـ إذا أُعطي عددان طبيعيان أ، ب، فإن القواسم المشتركة لهما تتطابق وقواسم عدد ق هو القاسم المشترك الأكبر للعددين أ، ب، ويرمز له بالشكل ق = أ Ù ب . وإذا حلّل العددان أ، ب إلى جداء عواملهما الأولية، فإن قاسمهما المشترك الأكبر هو جداء عواملهما المشتركة بحيث يؤخذ العامل المشترك ذو القوة الأقل في التحليلين. والقاسم المشترك الأكبر للعددين أَ=أ/ق، بَ=ب/ق هو 1، وهما أوليان فيما بينهما إذ إن أ/قÙب/ق=1.
وهذه المساواة مميزة للقاسم المشترك الأكبر لعددين، ذلك أن الشرط اللازم والكافي كي يكون القاسم المشترك قَ لعددين أ، ب قاسمهما المشترك الأكبر هو أن يكون أ/قَÙب/قَ=1.
إذا ضُرب (قُسّم عند إمكان ذلك) عددان أ، ب بعدد (على عدد) ثالث ك فإن القاسم المشترك الأكبر لهما يُضْرَبُ (يُقَسَّمُ) بهذا (على هذا) العدد. أما لو ضرب (قُسّم) أحد هذين العددين بعدد (على عدد) أولي مع الآخر، فإن القاسم المشترك الأكبر للعددين أَ، ب أو للعــديين أ، بَ (أ= ك أ بفرض ك Ù ب =1 أو بَ = ك Ùب بفرض أ Ù ك =1) يساوي أ Ù ب.

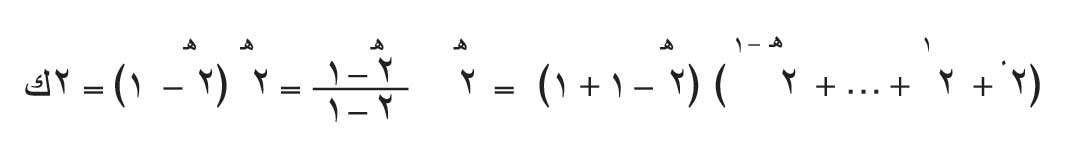
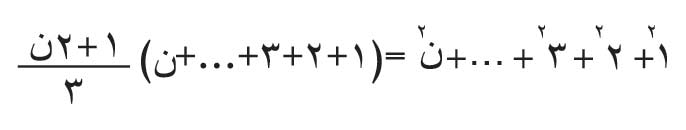
تعليق