فرز معلوماتي
Sort information - --
الفرز المعلوماتي
يعرف الفرز المعلوماتي بأنه تنظيم المعطيات بترتيب معين باستخدام برامج وخوارزميات خاصة اعتماداً على قيمة مفتاح فرز sort key. أما مفتاح الفرز فهو حقل تفرز مداخله للحصول على ترتيب مرغوب فيه للمعطيات التي تتضمن ذلك الحقل.
يمكن تعريف مسألة الفرز كما يأتي: هناك سلسلة معلومات تحوي n عنصراً، يرتبط بكلٍ من عناصرها مفتاح ينتمي إلى مجموعة مرتبة كلياً. ويُرغب في الحصول على سلسلة تكون تبديلاً لعناصر السلسلة الأصلية، بحيث تكون مفاتيح الفرز مرتبة تصاعدياً عند قراءة السلسلة من البداية إلى النهاية، وحيث مجموعة المفاتيح C هي أيُّ مجموعة مرتبة ترتيباً كلياً، أي إنها مجموعة مزودة بعلاقة £ تحقق الخواص الآتية:
" x Î C (x £ x)
" x, y Î C (x £ y) and
(y £ x) Þ x = y
" x, y, z Î C (x £ y) and
(y £ z) Þ x £ z
" x, y Î C (x £ y) or (y £ x)
يمكن، حَسَب هذا التعريف لمجموعة المفاتيح، اعتماد أيٍّ من مكونات عناصر السلسلة مفتاحاً للفرز، كما يمكن إيجاد تراكيب مختلفة من مكونات العناصر لإنشاء مفتاح للفرز. فمثلاً يمكن فرز مجموعة أشخاص حَسَب الاسم أو حَسَب العمر أو حَسَب الطول. كما يمكن اعتماد الثنائية <age, size> مفتاحاً للفرز، وتعرف علاقة الترتيب كما يأتي:
x £ y Û (x.age < y. age ) or
(x. age = y . age and x. size £ y. size)
في حالة كهذه يسمى مفتاح الفرز مفتاحاً مركباً، وتحدَّد أولوية المركبات، فنسمي المركبة الأولى مفتاحاً جزئياً أولياً، وكل من المركبات الأخرى مفتاحاً جزئياً ثانوياً. ويعدّ مفتاح الفرز فيما يلي عدداً صحيحاً، وأن السلسلة المراد فرزها هي سلسلة من الأعداد الصحيحة (العنصر يحوي المفتاح فقط)، وإن هذا الأمر لا يقلّل عمومية المسألة.
تصنيف خوارزميات الفرز ومقارنتها
يمكن تصنيف خوارزميات الفرز ضمن فئتين: الفرز الداخلي والفرز الخارجي. الأول منها هو فرز سلسلة من العناصر يمكن تخزينها في الذاكرة المركزية، أي يمكن استعمال مصفوفات أو مؤشرات لتخزين العناصر والتعامل معها. أما ثانيهما فيتعلق بفرز سلاسل كبيرة الحجم، حيث لا يمكن نسخها إلى الذاكرة المركزية؛ وهذا ما يتطلب التعامل مع ملفات. العمليات الأساسية التي تقوم بها خوارزميات الفرز هي عمليات مقارنة بين مفاتيح الفرز، وتبديل مواقع عناصر السلسلة؛ لذا تقارن خوارزميات الفرز دوماً اعتماداً على هاتين العمليتين.
آ ـ خوارزميات الفرز الداخلي
وبسبب العدد الكبير لخوارزميات الفرز الداخلي؛ يتم تصنيفها ضمن فئات تتفق فيما بينها بالمبدأ العام، ومن أمثلتها المشهورة:
1 - الفرز بالانتقاء selection sort مبدأ الفرز بالانتقاء هو البحث عن أصغر عنصر في السلسلة، ووضعه في أول موقع منها والمتابعة مع بقية عناصرها بطريقة عودية.
يبين الشكل (1) الخطوات المتتالية للفرز بالانتقاء لسلسلة تحوي ستة عناصر. في كل مرحلة يتم البحث عن أصغر عنصر، ويبدل بأول عنصر في السلسلة المُراد فرزها، ومن ثم إعادة المسألة بالطريقة ذاتها (عودياً) على العناصر المتبقية.
تُعد هذه الخوارزمية من الخوارزميات المكلفة؛ إذ يُحتاج لفرز سلسلة تحوي n عنصراً في أسوأ الأحوال إلى n2 عملية مقارنة وn عملية تبديل مواقع.
2 - الفرز بالتبديل المباشر(الفرز بطريقة الفقاعات) bubble sort بالنظر إلى خوارزمية الفرز بالانتقاء، يُلاحظ أنه لإيجاد أصغر عنصر في السلسلة، يمكن مسح السلسلة ابتداءً من نهايتيها، وتبديل العناصر المتجاورة إذا كانت لا تراعي الترتيب. في نهاية عملية المسح والتبديل هذه يكون أصغر عنصر موجوداً في بداية السلسلة، وتُطبّق الطريقة ذاتها على الجزء الباقي من السلسلة. ويعود اسم هذه الطريقة إلى صعود أخف (أصغر) العناصر إلى بداية السلسلة، كما تصعد الفقاعات إلى الأعلى في أنبوب اختبار. ويبين الشكل (2) مثالاً لها.
تُعدُّ هذه الخوارزمية أيضاً من الخوارزميات المكلفة إذ يُحتاج لفرز سلسلة تحوي n عنصراً في أسوأ الأحوال إلى n2 عملية مقارنة و n2 عملية تبديل مواقع.
3 ـ الفرز بالإدراج insertion sort: يتم في هذه الطريقة فرز قوائم تبتدئ بقائمة تحوي عنصراً وحيداً وتُبنى قائمة مرتبة أكبر منها بإدراج العناصر المراد فرزها الواحد تلو الآخر في موقعها الصحيح من هذه القائمة. ويُفترض في هذه الطريقة في الخطوة رقم i أن العناصرالـ i-1 الأولى من السلسلة مرتبة، ونوجد موقع العنصر رقم i بين هذه العناصر. يبين الشكل (3) مثالاً للفرز بطريقة الإدراج.
يمكن تحقيق هذه العملية بطرائق عدة منها: الفرز بالإدراج التسلسلي والفرز بالإدراج الثنائي.
الفرز بالإدراج التسلسلي
يكون الإدراج تسلسلياً إذا كانت عملية البحث عن موقع العنصر الجديد تجري بالتسلسل. فإذا كانت t قائمة تمثل السلسلة المراد فرزها، فإن عملية إدراج العنصر رقم i تجري بالبحث عن موقع t[i] ضمن القائمة الجزئية t[I, …,i-1] ويُبدأ من نهايتيها. تسمح هذه الطريقة بإجراء عمليات الإزاحة الضرورية لعملية الإدراج.
تُعدُّ هذه الخوارزمية أيضاً من الخوارزميات المكلفة إذ يُحتاج لفرز سلسلة تحوي n عنصراً في أسوأ الأحوال إلى n2 عملية مقارنة وn عملية تبديل مواقع.
الفرز بالإدراج الثنائي
تتميز هذه الخوارزمية من سابقتها بأنها تستفيد من كون جزء من السلسلة مرتباً من أجل إيجاد مـوقع العنصر الجديد. في المرحلة رقم i تكون السلسلة الجزئية t[1]، t[2]، ...، t[i-1] مرتبة تصاعدياً. وللبحث عن موقع العنصر t[i] فإنه يُقارن بـ t[i div 2] ويُتابع البحث في القسم الأول، أو القسم الثاني من السلسلة الجزئية حسب نتيجة المقارنة.
إن عدد تبديلات المواقع هو نفسه كما في خوارزمية الفرز بالإدراج التسـلـسلي، ولكن عدد المقارنات يتحسن تحسناً ملحوظاً (في كل عملية بحث في سلسلة جزئية طولها k يوجد log2 k عملية مقارنة فقط).
4 ـ الفرز بالدمج merge sort: وهي طريقة فرز تقوم على دمج قوائم عدة مرتبة في قائمة واحدة. يُحسب في هذه الطريقة دليل منتصف الجدول t وتُوضع القيمة الوسطى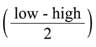 في متحول mid. ثم يُرتّب الجدول الجزئي t[low .. mid] بطريقة الفرز بالدمج. كما يُرتّب الجدول الجزئي t[mid+1 .. high] بطريقة الفرز بالدمج. ثم يُدمج الجدولان الجزئيان في جدول واحد مرتب t[low .. high].
في متحول mid. ثم يُرتّب الجدول الجزئي t[low .. mid] بطريقة الفرز بالدمج. كما يُرتّب الجدول الجزئي t[mid+1 .. high] بطريقة الفرز بالدمج. ثم يُدمج الجدولان الجزئيان في جدول واحد مرتب t[low .. high].
تُعدُّ هذه الخوارزمية من الخوارزميات الجيدة نسبياً، ويُحتاج لفرز سلسلة تحوي n عنصراً وسطياً إلى n*log n عملية مقارنة وn عملية تبديل مواقع (نسخ).
5 ـ الفرز بالتجزئة (الفرز السريع) quick sort: وهي مثال للفرز المعجمي: تُقسّم سلسلة العناصر المطلوب فرزها إلى سلسلتين جزئيتين، حيث تكون كل عناصر السلسلة الجزئية الأولى أصغر من كل عناصر السلسلة الجزئية الثانية، وتُطبق العملية ذاتها على السلسلتين الجزئيتين حتى يُحصل على سلسلة مؤلفة من عنصر واحد. لتقسيم السلسلة إلى جزأين يحققان الشرط المطلوب، يُختار أحد عناصر السلسلة ويُسمى موجّهاً pivot، وتنشأ سلسلة جزئية كلُّ عناصرها أصغر أو تساوي هذا الموجّه، وسلسلة جزئية كل عناصرها أكبر تماماً منه. إن إنشاء السلسلتين الجزئيتين على السلسلة ذاتها (من دون استعمال مصفوفة مساعدة) يؤدي إلى وضع العنصر الموجّه في المكان النهائي الذي يجب أن يبقى فيه حتى نهاية الفرز. وأخيراً تُفرز السلسلتان الجزئيتان بالطريقة العودية ذاتها.
ب ـ خوارزميات الفرز الخارجي
حين يتعذر إدخال المعطيات المراد فرزها إلى الذاكرة المركزية للحاسوب، فإن الخوارزميات التي عُرضت سابقاً تصبح غير قابلة للتطبيق. وتُواجه هذه المشكلة حين فرز معطيات كبيرة الحجم مخزَّنه في ذاكرة ثانوية؛ كالأشرطة أو الأقراص الممغنطة على صيغة ملفات تسلسلية. تتميز هذه الطريقة في التخزين بإمكانية الوصول إلى عنصر واحد فقط من عناصر الملف في أي لحظة، لذا يجب تطبيق طرائق فرز تتلاءم مع هذا الشرط الذي لم يُواجه عند فرز معطيات مخزنة في مصفوفة.
يعتمد المبدأ الأساسي في فرز الملفات على تطبيق تقنية الدمج، ويُقصد بالدمج تركيب سلسلتين مرتبتين للحصول على سلسلة مرتبة واحدة:
1 - فرز الملفات بطريقة الدمج المباشر
لفرز ملف a:
ـ يُفرّق الملف a إلى نصفين b و c
ـ يُدمج b وc وتوضع النتيجة في a. تجري عملية الدمج بتركيب عنصر من b مع عنصر مقابل من c، فيُحصل بذلك على ثنائيات مرتبة.
ـ تُعاد الخطوتان (1 و2) ولكن هذه المرة تدمج ثنائيات مرتبة من أجل الحصول على رباعيات مرتبة.
ـ تُكرر الخطوات السابقة حيث يضاعَف في كل مرة طول السلاسل المرتبة، وحتى الحصول على ملف مرتب (مؤلف من سلسلة واحدة).
يُفترض على سبيل المثال أن الملف a يحوي العناصر:
49, 99, 60, 23, 17, 11, 47, 72
ـ ينتج من عملية التفريق الملفات:
b: 49, 60, 17, 47
c: 99, 23, 11, 72
ـ ينتج دمج العناصر للحصول على ثنائيات مرتبة:
a: 49,99, 23,60, 11,17, 47,72
ـ ينتج تفريق الثنائيات المرتبة الملفين:
b: 49, 99, 11, 17
c: 23, 60, 47, 72
تعطي عملية الدمج الثانية:
a: 23, 49, 60, 99, 11, 17, 47, 72
يعطي تفريق الرباعيات المرتبة:
b: 23, 49, 60, 99
c: 11, 17, 47, 72
تعطي عملية الدمج الثالثة النتيجة المطلوبة:
a: 11, 17, 23, 47, 49, 60, 72, 99
تُسمى كل عملية تقوم بمعالجة معطيات الملف كلها مرة واحدة طوراً phase، كما تُسمى المعالجات الجزئية التي يكوّن تكرارها عملية الفرز مراحل. في المثال السابق هناك ثلاث مراحل تتضمن كل منها طورين: طور التفريق وطور الدمج.
لمّا كان طول السلاسل المرتبة المخزنة في الملف a يتضاعف في كل مرحلة، ولمّا كانت عملية الفرز تنتهي عندما يصبح طول السلاسل المرتبة مساوياً طول الملف فيُحتاج إلى log2 n خطوة. في كل خطوة هناك n عملية نسخ عناصر (يُنسخ كامل الملف).
2 - فرز الملفات بالدمج الطبيعي
لا تستفيد خوارزمية الفرز بالدمج المباشر من كون عناصر الملف الأساسي مرتبة جزئياً، ويُحصل في كل مرحلة على سلاسل مرتبة، طول كل منها ضعف طول السلاسل الناتجة من المرحلة السابقة، من دون البحث في إمكان الحصول على سلاسل أطول. في الحقيقة يمكن دمج أي سلسلتين مرتبتين طولهما n و m للحصول على سلسلة مرتبة طولها n + m. تعتمد خوارزمية الفرز بالدمج الطبيعي على المبدأ الآتي: في كل خطوة يُبحث عن أطول سلسلتين مرتبتين فتدمجا، ويُفترض فيما يلي أن المعطيات هي ملف c، يُراد فرزه بطريقة الدمج الطبيعي باستعمال ملفين مساعدين a (الشكل4).
يوضّح المثال المبين في الشكل (5) عملية الفرز بالدمج الطبيعي، حيث وضع خط تحت السلاسل المرتبة ومُثِّل محتوى الملف c قبل عملية الفرز وبعد كل مرحلة.
تنتهي عملية الفرز في المثال السابق عندما يصبح عدد السلاسل المرتبة في الملف c مساوياً الواحد.
عمار خير بيك
Sort information - --
الفرز المعلوماتي
يعرف الفرز المعلوماتي بأنه تنظيم المعطيات بترتيب معين باستخدام برامج وخوارزميات خاصة اعتماداً على قيمة مفتاح فرز sort key. أما مفتاح الفرز فهو حقل تفرز مداخله للحصول على ترتيب مرغوب فيه للمعطيات التي تتضمن ذلك الحقل.
يمكن تعريف مسألة الفرز كما يأتي: هناك سلسلة معلومات تحوي n عنصراً، يرتبط بكلٍ من عناصرها مفتاح ينتمي إلى مجموعة مرتبة كلياً. ويُرغب في الحصول على سلسلة تكون تبديلاً لعناصر السلسلة الأصلية، بحيث تكون مفاتيح الفرز مرتبة تصاعدياً عند قراءة السلسلة من البداية إلى النهاية، وحيث مجموعة المفاتيح C هي أيُّ مجموعة مرتبة ترتيباً كلياً، أي إنها مجموعة مزودة بعلاقة £ تحقق الخواص الآتية:
" x Î C (x £ x)
" x, y Î C (x £ y) and
(y £ x) Þ x = y
" x, y, z Î C (x £ y) and
(y £ z) Þ x £ z
" x, y Î C (x £ y) or (y £ x)
يمكن، حَسَب هذا التعريف لمجموعة المفاتيح، اعتماد أيٍّ من مكونات عناصر السلسلة مفتاحاً للفرز، كما يمكن إيجاد تراكيب مختلفة من مكونات العناصر لإنشاء مفتاح للفرز. فمثلاً يمكن فرز مجموعة أشخاص حَسَب الاسم أو حَسَب العمر أو حَسَب الطول. كما يمكن اعتماد الثنائية <age, size> مفتاحاً للفرز، وتعرف علاقة الترتيب كما يأتي:
x £ y Û (x.age < y. age ) or
(x. age = y . age and x. size £ y. size)
في حالة كهذه يسمى مفتاح الفرز مفتاحاً مركباً، وتحدَّد أولوية المركبات، فنسمي المركبة الأولى مفتاحاً جزئياً أولياً، وكل من المركبات الأخرى مفتاحاً جزئياً ثانوياً. ويعدّ مفتاح الفرز فيما يلي عدداً صحيحاً، وأن السلسلة المراد فرزها هي سلسلة من الأعداد الصحيحة (العنصر يحوي المفتاح فقط)، وإن هذا الأمر لا يقلّل عمومية المسألة.
تصنيف خوارزميات الفرز ومقارنتها
يمكن تصنيف خوارزميات الفرز ضمن فئتين: الفرز الداخلي والفرز الخارجي. الأول منها هو فرز سلسلة من العناصر يمكن تخزينها في الذاكرة المركزية، أي يمكن استعمال مصفوفات أو مؤشرات لتخزين العناصر والتعامل معها. أما ثانيهما فيتعلق بفرز سلاسل كبيرة الحجم، حيث لا يمكن نسخها إلى الذاكرة المركزية؛ وهذا ما يتطلب التعامل مع ملفات. العمليات الأساسية التي تقوم بها خوارزميات الفرز هي عمليات مقارنة بين مفاتيح الفرز، وتبديل مواقع عناصر السلسلة؛ لذا تقارن خوارزميات الفرز دوماً اعتماداً على هاتين العمليتين.
آ ـ خوارزميات الفرز الداخلي
وبسبب العدد الكبير لخوارزميات الفرز الداخلي؛ يتم تصنيفها ضمن فئات تتفق فيما بينها بالمبدأ العام، ومن أمثلتها المشهورة:
1 - الفرز بالانتقاء selection sort مبدأ الفرز بالانتقاء هو البحث عن أصغر عنصر في السلسلة، ووضعه في أول موقع منها والمتابعة مع بقية عناصرها بطريقة عودية.
يبين الشكل (1) الخطوات المتتالية للفرز بالانتقاء لسلسلة تحوي ستة عناصر. في كل مرحلة يتم البحث عن أصغر عنصر، ويبدل بأول عنصر في السلسلة المُراد فرزها، ومن ثم إعادة المسألة بالطريقة ذاتها (عودياً) على العناصر المتبقية.
| المعطيات | 20 | 40 | 62 | 30 | 120 | 130 | |
| الاختيار | 20 | ||||||
| 40 | 62 | 30 | 120 | 130 | 20 | ||
| الاختيار | 30 | ||||||
| 40 | 62 | 120 | 130 | 30 | 20 | ||
| الاختيار | 40 | ||||||
| 62 | 120 | 130 | 40 | 30 | 20 | ||
| الاختيار | 62 | ||||||
| 120 | 130 | 62 | 40 | 30 | 20 | ||
| الاختيار | 120 | ||||||
| 130 | 120 | 62 | 40 | 30 | 20 | ||
| الشكل (1) مثال للفرز بالانتقاء | |||||||
2 - الفرز بالتبديل المباشر(الفرز بطريقة الفقاعات) bubble sort بالنظر إلى خوارزمية الفرز بالانتقاء، يُلاحظ أنه لإيجاد أصغر عنصر في السلسلة، يمكن مسح السلسلة ابتداءً من نهايتيها، وتبديل العناصر المتجاورة إذا كانت لا تراعي الترتيب. في نهاية عملية المسح والتبديل هذه يكون أصغر عنصر موجوداً في بداية السلسلة، وتُطبّق الطريقة ذاتها على الجزء الباقي من السلسلة. ويعود اسم هذه الطريقة إلى صعود أخف (أصغر) العناصر إلى بداية السلسلة، كما تصعد الفقاعات إلى الأعلى في أنبوب اختبار. ويبين الشكل (2) مثالاً لها.
| المعطيات | 20 | 40 | 62 | 30 | 12 | 13 | |||||||||||
| التبادل | 40 | « | 20 | ||||||||||||||
| 62 | « | 20 | |||||||||||||||
| 30 | « | 20 | |||||||||||||||
| 12 | « | 20 | |||||||||||||||
| 13 | « | 20 | |||||||||||||||
| المعطيات | 40 | 62 | 30 | 12 | 13 | 20 | |||||||||||
| التبادل | 62 | « | 40 | ||||||||||||||
| 12 | « | 30 | |||||||||||||||
| 13 | « | 30 | |||||||||||||||
| المعطيات | 62 | 40 | 12 | 13 | 30 | 20 | |||||||||||
| التبادل | 12 | « | 40 | ||||||||||||||
| 13 | « | 40 | |||||||||||||||
| المعطيات | 62 | 12 | 13 | 40 | 30 | 20 | |||||||||||
| التبادل | 12 | « | 62 | ||||||||||||||
| 13 | « | 62 | |||||||||||||||
| المعطيات | 12 | 13 | 62 | 40 | 30 | 20 | |||||||||||
| التبادل | 13 | « | 12 | ||||||||||||||
| المعطيات | 13 | 12 | 62 | 30 | 20 | ||||||||||||
| الشكل (2) مثال للفرز بطريقة الفقاعات | |||||||||||||||||
3 ـ الفرز بالإدراج insertion sort: يتم في هذه الطريقة فرز قوائم تبتدئ بقائمة تحوي عنصراً وحيداً وتُبنى قائمة مرتبة أكبر منها بإدراج العناصر المراد فرزها الواحد تلو الآخر في موقعها الصحيح من هذه القائمة. ويُفترض في هذه الطريقة في الخطوة رقم i أن العناصرالـ i-1 الأولى من السلسلة مرتبة، ونوجد موقع العنصر رقم i بين هذه العناصر. يبين الشكل (3) مثالاً للفرز بطريقة الإدراج.
| 20 | 40 | 62 | 30 | 12 | 13 | |||||
| 20 | 40 | 62 | 30 | 130 | 120 | |||||
| 20 | 40 | 62 | 13 | 120 | 30 | |||||
| 20 | 40 | 13 | 120 | 62 | 30 | |||||
| 20 | 13 | 120 | 62 | 40 | 30 | |||||
| 13 | 120 | 62 | 40 | 30 | 20 | |||||
| الشكل (3) مبدأ الفرز بالإدراج | ||||||||||
الفرز بالإدراج التسلسلي
يكون الإدراج تسلسلياً إذا كانت عملية البحث عن موقع العنصر الجديد تجري بالتسلسل. فإذا كانت t قائمة تمثل السلسلة المراد فرزها، فإن عملية إدراج العنصر رقم i تجري بالبحث عن موقع t[i] ضمن القائمة الجزئية t[I, …,i-1] ويُبدأ من نهايتيها. تسمح هذه الطريقة بإجراء عمليات الإزاحة الضرورية لعملية الإدراج.
تُعدُّ هذه الخوارزمية أيضاً من الخوارزميات المكلفة إذ يُحتاج لفرز سلسلة تحوي n عنصراً في أسوأ الأحوال إلى n2 عملية مقارنة وn عملية تبديل مواقع.
الفرز بالإدراج الثنائي
تتميز هذه الخوارزمية من سابقتها بأنها تستفيد من كون جزء من السلسلة مرتباً من أجل إيجاد مـوقع العنصر الجديد. في المرحلة رقم i تكون السلسلة الجزئية t[1]، t[2]، ...، t[i-1] مرتبة تصاعدياً. وللبحث عن موقع العنصر t[i] فإنه يُقارن بـ t[i div 2] ويُتابع البحث في القسم الأول، أو القسم الثاني من السلسلة الجزئية حسب نتيجة المقارنة.
إن عدد تبديلات المواقع هو نفسه كما في خوارزمية الفرز بالإدراج التسـلـسلي، ولكن عدد المقارنات يتحسن تحسناً ملحوظاً (في كل عملية بحث في سلسلة جزئية طولها k يوجد log2 k عملية مقارنة فقط).
4 ـ الفرز بالدمج merge sort: وهي طريقة فرز تقوم على دمج قوائم عدة مرتبة في قائمة واحدة. يُحسب في هذه الطريقة دليل منتصف الجدول t وتُوضع القيمة الوسطى
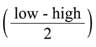 في متحول mid. ثم يُرتّب الجدول الجزئي t[low .. mid] بطريقة الفرز بالدمج. كما يُرتّب الجدول الجزئي t[mid+1 .. high] بطريقة الفرز بالدمج. ثم يُدمج الجدولان الجزئيان في جدول واحد مرتب t[low .. high].
في متحول mid. ثم يُرتّب الجدول الجزئي t[low .. mid] بطريقة الفرز بالدمج. كما يُرتّب الجدول الجزئي t[mid+1 .. high] بطريقة الفرز بالدمج. ثم يُدمج الجدولان الجزئيان في جدول واحد مرتب t[low .. high].تُعدُّ هذه الخوارزمية من الخوارزميات الجيدة نسبياً، ويُحتاج لفرز سلسلة تحوي n عنصراً وسطياً إلى n*log n عملية مقارنة وn عملية تبديل مواقع (نسخ).
5 ـ الفرز بالتجزئة (الفرز السريع) quick sort: وهي مثال للفرز المعجمي: تُقسّم سلسلة العناصر المطلوب فرزها إلى سلسلتين جزئيتين، حيث تكون كل عناصر السلسلة الجزئية الأولى أصغر من كل عناصر السلسلة الجزئية الثانية، وتُطبق العملية ذاتها على السلسلتين الجزئيتين حتى يُحصل على سلسلة مؤلفة من عنصر واحد. لتقسيم السلسلة إلى جزأين يحققان الشرط المطلوب، يُختار أحد عناصر السلسلة ويُسمى موجّهاً pivot، وتنشأ سلسلة جزئية كلُّ عناصرها أصغر أو تساوي هذا الموجّه، وسلسلة جزئية كل عناصرها أكبر تماماً منه. إن إنشاء السلسلتين الجزئيتين على السلسلة ذاتها (من دون استعمال مصفوفة مساعدة) يؤدي إلى وضع العنصر الموجّه في المكان النهائي الذي يجب أن يبقى فيه حتى نهاية الفرز. وأخيراً تُفرز السلسلتان الجزئيتان بالطريقة العودية ذاتها.
ب ـ خوارزميات الفرز الخارجي
حين يتعذر إدخال المعطيات المراد فرزها إلى الذاكرة المركزية للحاسوب، فإن الخوارزميات التي عُرضت سابقاً تصبح غير قابلة للتطبيق. وتُواجه هذه المشكلة حين فرز معطيات كبيرة الحجم مخزَّنه في ذاكرة ثانوية؛ كالأشرطة أو الأقراص الممغنطة على صيغة ملفات تسلسلية. تتميز هذه الطريقة في التخزين بإمكانية الوصول إلى عنصر واحد فقط من عناصر الملف في أي لحظة، لذا يجب تطبيق طرائق فرز تتلاءم مع هذا الشرط الذي لم يُواجه عند فرز معطيات مخزنة في مصفوفة.
يعتمد المبدأ الأساسي في فرز الملفات على تطبيق تقنية الدمج، ويُقصد بالدمج تركيب سلسلتين مرتبتين للحصول على سلسلة مرتبة واحدة:
1 - فرز الملفات بطريقة الدمج المباشر
لفرز ملف a:
ـ يُفرّق الملف a إلى نصفين b و c
ـ يُدمج b وc وتوضع النتيجة في a. تجري عملية الدمج بتركيب عنصر من b مع عنصر مقابل من c، فيُحصل بذلك على ثنائيات مرتبة.
ـ تُعاد الخطوتان (1 و2) ولكن هذه المرة تدمج ثنائيات مرتبة من أجل الحصول على رباعيات مرتبة.
ـ تُكرر الخطوات السابقة حيث يضاعَف في كل مرة طول السلاسل المرتبة، وحتى الحصول على ملف مرتب (مؤلف من سلسلة واحدة).
يُفترض على سبيل المثال أن الملف a يحوي العناصر:
49, 99, 60, 23, 17, 11, 47, 72
ـ ينتج من عملية التفريق الملفات:
b: 49, 60, 17, 47
c: 99, 23, 11, 72
ـ ينتج دمج العناصر للحصول على ثنائيات مرتبة:
a: 49,99, 23,60, 11,17, 47,72
ـ ينتج تفريق الثنائيات المرتبة الملفين:
b: 49, 99, 11, 17
c: 23, 60, 47, 72
تعطي عملية الدمج الثانية:
a: 23, 49, 60, 99, 11, 17, 47, 72
يعطي تفريق الرباعيات المرتبة:
b: 23, 49, 60, 99
c: 11, 17, 47, 72
تعطي عملية الدمج الثالثة النتيجة المطلوبة:
a: 11, 17, 23, 47, 49, 60, 72, 99
تُسمى كل عملية تقوم بمعالجة معطيات الملف كلها مرة واحدة طوراً phase، كما تُسمى المعالجات الجزئية التي يكوّن تكرارها عملية الفرز مراحل. في المثال السابق هناك ثلاث مراحل تتضمن كل منها طورين: طور التفريق وطور الدمج.
لمّا كان طول السلاسل المرتبة المخزنة في الملف a يتضاعف في كل مرحلة، ولمّا كانت عملية الفرز تنتهي عندما يصبح طول السلاسل المرتبة مساوياً طول الملف فيُحتاج إلى log2 n خطوة. في كل خطوة هناك n عملية نسخ عناصر (يُنسخ كامل الملف).
2 - فرز الملفات بالدمج الطبيعي
لا تستفيد خوارزمية الفرز بالدمج المباشر من كون عناصر الملف الأساسي مرتبة جزئياً، ويُحصل في كل مرحلة على سلاسل مرتبة، طول كل منها ضعف طول السلاسل الناتجة من المرحلة السابقة، من دون البحث في إمكان الحصول على سلاسل أطول. في الحقيقة يمكن دمج أي سلسلتين مرتبتين طولهما n و m للحصول على سلسلة مرتبة طولها n + m. تعتمد خوارزمية الفرز بالدمج الطبيعي على المبدأ الآتي: في كل خطوة يُبحث عن أطول سلسلتين مرتبتين فتدمجا، ويُفترض فيما يلي أن المعطيات هي ملف c، يُراد فرزه بطريقة الدمج الطبيعي باستعمال ملفين مساعدين a (الشكل4).
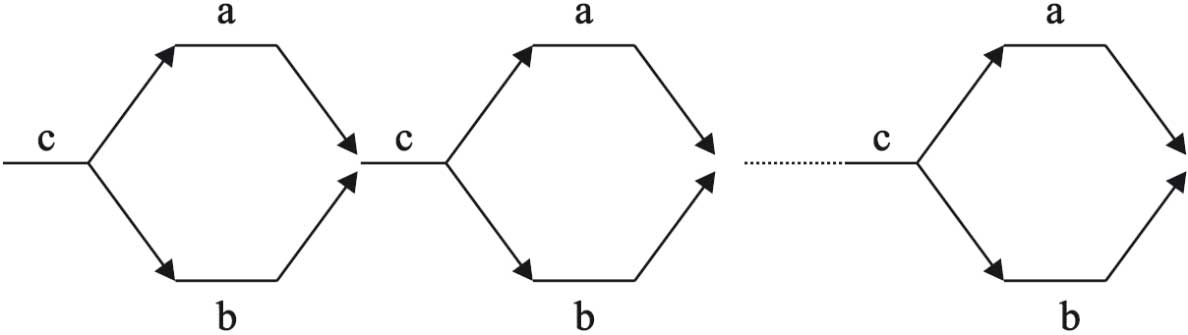 |
| الشكل (4) مبدأ الفرز بالدمج |
تنتهي عملية الفرز في المثال السابق عندما يصبح عدد السلاسل المرتبة في الملف c مساوياً الواحد.
| 10 30 5 60 11 40 42 65 12 20 25 45 17 70 2 15 52 32 9 | (1) |
| 5 10 30 60 11 12 20 25 40 42 45 65 1 2 7 15 52 70 32 92 | (2) |
| 5 10 11 12 20 25 30 40 42 45 65 65 1 2 7 15 32 52 70 92 | (3) |
| 1 2 5 7 10 11 12 15 20 25 30 32 40 42 45 52 60 65 70 92 | (4) |
| الشكل (5) مبدأ الفرز بالدمج | |
