تويت
حدانيه ( قانون)
Binomial distribution - Loi binomiale
الحدّانية (قانون -)
قانون الحدانية أو التوزيع الثنائي binomial distribution في الاحتمالات، هو القانون الذي يعطي حساب احتمال أن يكون عدد مرات النجاح في الحصول على نتيجة معينة ر مرة عندما تكرر تلك التجربة ن مرة (ن £ ر)، وحيث يكون احتمال النجاح في الحصول على النتيجة المذكورة ثابتاً في كل تكرار.
التجربة البرنولية: يطلق على أي تجربة عشوائية لها نتيجتان اسم تجربة برنولية (نسبة إلى جاك برنولي). وثمة أمثلة كثيرة في الحياة العملية على التجربة البرنولية منها:
- قذف قطعة نقود في لعبة الطرة والنقش، فلهذه التجربة الناتجان: طرة، نقش.
- إطلاق صاروخ نحو هدف معين ، تجربة لها ناتجان: النجاح إذا أصاب الصاروخ الهدف، والإخفاق إذا لم يصبه.
- وإذا أجريت تجربة عشوائية ما، وعُدّ وقوع حدث معين نجاحاً، وعدم وقوعه إخفاقاً، فإن لهذه التجربة، عملياً ودراسياً، ناتجان اثنان النجاح والإخفاق. وقد اصطلح على أن تسمى إحدى نتيجتي أي تجربة برنولية نجاحاً، وتسمى الأخرى إخفاقاً.
التجربة الحدانية وقانون الحدانية: هي تجربة عشوائية تنشأ عن تكرارات مستقلة لتجربة برنولية (ن مرة مثلاً)، وحيث يكون احتمال النجاح ثابتاً في كل تكرار، ويساوي جـ، وغايتها أو هدفها رصد النجاحات التي يمكن الحصول عليها واحتمالاتها.
من أمثلة التجارب الحدانية:
- تجربة قذف قطعة النقود في لعبة الطرة والنقش، عدداً من المرات، ن مرة مثلاً، ورصد عدد مرات الحصول على الطرة.
- سحب ن كرة، واحدة تلو الأخرى مع الإرجاع، من صندوق فيه كرات بيض وكرات سوداء، ثم رصد عدد الكرات البيضاء التي يمكن الحصول عليها بعد الانتهاء من السحب الأخير.
ويرتبط عادة بالتجربة المركبة (من ن تكراراً لتجربة برنولية) دالة تقرن كل نتيجة من نتائجها بعدد النجاحات فيها، فهي تلك الدالة التي تعد النجاحات، ويرمز لها بالرمز عا، وتسمى المتغير العشوائي الحداني، ومجموعة قيمها هي {0،1،2،....،ن}.
ينص قانون الحـدانية على أن احتمـال أن يكون عدد النجاحات مســاوياً ر نجاحاً في ن تكراراً، لتجربة برنولية هو أمثــال سر في منشـور ثنائي الحد (د + جـ س)ن حيث يكون جـ احتمال النجاح ويكون د = 1جـ (ومن هنا أخذ هذا القانون اسمه، من صلته بمنشور ثنائي الحد).
- إذا رمز لاحتمال أن يأخذ عدد النجاحات، عا، القيمة ر بالرمزحت = [عا = ر] فإن:
والجدول التالي المؤلف من سطرين، أولهما لقيم المتغير العشوائي عا: عدد النجاحات، والثاني للاحتمالات المناظرة لها، يسمى جدول قانون الحدانية أو جدول التوزيع الثنائي ذي المعلمتين أو الوسيطين ن، جـ:
يمكن استناداً إلى ما سبق أن يكتب جدول قانون الحدانية من أجل ن = 3 واحتمال نجاح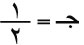 
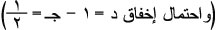، وذلك بملاحظة أن:
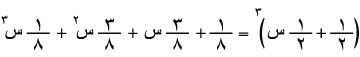
وعندئذ يأخذ الجدول الشكل الآتي:
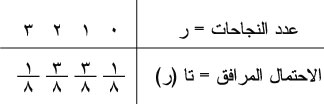
وهو جدول قانون المتغير العشوائي عا المرتبط بتكرار قذف نقود متوازنة ثلاث مرات، وحيث يدل عا على عدد مرات الحصول على الطرة مثلاً.
ملاحظات
1ـ في حالة ن =1 يكون جدول القانون الحداني
ويسمى جدول قانون برنولي ذي الوسيط جـ، ويسمى عا في هذه الحالة المتغير العشوائي البرنولي ذي الوسيط جـ.
يبرهن أن كل متغير عشوائي حداني وسيطاه: ن، جـ هو مجموع ن من المتغيرات العشوائية البرنولية المستقلة والتي وسيط كل منها حـ.
2ـ بالتمعن في جدول الحدانية، أي جدول التوزيع الحداني، يُرى أنه يتحدد بمعلومية ن وجـ، بمعنى أنه بمعرفة هاتين القيمتين يمكن معرفة جميع القيم التي يمكن أن يأخذها المتغير العشوائي الحداني عا، واحتمال كل منها:
توقع المتغير الحداني أو متوسطه = ن جـ
ذلك أن:
تباين المتغير الحداني = ن جـ د.
وسيكون انحراف المعياري
، والدالة المولدة لعزومه:
س ¬ عزعا (س) = (د + جـ eس)ن
يسمى المتغير العشوائي # متوسط النجاحات أو تواترها، وسيكون توقعه مساوياً جـ، وتباينه مساوياً
3ـ طريقة لحساب أر = حت [عا=ر]
ـ يبرهن باستخدام دستور تدريجي أن:
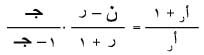
يمكن استخدام هذه الصيغة لحساب أ1، أ2،...، بعد معرفة أ.
فمثلاً من أجل ن = 6 و جـ = 0.4 يكون د = 0.6 ويكون:
أ0 = د6 = 0.0467، أ1 = 0.1866، أ2 = 0.3110، أ3 = 0.2765، ...
وهكذا يمكن حساب حت [عا ³ 3] = أ0 + أ1 + أ2 + أ3 = 0.8208.
ـ باستخدام الجداول الإحصائية
هناك جداول كثيرة تساعد في حساب الاحتمالات المطلوبة، منها:
أ ـ جداول قانون الحدانية: وذلك من أجل قيم مختلفة لـ ن ، جـ.
ب ـ جداول قانون بواسون: وتستخدم لإيجاد قيم تقريبية للاحتمالات المطلوبة، وذلك من أجل قيم لـ ن كبيرة (مثلاً ن£ 50) وجـ صغيرة (مثلاً جـ = 0.1) وضمن الشرط ن جـ ³ 5 ذلك لأن:
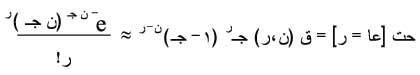
حيث ترمز ر! إلى الجداء 1× 2×3× … × ر
ثم إن حساب المقدار الأخير أسهل من حساب سابقه. إن جداول بواسون تتبع وسيطاً واحداً، ل، بينما جداول الحدانية لها وسيطان ن، جـ
يسمى التقريب السابق تقريب بواسون للتوزيع الحداني.
جـ ـ جداول التوزيع الطبيعي: وتستخدم لإيجاد قيم تقريبية للاحتمالات المطلوبة عندما تكون ن كبيرة (ن50£) وجـ لاصغيــرة جــداً ولاكبيرة جـداً و ن جـ 5³.
قانون الأعداد الكبيرة والتجربة الحدانية
يقوم التعريف الإحصائي للاحتمال على الفرض الآتي: إذا ظهرت، في ن تكراراً من التكرارات المستقلة لتجربة عشوائية، والتي تجري تحت شروط متطابقة، حادثةٌ معينة أ، احتمالها حـ، عدداً من المرات يساوي لن، وكانت ن كبيرةً جداً، فينبغي أن يكون التكرار النسبي لظهور الحادثة أ، وهو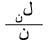
، قريباً جداً من جـ. ويلاحظ هنا أن لن ما هو إلا عدد النجاحات التي يمكن الحصول عليها في التجربة الحدانية الموصوفة والمستقلة بالحدث أ، وهكذا يكون 
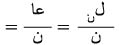متوسط عدد النجاحات، حيث يكون عا المتغير العشوائي الحداني الذي يدل على عدد النجاحات في ن تكراراً، وحيث أن توقع 
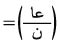وتباينه = 
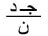، واستناداً إلى متباينة تشبيشيف يكون أياً كان هـ > 0، فإن حت 
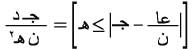وهذا يعني أنه عندما تزداد ن بلا تناه فإن احتمال أن يحيد متوسط عدد النجاحات 
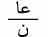عن احتمال الحدث أ بأكثر من عدد حقيقي معطى سلفاً ينتهي إلى الصفر
أنيس كنجو
Binomial distribution - Loi binomiale
الحدّانية (قانون -)
قانون الحدانية أو التوزيع الثنائي binomial distribution في الاحتمالات، هو القانون الذي يعطي حساب احتمال أن يكون عدد مرات النجاح في الحصول على نتيجة معينة ر مرة عندما تكرر تلك التجربة ن مرة (ن £ ر)، وحيث يكون احتمال النجاح في الحصول على النتيجة المذكورة ثابتاً في كل تكرار.
التجربة البرنولية: يطلق على أي تجربة عشوائية لها نتيجتان اسم تجربة برنولية (نسبة إلى جاك برنولي). وثمة أمثلة كثيرة في الحياة العملية على التجربة البرنولية منها:
- قذف قطعة نقود في لعبة الطرة والنقش، فلهذه التجربة الناتجان: طرة، نقش.
- إطلاق صاروخ نحو هدف معين ، تجربة لها ناتجان: النجاح إذا أصاب الصاروخ الهدف، والإخفاق إذا لم يصبه.
- وإذا أجريت تجربة عشوائية ما، وعُدّ وقوع حدث معين نجاحاً، وعدم وقوعه إخفاقاً، فإن لهذه التجربة، عملياً ودراسياً، ناتجان اثنان النجاح والإخفاق. وقد اصطلح على أن تسمى إحدى نتيجتي أي تجربة برنولية نجاحاً، وتسمى الأخرى إخفاقاً.
التجربة الحدانية وقانون الحدانية: هي تجربة عشوائية تنشأ عن تكرارات مستقلة لتجربة برنولية (ن مرة مثلاً)، وحيث يكون احتمال النجاح ثابتاً في كل تكرار، ويساوي جـ، وغايتها أو هدفها رصد النجاحات التي يمكن الحصول عليها واحتمالاتها.
من أمثلة التجارب الحدانية:
- تجربة قذف قطعة النقود في لعبة الطرة والنقش، عدداً من المرات، ن مرة مثلاً، ورصد عدد مرات الحصول على الطرة.
- سحب ن كرة، واحدة تلو الأخرى مع الإرجاع، من صندوق فيه كرات بيض وكرات سوداء، ثم رصد عدد الكرات البيضاء التي يمكن الحصول عليها بعد الانتهاء من السحب الأخير.
ويرتبط عادة بالتجربة المركبة (من ن تكراراً لتجربة برنولية) دالة تقرن كل نتيجة من نتائجها بعدد النجاحات فيها، فهي تلك الدالة التي تعد النجاحات، ويرمز لها بالرمز عا، وتسمى المتغير العشوائي الحداني، ومجموعة قيمها هي {0،1،2،....،ن}.
ينص قانون الحـدانية على أن احتمـال أن يكون عدد النجاحات مســاوياً ر نجاحاً في ن تكراراً، لتجربة برنولية هو أمثــال سر في منشـور ثنائي الحد (د + جـ س)ن حيث يكون جـ احتمال النجاح ويكون د = 1جـ (ومن هنا أخذ هذا القانون اسمه، من صلته بمنشور ثنائي الحد).
- إذا رمز لاحتمال أن يأخذ عدد النجاحات، عا، القيمة ر بالرمزحت = [عا = ر] فإن:
 |
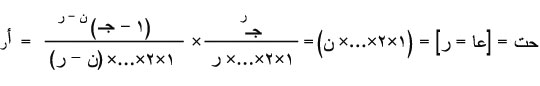| ر | 0 | 1 | 2 | .... | ر | .... | ن |
| تا(ر) | أ0 | أ1 | أ2 | .... | أر | .... | أن |
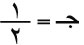
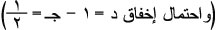، وذلك بملاحظة أن: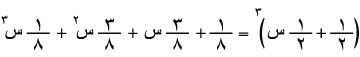وعندئذ يأخذ الجدول الشكل الآتي:
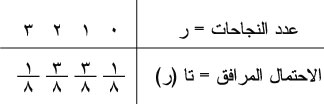
وهو جدول قانون المتغير العشوائي عا المرتبط بتكرار قذف نقود متوازنة ثلاث مرات، وحيث يدل عا على عدد مرات الحصول على الطرة مثلاً.
ملاحظات
1ـ في حالة ن =1 يكون جدول القانون الحداني
| ر | 0 | 1 |
| تا(ر) | د | جـ |
يبرهن أن كل متغير عشوائي حداني وسيطاه: ن، جـ هو مجموع ن من المتغيرات العشوائية البرنولية المستقلة والتي وسيط كل منها حـ.
2ـ بالتمعن في جدول الحدانية، أي جدول التوزيع الحداني، يُرى أنه يتحدد بمعلومية ن وجـ، بمعنى أنه بمعرفة هاتين القيمتين يمكن معرفة جميع القيم التي يمكن أن يأخذها المتغير العشوائي الحداني عا، واحتمال كل منها:
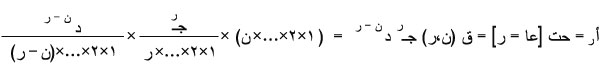
توقع المتغير الحداني أو متوسطه = ن جـ
ذلك أن:
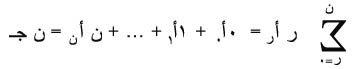
تباين المتغير الحداني = ن جـ د.
وسيكون انحراف المعياري
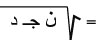، والدالة المولدة لعزومه:س ¬ عزعا (س) = (د + جـ eس)ن
يسمى المتغير العشوائي # متوسط النجاحات أو تواترها، وسيكون توقعه مساوياً جـ، وتباينه مساوياً
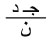
3ـ طريقة لحساب أر = حت [عا=ر]
ـ يبرهن باستخدام دستور تدريجي أن:
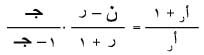
يمكن استخدام هذه الصيغة لحساب أ1، أ2،...، بعد معرفة أ.
فمثلاً من أجل ن = 6 و جـ = 0.4 يكون د = 0.6 ويكون:
أ0 = د6 = 0.0467، أ1 = 0.1866، أ2 = 0.3110، أ3 = 0.2765، ...
وهكذا يمكن حساب حت [عا ³ 3] = أ0 + أ1 + أ2 + أ3 = 0.8208.
ـ باستخدام الجداول الإحصائية
هناك جداول كثيرة تساعد في حساب الاحتمالات المطلوبة، منها:
أ ـ جداول قانون الحدانية: وذلك من أجل قيم مختلفة لـ ن ، جـ.
ب ـ جداول قانون بواسون: وتستخدم لإيجاد قيم تقريبية للاحتمالات المطلوبة، وذلك من أجل قيم لـ ن كبيرة (مثلاً ن£ 50) وجـ صغيرة (مثلاً جـ = 0.1) وضمن الشرط ن جـ ³ 5 ذلك لأن:
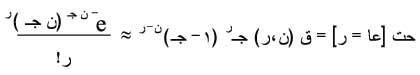
حيث ترمز ر! إلى الجداء 1× 2×3× … × ر
ثم إن حساب المقدار الأخير أسهل من حساب سابقه. إن جداول بواسون تتبع وسيطاً واحداً، ل، بينما جداول الحدانية لها وسيطان ن، جـ
يسمى التقريب السابق تقريب بواسون للتوزيع الحداني.
جـ ـ جداول التوزيع الطبيعي: وتستخدم لإيجاد قيم تقريبية للاحتمالات المطلوبة عندما تكون ن كبيرة (ن50£) وجـ لاصغيــرة جــداً ولاكبيرة جـداً و ن جـ 5³.
قانون الأعداد الكبيرة والتجربة الحدانية
يقوم التعريف الإحصائي للاحتمال على الفرض الآتي: إذا ظهرت، في ن تكراراً من التكرارات المستقلة لتجربة عشوائية، والتي تجري تحت شروط متطابقة، حادثةٌ معينة أ، احتمالها حـ، عدداً من المرات يساوي لن، وكانت ن كبيرةً جداً، فينبغي أن يكون التكرار النسبي لظهور الحادثة أ، وهو
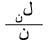، قريباً جداً من جـ. ويلاحظ هنا أن لن ما هو إلا عدد النجاحات التي يمكن الحصول عليها في التجربة الحدانية الموصوفة والمستقلة بالحدث أ، وهكذا يكون 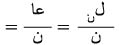متوسط عدد النجاحات، حيث يكون عا المتغير العشوائي الحداني الذي يدل على عدد النجاحات في ن تكراراً، وحيث أن توقع 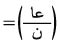وتباينه = 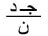، واستناداً إلى متباينة تشبيشيف يكون أياً كان هـ > 0، فإن حت 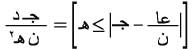وهذا يعني أنه عندما تزداد ن بلا تناه فإن احتمال أن يحيد متوسط عدد النجاحات 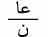عن احتمال الحدث أ بأكثر من عدد حقيقي معطى سلفاً ينتهي إلى الصفرأنيس كنجو