جاذبيه
Gravitation - Gravitation
الجاذبية
الجاذبية gravitation خاصية من خصائص المادة (والطاقة، بموجب نظرية النسبية) تتجلى بقوة تجاذبٍ يحدث فيما بين أجزائها، مهما كانت صغيرة أو كبيرة ومهما كانت المسافات الفاصلة فيما بينها، فهي إذن قوة واسعة الشمول.
قانون نيوتن العام في الجاذبية
يرى نيوتن أن هذا التجاذب بين نقطتين ماديتين، كتلتاهما ك1 وك2، نابع من قوة ق، تتناسب طردياً مع كل من الكتلتين وعكساً مع م2، ومحمولة على المستقيم الواصل بينهما أي إن الكتلة النقطية ك1 تخضع، من جراء وجود الكتلة النقطية ك2 ع لى المسافة م منها، لـ قوة ق تستجيب للعلاقة:
لى المسافة م منها، لـ قوة ق تستجيب للعلاقة:
حيث:
وعلى هذا، فإن أي كتلة مادية، من بين مجموعة كتل موزعة بأي شكل كان، تعاني لدى تحررها من كل قيد آخر، تسارعاً يتناسب عكسياً مع الكتلة المتحركة. فيقال عن الفضاء المحيط بمجموعة الكتل إنه مسرح حقل تجاذبي.
حظي قانون نيوتن هذا بشواهد تجريبية ذات دقة عالية؛ وقد يكون أهمها ما تبين من أنه يفسر تفسيراً جيداً قوانين كبلر Kepler في الميكانيك السماوي، فهو يتيح مثلاً، تعيين مواقع الكواكب في المنظومة الشمسية بفرق ٍبين الموقع المقيس والموقع المحسوب بوساطته وباستخدام قوانين نيوتن التحريكية، لا يزيد على عُشر ثانية قوسية وعلى مدى عشرات الدورات الكوكبية أو مئاتها، ولم يشذ عن هذا القانون سوى عطارد، وبمقدار أقل الزُّهرة والأرض (وهي كواكب خفيفة أقرب إلى الشمس، وقد أمكن تفسير هذا الشذوذ الضعيف في إطار نظرية النسبية العامة، كما سيُرى بعد قليل).
ثمة شاهد إضافي على عمومية هذا القانون في علم الفلك وهو «الحركة النسبية للنجوم الثنائية» étoiles doubles إذ يدور كل نجم حول رفيقه وفق إهليلج (قطع ناقص) يستجيب لقوانين كبلر، وهي نتيجة لقوانين نيوتن، وهنا أيضاً تشذ عن هذا القانون الثنائية العظيمة الكتلة شذوذاً تفسره نظرية النسبية العامة.
ثابت الجاذبية
إن تعيين قيمة هذا الثابت الأساسي من ثوابت الفيزياء بالتجربة عملية صعبة ومركبة. ومن العمليات التي اتُّبعت في هذا الشأن تجربة، كان كافنديش Cavendish أول من أجراها (عام 1798)، وتقضي هذه التجربة بقياس الدور الاهتزازي لنواس فتل يتألف من سلك دقيق جداً معلق شاقولياً ويحمل في نهايته السفلى قضيباً صلباً دقيقاً يعلق من منتصفه بالسلك، ويحمل في طرفيه كرتين صغيرتين (الشكل -1).
يقاس دور اهتزاز هذا النواس حول سلكه الشاقولي، وهو بعيد قدر الإمكان عن كل تأثير خارجي، ثم يوضع بالقرب من الكُرتين، وفي جهتي القضيب الأفقي، كرتان ثقيلتان كبيرتان مركزاهما في مستوي النوسان الأفقي. فتعاني كل كُريَّة قوةَ جذب ضعيفة إلى الكرة التي بقربها، ومن ثم تنشأ مزدوجة فتل إضافية، مما يؤدي إلى تغيّر دور نوسان القضيب الأفقي. ومن الفرق بين الدورين تُحسب مزدوجة القوى الإضافية، ثم قوة التجاذب بين كل كرية والكرة التي تقابلها. وبتطبيق قانون نيوتن في الجاذبية على هذه القوة تحسب قيمة الثابت ث.
إن أحسن قيمة مقبولة اليوم لهذا الثابت هي تلك التي قاسها الأمريكيان هيل P.R.Heyl وشرزانوفسكي P.Chrzanovski فوجدا:
إن الارتياب النسبي الكبير هنا لا يفي بالدقة التي يحتاج إليها الفلكيون في الميكانيك السماوي اليوم. والواقع أن الميكانيك السماوي يحتاج إلى الجداء
ثا = ث.ك، حيث ك كتلة الشمس، ويسمى ثابت الجاذبية المركزي الشمسي constante héliocentrique de la gravitation. ويحسب الفلكيون قيمته في جملة وحدات تلائمهم، فيعتمدون كتلة الشمس ك وحدةً للكتل، واليوم (86400 ثانية) وحدةً للزمن، ونصف القطر الكبير لمدار الأرض وحدةً للطول، فيكون:
ثا = 0.01720209895
أما في دراسة حركة القمر والأقمار الصنعية فيحتاجون إلى الثابت ثاَ = ث.كَ، حيث كَ كتلة الأرض. ولدى اعتماد هذه الكتلة وحدةً للكتل وجدوا، من دراسة حركة المسابير sondes القمرية، أن:
مبدأ التكافؤ Principe d’équivalence
إن أوزان الأجسام المادية من أكثر مظاهر الجاذبية شيوعاً في الممارسات اليومية، ومن أطوعها للقياس المباشر. وقوة الوزن تتألف من قوتين تنضمان معاً بالجمع المتجه (الشعاعي): قوة الجذب التثاقلية الناجمة عن كتلة الأرض والقوة النابذة الناجمة عن دوران الأرض. إن هاتين القوتين هما، في عرف ميكانيك نيوتن، من روحين مختلفتين جداً، فقوة الجذب التثاقلي تتناسب، بموجب قانون نيوتن، طرداً مع كتلة الجسم، ولذلك تسمى الكتلة المعرَّفة بهذا الشكل باسم الكتلة التثاقلية masse gravitationnelle. وسنرمز لها بـ ك.
أما القوة النابذة ق فتتناسب مع مربع سرعة الدوران الزاوية سه2، ومع بعد الجسم عن محور الدوران م أي:
حيث كَ عامل تناسب، وهو يسمى الكتلة العطالية masse inertielle للجسم.
ما من سبب يدعو إلى الاعتقاد بوجود علاقة بين الكتلة الثقالية والكتلة العطالية للجسم الواحد، لكن الواقع قد أظهر، منذ عصر نيوتن، أن بين هذين المقدارين تناسباً طردياً مباشراً. وقد بيَّن الفيزيائي المجري أُتفوس L.Eötvös بتجربة شهيرة أجراها عام 1909 أن قوة الوزن، بمركبتيها الثقالية والعطالية، مستقلة عن كتلة الجسم أو عن كثافته. وهذا يعني أن ك=كَ، لأن مركبتي الوزن تتصرفان بأسلوب واحد لدى تغيير كتلة الجسم الخاضع للتجربة.
إن هذا التساوي بين الكتلة الثقالية والكتلة العطالية كان يُعتبر في ميكانيك نيوتن مصادفة بحتة، لكن أينشتاين رأى فيه مغزى عميقاً، فاتخذه منطلقاً أساسيا ًاكتشف بفضله نظرية النسبية العامة. إنه خاصية يتميز بها حقل الجاذبية وحده، بخلاف الحقل الكهربائي والحقل المغنطيسي مثلاً، وهي تدل على أن الجاذبية في حقيقتها قوة عطالية وأن القوانين التي تحكمها تعبر عن عطالة المادة.
الجاذبية في النسبية العامة
لم يكن أينشتاين يستسيغ فكرة التفاعل عن بعد بين جسمين يفصل بينهما فضاء خالٍ، تلك الفكرة التي يقوم عليها قانون نيوتن في الجاذبية الثقالية. وقد توصل عام 1905 إلى نظريته النسبوية الخاصة التي من أهم سماتها أن ربطت بين المكان (المسافة) والزمان برباط وثيق جعل منهما معاً كائناً فيزيائياً واحداً يُعرف اليوم باسم الزمان ـ المكان (أو الزمكان اختصاراً) وبين المادة والطاقة برباط آخر من شأنه أن يتيح تحول المادة إلى طاقة والعكس.
وفي عام 1915 جاء أينشتاين بنظرية جديدة أخرى تعرف اليوم باسم النسبية العامة. توحي الصورة الرياضية (الرياضياتية) لمعادلات النسبية العامة بأن المادة، أو الطاقة، تؤثر في الزمكان تأثيراً من شأنه أن يجعل الزمكان «متوتراً» أو «منحنيا» كصورة توتر الخيط المطاطي في الفضاء ذي البعد الواحد أو كصورة انحناء السطوح في الفضاء ذي البعدين. وأن من شأن الزمكان أن يؤثر عندئذ بدوره في الأشياء المادية، كائناً فيزيائياً دينامياً (يتأثر بالمادة ويؤثر فيها)، لا كما كان، في ميكانيك نيوتن، مجرد مسرح خامل تقع فيه الأحداث.
ويأخذ التجاذب التثاقلي بين كتلتين ماديتين، في معادلات النسبية العامة، صورة فعل ناجم عن توتر زمكاني تولده الكتلتان في الفضاء المجاور لهما. ثم إن كتلة الشمس تولّد، في الفضاء حولها، زمكاناً منحنياً شبه منغلق بشكل إهليلجات تحيط بالشمس، ومن شأن الكواكب أن تتأثر في حركتها العطالية بهذا الانحناء الزمكاني فتسلك تلك المدارات الإهليلجية.
إن المسارات التي تسلكها الأجسام في الحقل التجاذبي تسمى في علم الرياضيات جيوديزيات géodésiques الفضاء الزمكاني (جيوديزي في فضاء ما هو عموماً أقصر مسافة بين نقطتين من ذلك الفضاء، فهو في السطح المستوي، مثلاً، خط مستقيم بينهما، وعلى سطح الكرة هو قوس الدائرة العظمى بينهما). ومعلوم في النسبية العامة أن الحصول على مسار جسم ما يستدعي حساب جيوديزيات معادلات رياضية تفاضلية من الشكل:
حيث يمثل تفا ل عنصر الطول من الخط الجيوديزي، ويشير الدليلان ن و هـ بحسب قيمهما (من 1 إلى 4)، إلى إحداثيات الزمكان الأربعة (ثلاثة مكانية، س، ع، ص، وواحد زمني ز). أما المضاريب جن هـ فتتعلق بتوزع الكتل وبحركة مرجع المقارنة، وتتخذ في النسبية العامة شكلاً مختلفاً جداً عن شكلها في ميكانيك نيوتن؛ وهنا يكمن الفرق الجوهري بين النظريتين.
يقود حل هذه المعادلات إلى مسارات مجاورة جداً للمسارات التي يعطيها قانون نيوتن، مع فروق محسوسة في جوار كتل كبيرة جداً. وهذا شأن الكوكب عطارد الخفيف والقريب جداً من الشمس؛ وهنا يتجلى الفرق بحركة دائرية بطيئة يقوم بها أوج مدار الكوكب سرعتُها 43 ثانية قوسية في القرن الواحد؛ أي إن إهليلج المدار غير مغلق تماماً، وهي قيمة تتفق جيداً مع القياسات الرصدية. وهذا المفعول أضعف بكثير في حال الزهرة والأرض بسبب بعديهما الكبيرين عن الشمس، فضلاً عن الكواكب الأخرى التي هي أبعد بكثير عن الشمس.
هذا ومن الجدير أن نلاحظ أن تَعَلُّق تفا ل2 بالكتل وبحركة المرجع معاً يضمن الاستجابة لمبدأ التكافؤ بين المفعولين، الثقالي والعطالي، في الجسم الواحد.
ثم إن من المهم جداً أن يُشار إلى أن الشكل التفاضلي للمعادلة السابقة يدل على أن النسبية العامة هي في الواقع نظرية موضعية locale في الجاذبية، ومن روح هندسية صرفة (تشوه الفضاء الزمكاني)، وقد يحسن أن لا تُستعمل بصددها كلمة «الجاذبية».
الموجات التجاذبية
على شاكلة الموجات الكهرطيسية التي تصدر عن شحنات كهربائية متحركة، تتنبأ معادلات النسبية العامة بأن الكتل المادية المتحركة تفقد قسطاً من طاقتها تحمله موجات تسمى الموجات التجاذبية وتنتشر بسرعة الضوء. وهذه الأمواج، عندما تخترق جملة مادية، تولد اهتزازات عرضانية للمسافات الفاصلة بين الأجسام المادية. ولئن تعذر كشفها حتى الآن في تجارب أرضية، بسبب ضعف سعتها الشديد، فقد تأكد وجودها عن طريق غير مباشر بوساطة عمليات رصد اضطراب حركة بعض النَّبَّاضات الثنائية pulsars binaires.
وهناك اليوم عدة مشروعات في طور التنفيذ تهدف إلى استكشاف أمواج تجاذبية صادرة عن حركات أجرام سماوية كبيرة، كالمجرات، أو عن تفجرها. وفي عام 1958 صُنع كاشف لهذه الموجات يتألف من أسطوانات تهتز بفعل الموجات التجاذبية الآتية من تلك الأجرام اهتزازاً قد لا تتجاوز سعته قطر الذرة، ويُكشف بجهاز تداخل ليزريّ دقيق جداً. وللتيقن من سبب هذا الاهتزاز تُستخدم عدة كواشف متماثلة قد تبلغ المسافات فيما بينها ألف كيلو متر، فتهتز أسطواناتها في وقت واحد وسعة واحدة، إذا كان سببها موجات تجاذبية آتية من خارج الكرة الأرضية. ولئن تم اكتشاف عددٍ لا بأس به من ظواهر ذات ملامح قوية من هذا القبيل، إلا أن هذا الأمر لا يزال بحاجة إلى مزيد من الأرصاد في المشروعات التي تم تنفيذ بعضها وما يزال بعضها الآخر في مرحلة التنفيذ.
أدهم السمان
Gravitation - Gravitation
الجاذبية
الجاذبية gravitation خاصية من خصائص المادة (والطاقة، بموجب نظرية النسبية) تتجلى بقوة تجاذبٍ يحدث فيما بين أجزائها، مهما كانت صغيرة أو كبيرة ومهما كانت المسافات الفاصلة فيما بينها، فهي إذن قوة واسعة الشمول.
قانون نيوتن العام في الجاذبية
يرى نيوتن أن هذا التجاذب بين نقطتين ماديتين، كتلتاهما ك1 وك2، نابع من قوة ق، تتناسب طردياً مع كل من الكتلتين وعكساً مع م2، ومحمولة على المستقيم الواصل بينهما أي إن الكتلة النقطية ك1 تخضع، من جراء وجود الكتلة النقطية ك2 ع
 لى المسافة م منها، لـ قوة ق تستجيب للعلاقة:
لى المسافة م منها، لـ قوة ق تستجيب للعلاقة: |
 |
متجهة طولها يساوي وحدة الطول، وتذهب من الكتلة المنفعلة ك1 إلى الكتلة الفاعلة ك2. وحيث ث مقدار يسمى ثابت الجاذبية العام ويجري تعيينه بالتجربة. |
إن قوة التجاذب هذه تخضع لمبدأ تساوي الفعل ورد الفعل؛ أي إن الكتلة ك2 تخضع، في الشروط نفسها، إلى قوةٍ تساوي  . . |
حظي قانون نيوتن هذا بشواهد تجريبية ذات دقة عالية؛ وقد يكون أهمها ما تبين من أنه يفسر تفسيراً جيداً قوانين كبلر Kepler في الميكانيك السماوي، فهو يتيح مثلاً، تعيين مواقع الكواكب في المنظومة الشمسية بفرق ٍبين الموقع المقيس والموقع المحسوب بوساطته وباستخدام قوانين نيوتن التحريكية، لا يزيد على عُشر ثانية قوسية وعلى مدى عشرات الدورات الكوكبية أو مئاتها، ولم يشذ عن هذا القانون سوى عطارد، وبمقدار أقل الزُّهرة والأرض (وهي كواكب خفيفة أقرب إلى الشمس، وقد أمكن تفسير هذا الشذوذ الضعيف في إطار نظرية النسبية العامة، كما سيُرى بعد قليل).
ثمة شاهد إضافي على عمومية هذا القانون في علم الفلك وهو «الحركة النسبية للنجوم الثنائية» étoiles doubles إذ يدور كل نجم حول رفيقه وفق إهليلج (قطع ناقص) يستجيب لقوانين كبلر، وهي نتيجة لقوانين نيوتن، وهنا أيضاً تشذ عن هذا القانون الثنائية العظيمة الكتلة شذوذاً تفسره نظرية النسبية العامة.
ثابت الجاذبية
إن تعيين قيمة هذا الثابت الأساسي من ثوابت الفيزياء بالتجربة عملية صعبة ومركبة. ومن العمليات التي اتُّبعت في هذا الشأن تجربة، كان كافنديش Cavendish أول من أجراها (عام 1798)، وتقضي هذه التجربة بقياس الدور الاهتزازي لنواس فتل يتألف من سلك دقيق جداً معلق شاقولياً ويحمل في نهايته السفلى قضيباً صلباً دقيقاً يعلق من منتصفه بالسلك، ويحمل في طرفيه كرتين صغيرتين (الشكل -1).
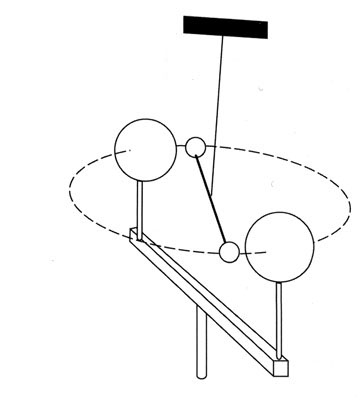 الشكل (1) مخطط تجربة كافنديش لقياس ثابت التثاقل |
إن أحسن قيمة مقبولة اليوم لهذا الثابت هي تلك التي قاسها الأمريكيان هيل P.R.Heyl وشرزانوفسكي P.Chrzanovski فوجدا:
 |
ثا = ث.ك، حيث ك كتلة الشمس، ويسمى ثابت الجاذبية المركزي الشمسي constante héliocentrique de la gravitation. ويحسب الفلكيون قيمته في جملة وحدات تلائمهم، فيعتمدون كتلة الشمس ك وحدةً للكتل، واليوم (86400 ثانية) وحدةً للزمن، ونصف القطر الكبير لمدار الأرض وحدةً للطول، فيكون:
ثا = 0.01720209895
أما في دراسة حركة القمر والأقمار الصنعية فيحتاجون إلى الثابت ثاَ = ث.كَ، حيث كَ كتلة الأرض. ولدى اعتماد هذه الكتلة وحدةً للكتل وجدوا، من دراسة حركة المسابير sondes القمرية، أن:
 |
إن أوزان الأجسام المادية من أكثر مظاهر الجاذبية شيوعاً في الممارسات اليومية، ومن أطوعها للقياس المباشر. وقوة الوزن تتألف من قوتين تنضمان معاً بالجمع المتجه (الشعاعي): قوة الجذب التثاقلية الناجمة عن كتلة الأرض والقوة النابذة الناجمة عن دوران الأرض. إن هاتين القوتين هما، في عرف ميكانيك نيوتن، من روحين مختلفتين جداً، فقوة الجذب التثاقلي تتناسب، بموجب قانون نيوتن، طرداً مع كتلة الجسم، ولذلك تسمى الكتلة المعرَّفة بهذا الشكل باسم الكتلة التثاقلية masse gravitationnelle. وسنرمز لها بـ ك.
أما القوة النابذة ق فتتناسب مع مربع سرعة الدوران الزاوية سه2، ومع بعد الجسم عن محور الدوران م أي:
 |
ما من سبب يدعو إلى الاعتقاد بوجود علاقة بين الكتلة الثقالية والكتلة العطالية للجسم الواحد، لكن الواقع قد أظهر، منذ عصر نيوتن، أن بين هذين المقدارين تناسباً طردياً مباشراً. وقد بيَّن الفيزيائي المجري أُتفوس L.Eötvös بتجربة شهيرة أجراها عام 1909 أن قوة الوزن، بمركبتيها الثقالية والعطالية، مستقلة عن كتلة الجسم أو عن كثافته. وهذا يعني أن ك=كَ، لأن مركبتي الوزن تتصرفان بأسلوب واحد لدى تغيير كتلة الجسم الخاضع للتجربة.
إن هذا التساوي بين الكتلة الثقالية والكتلة العطالية كان يُعتبر في ميكانيك نيوتن مصادفة بحتة، لكن أينشتاين رأى فيه مغزى عميقاً، فاتخذه منطلقاً أساسيا ًاكتشف بفضله نظرية النسبية العامة. إنه خاصية يتميز بها حقل الجاذبية وحده، بخلاف الحقل الكهربائي والحقل المغنطيسي مثلاً، وهي تدل على أن الجاذبية في حقيقتها قوة عطالية وأن القوانين التي تحكمها تعبر عن عطالة المادة.
الجاذبية في النسبية العامة
لم يكن أينشتاين يستسيغ فكرة التفاعل عن بعد بين جسمين يفصل بينهما فضاء خالٍ، تلك الفكرة التي يقوم عليها قانون نيوتن في الجاذبية الثقالية. وقد توصل عام 1905 إلى نظريته النسبوية الخاصة التي من أهم سماتها أن ربطت بين المكان (المسافة) والزمان برباط وثيق جعل منهما معاً كائناً فيزيائياً واحداً يُعرف اليوم باسم الزمان ـ المكان (أو الزمكان اختصاراً) وبين المادة والطاقة برباط آخر من شأنه أن يتيح تحول المادة إلى طاقة والعكس.
وفي عام 1915 جاء أينشتاين بنظرية جديدة أخرى تعرف اليوم باسم النسبية العامة. توحي الصورة الرياضية (الرياضياتية) لمعادلات النسبية العامة بأن المادة، أو الطاقة، تؤثر في الزمكان تأثيراً من شأنه أن يجعل الزمكان «متوتراً» أو «منحنيا» كصورة توتر الخيط المطاطي في الفضاء ذي البعد الواحد أو كصورة انحناء السطوح في الفضاء ذي البعدين. وأن من شأن الزمكان أن يؤثر عندئذ بدوره في الأشياء المادية، كائناً فيزيائياً دينامياً (يتأثر بالمادة ويؤثر فيها)، لا كما كان، في ميكانيك نيوتن، مجرد مسرح خامل تقع فيه الأحداث.
ويأخذ التجاذب التثاقلي بين كتلتين ماديتين، في معادلات النسبية العامة، صورة فعل ناجم عن توتر زمكاني تولده الكتلتان في الفضاء المجاور لهما. ثم إن كتلة الشمس تولّد، في الفضاء حولها، زمكاناً منحنياً شبه منغلق بشكل إهليلجات تحيط بالشمس، ومن شأن الكواكب أن تتأثر في حركتها العطالية بهذا الانحناء الزمكاني فتسلك تلك المدارات الإهليلجية.
إن المسارات التي تسلكها الأجسام في الحقل التجاذبي تسمى في علم الرياضيات جيوديزيات géodésiques الفضاء الزمكاني (جيوديزي في فضاء ما هو عموماً أقصر مسافة بين نقطتين من ذلك الفضاء، فهو في السطح المستوي، مثلاً، خط مستقيم بينهما، وعلى سطح الكرة هو قوس الدائرة العظمى بينهما). ومعلوم في النسبية العامة أن الحصول على مسار جسم ما يستدعي حساب جيوديزيات معادلات رياضية تفاضلية من الشكل:
 |
يقود حل هذه المعادلات إلى مسارات مجاورة جداً للمسارات التي يعطيها قانون نيوتن، مع فروق محسوسة في جوار كتل كبيرة جداً. وهذا شأن الكوكب عطارد الخفيف والقريب جداً من الشمس؛ وهنا يتجلى الفرق بحركة دائرية بطيئة يقوم بها أوج مدار الكوكب سرعتُها 43 ثانية قوسية في القرن الواحد؛ أي إن إهليلج المدار غير مغلق تماماً، وهي قيمة تتفق جيداً مع القياسات الرصدية. وهذا المفعول أضعف بكثير في حال الزهرة والأرض بسبب بعديهما الكبيرين عن الشمس، فضلاً عن الكواكب الأخرى التي هي أبعد بكثير عن الشمس.
هذا ومن الجدير أن نلاحظ أن تَعَلُّق تفا ل2 بالكتل وبحركة المرجع معاً يضمن الاستجابة لمبدأ التكافؤ بين المفعولين، الثقالي والعطالي، في الجسم الواحد.
ثم إن من المهم جداً أن يُشار إلى أن الشكل التفاضلي للمعادلة السابقة يدل على أن النسبية العامة هي في الواقع نظرية موضعية locale في الجاذبية، ومن روح هندسية صرفة (تشوه الفضاء الزمكاني)، وقد يحسن أن لا تُستعمل بصددها كلمة «الجاذبية».
الموجات التجاذبية
على شاكلة الموجات الكهرطيسية التي تصدر عن شحنات كهربائية متحركة، تتنبأ معادلات النسبية العامة بأن الكتل المادية المتحركة تفقد قسطاً من طاقتها تحمله موجات تسمى الموجات التجاذبية وتنتشر بسرعة الضوء. وهذه الأمواج، عندما تخترق جملة مادية، تولد اهتزازات عرضانية للمسافات الفاصلة بين الأجسام المادية. ولئن تعذر كشفها حتى الآن في تجارب أرضية، بسبب ضعف سعتها الشديد، فقد تأكد وجودها عن طريق غير مباشر بوساطة عمليات رصد اضطراب حركة بعض النَّبَّاضات الثنائية pulsars binaires.
وهناك اليوم عدة مشروعات في طور التنفيذ تهدف إلى استكشاف أمواج تجاذبية صادرة عن حركات أجرام سماوية كبيرة، كالمجرات، أو عن تفجرها. وفي عام 1958 صُنع كاشف لهذه الموجات يتألف من أسطوانات تهتز بفعل الموجات التجاذبية الآتية من تلك الأجرام اهتزازاً قد لا تتجاوز سعته قطر الذرة، ويُكشف بجهاز تداخل ليزريّ دقيق جداً. وللتيقن من سبب هذا الاهتزاز تُستخدم عدة كواشف متماثلة قد تبلغ المسافات فيما بينها ألف كيلو متر، فتهتز أسطواناتها في وقت واحد وسعة واحدة، إذا كان سببها موجات تجاذبية آتية من خارج الكرة الأرضية. ولئن تم اكتشاف عددٍ لا بأس به من ظواهر ذات ملامح قوية من هذا القبيل، إلا أن هذا الأمر لا يزال بحاجة إلى مزيد من الأرصاد في المشروعات التي تم تنفيذ بعضها وما يزال بعضها الآخر في مرحلة التنفيذ.
أدهم السمان
