
العدد النيبيري وكيفية حسابه واستخداماته
حسام سليمان
تم التدقيق بواسطة: فريق أراجيك
العدد النيبيري
حساب e
استخدمات العدد النيبيري
أهمية العدد النيبيري
العدد النيبيري عبارة عن رقمٍ موجودٍ في الرياضيات، ولكن ليس كأي رقمٍ عاديٍّ، فقد قِيلَ أنه يعادل سوناتات شكسبير، كما وُصِف بأنه من أجمل المعادلات في الرياضيات، ووصفه الفيزيائي الكبير الراحل ريتشارد فاينمان في محاضراته بأنه "جوهر الدينا" و "المعادلة الأكثر بروزًا في الرياضيات"، يوجد العديد من المجالات المثيرة للاهتمام لهذا العدد، لذا يستحق أخذ أفكار عامة حوله.
العدد النيبيري
الثابت "e" أو كما نعرفه بالعدد النيبيري، هو رقمٌ حقيقيٌّ غير نسبيٍّ (أي أن منازله بعد الفاصلة لا تتكرر ولا تنتهي)، و ليس كسريًّا (لا يمكن كتابته ككسر)، يعد أساس اللوغاريتم الطبيعي، ويعتبره البعض أهم الثوابت الرياضيّة المُكتشفة، والذي قدم لنا تسهيلاتٍ بكتابة المعادلات الرياضية (كالتفاضل والتكامل).
يستمر الامتداد العشري للعدد النيبيري إلى اللانهاية بدون أي تكرارٍ في الأرقام، كما أن هذا الرقم هو متسامٍ، مما يعني أنه ليس جذرًا لأية معادلةٍ كثيرة الحدود ذات أمثالٍ صحيحةٍ، يُطلق عليه أحيانًا أيضًا رقم أويلر؛ نسبةً إلى عالم الرياضيات السويسري ليونهارت أويلر (1707-1783)، أما تسميته "العدد النيبيري" فكانت نسبةً إلى عالم الرياضيات الاسكتلندي جون نابير (1550-1617).
يعد العدد النيبيري الثابت الأكثر أهمية في الرياضيات لأنه يظهر في سياقاتٍ رياضيةٍ لا تعد ولا تحصى، تتضمن حدودًا ومشتقاتٍ عدة، يتفرّد هذا الرقم بخاصيةٍ محددةٍ بمنطقةٍ محددةٍ بمساحة القطع الزائد (y=1/x)، والمحور (x) و الخطوط العامودية (x=1 وx=e)، أو بمعنى آخر:
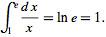
كان هذا العدد محط اهتمام علماء الرياضيات على مرِّ العصور، وشغل جزءًا كبيرًا من أبحاثهم، أثبت أويلر أنه عددٌ لا كسري من خلال عمليةٍ كسريةٍ بسيطة مستمرة ولا نهائية، كما برهن العالم جوزيف ليوفيل في عام 1844، بأن أي معادلةٍ من الدرجة الثانية لا تفي بالغرض عند استخدامها مع معادلاتٍ تربيعيةٍ ذات معاملاتٍ تكامليةٍ (أي إذا كانت المعادلة جبرية، فيجب أن تكون جبريةً بدرجةٍ أكبر من 2)، ثُمَّ قام العالم شارل آرميت في عام 1873 بعد ذلك بحل المشكلة، حيث أثبت أن العدد e غير جبري. 1 .
حساب e
هناك العديد من الطرق لحساب قيمة e، لكن أيًا منها للأسف لم يقدم إجابةً دقيقةً تمامًا، كونه عدد لا كسري وأرقامه تستمر إلى الأبد ودون تكرار، ولكن المعروف أنه يوجد أكثر من تريليون رقم.
يمكننا حساب قيمة e من خلال العلاقة [1+(1/n[(n، فكلما زادت قيمة n اقتربنا من قيمة e وهكذا.
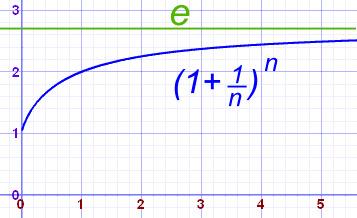
طريقة آخرى:
يعد أويلر أول من استطاع الوصول نسبيًّا لقيمة العدد النيبيري e، عن طريق مجموع الكسور اللامتناهية هذه:
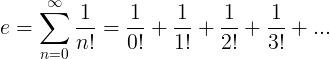
فإذا عوضنا بالعلاقة السابقة، سنصل تقريبًا (كما فعل أويلر) إلى 18 منزلةً عشريةً، وذلك من خلال تعويضنا فيما سبق والحل:
...2.718055556 =.....1/120 + 1/24 + 1/6 + 1/2 + 1 + 1
وإذا تابعنا التعويض من خلال تلك العلاقة سنصل لقيمة e: 2 .

استخدمات العدد النيبيري
- العدد e يعد أساس اللوغاريتم الطبيعي، فمنذ أن اخترع نابير اللوغاريتم، يشار إلى العدد e باسم العدد النيبيري أو ثابت نايبر.
- له دورٌ أساسيٌّ في حساب التفاضل والتكامل، فالدالة الأسيّة ex لها خاصية فريدة من نوعها كونها مُشتقة بحد ذاتها.
- تتحد التعبيرات التي تتضمن ex وe-x أي (ex =cosh x + sinh x و eix = cos x + isin x) لتشكيل دالة الجيب والتجيب الزائديّة.
- بفضل اكتشاف أويلر العدد النيبيري، بتنا نعلم أن الثوابت الأساسية للرياضيات مرتبطة ببعضها بالصيغة eiΠ +1=0 (حيث i عدد تخيّلي والذي هو الجذر التربيعي للـ 1-).
- يظهر الرقم e في صيغ مختلفة في جميع مجالات الرياضيات، وخاصة في مجال نظرية الأعداد. 3 .
إن العدد النيبيري ذو أهميةٍ خاصةٍ، حيث يلعب أدوارً أساسيةً في الرياضيات ويشكل إلى جانب (0،1،i،π)، ما يسمى الثوابت الخمسة، التي تظهر في صياغة متطابقة أويلر، وتنص بأن أي ثابتٍ هو عددٌ غير نسبيٍّ (لا يُكتب كنسبةٍ من الأعداد الصحيحة)، وغير جبريٍّ (أي ليس جذر لأي كثير حدود غير صفرية في الأعداد جذرية).
أحد أكثر المواضيع أهمية بخصوص العدد النيبيري هو صيغة الفائدة المُركبة، والتي اكتشفها العالم ياكوب بيرنولي، من خلال طرح أسئلة تتعلق بفوائد مبالغ الأموال في حساباتٍ معينةٍ، خلال عدد معين من السنوات.
وصل بيرنولي في النهاية إلى علاقةٍ نستطيع من خلالها الوصول إلى قيمة الفائدة المركبة، فإذا كانت الفائدة تتضاعف لعدد n مرة في السنة، و لدينا صيغة مفادها أنه إذا كان معدل الفائدة هو r في المائة، مع المبلغ المقدر ب P دولار، فسوف نصل للمبلغ بعد t سنوات عن طريق المعادلة الآتية: A=P(1+r/n)nt.
عند سؤاله عما يحدث عندما تزداد عدد الفترات n بشكلٍ عشوائيٍّ، كان قادرًا على الخروج بصيغة الفائدة المركبة المستمرة، وهي A=Pert. 4 .
المصادر
