تويت
وتر مهتز
Vibrating string - Corde vibrante
الوتر المهتز
ينشأ الاهتزاز vibration في وتر string مرن ومشدود ومثبت من إحدى نهايتيه أو كلتيهما نتيجة اضطراب طولاني أو عرضاني يَحدث فيه فيخرجه عن وضع توازنه. ينتشر هذا الاضطراب عبر الوتر مع الزمن على شكل موجة [ر]، وتخضع الجسيمات المكونة له لانزياحات مختلفة تحددها طبيعة الموجة.
تعطى سرعة انتشار موجة الاضطراب ـ وهي تتعلق بالخصائص الميكانيكية للوتر فقط ـ بالعلاقة:
حيث T هي التوتر (قوة الشد) المطبق على الوتر، و μ كتلة واحدة الطول منه. فإذا كانت كتلته m وطوله L فإن
μ = m/L.
إذا أُحدث اضطراب طولاني أو عرضاني عند إحدى نهايتي الوتر، لتكن النهاية الواقعة عند x = 0، وكان على شكل موجة جيبية سعتها A وتواترها الزاوي ω = 2π f حيث f التواتر معطاة بالعلاقة:
(2) y (x = 0, t) = A sin ωt
حيث t الزمن و y الانزياح فإن هذا الاضطراب ينتشر في الوتر ويصل إلى نقطة منه تبعد مسافة x عن المبدأ بعد زمن قدره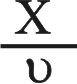
، وتعطى معادلة انزياح هذه النقطة في اللحظة t بالعلاقة:
(3) y (x, t) = A sin (ω t ± κ x)
حيث تدل إشارة (-) إلى انتقال نحو اليمين، وإشارة (+) إلى انتقال نحو اليسار. أما الثابتة k فهي العدد الموجي wave number وتساوي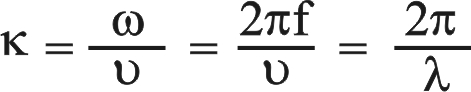
حيث λ طول موجة الاهتزاز. وتجدر الإشارة هنا إلى أن الذي ينتقل بتلك السرعة هو الاضطراب أما جزيئات الوتر فتتحرك في مواضعها للأعلى وللأسفل أو ذهاباً وإياباً. وتعطي المعادلة (3) تغير الانزياح y لنقطة معينة x من الوتر بدلالة الزمن، أو التغير في لحظة معينة t لأي نقطة من الوتر.
الأمواج المستقرة في وتر مشدود مثبت من نهايتيه
عندما تصل الموجة إلى نقطة تثبيت الوتر في نهايته تنعكس هناك وترجع منتشرة على الوتر بالاتجاه المعاكس. ففي كل نقطة من الوتر تبعد مسافة x عن المبدأ تؤثر موجتان، موجة منتقلة نحو نقطة الربط وموجة منعكسة عندها، فتتراكب الموجتان وتتداخلان وتنشأ موجة مستقرة ويصبح الوتر على شكل المغزل (أو المغازل).
توجد على الوتر نقاط تنعدم فيها الحركة تسمى العُقَد nodes كما توجد بين العُقَد نقاط تكون سعة الحركة فيها أعظمية تسمى البطون antinodes (الشكل 1).
ولاشتقاق صيغة دالة الموجة المستقرة تجمع الدالتان y1(x, t) و y2(x, t) للموجتين اللتين لهما سعة واحدة ودور واحد وطول موجي واحد وتنتشران في اتجاهين متعاكسين، وممثلتان بالمعادلة (3). فالمعادلة y1(x, t) = A sin (ωt + κx) تمثل موجة واردة تنتقل إلى اليسار على المحور x+، وعندما تصل إلى النقطة x تساوي الصفر تنعكس. والمعادلة y2(x, t) = -A sin (ωt – κx) تمثل موجة منعكسة تنتشر إلى يمين النقطة x = الصفر. والدالة y (t, x) هي حاصل جمع الدالتين:
(4) y (x, t) = y1(x, t) + y2(x, t) = (2A sin κx) cos ωt
وهي معادلة موجة مستقرة في وتر مثبت عند الطرف x = الصفر. تحدث العقد من أجل sin κx = 0، ويحدث هذا من أجل κx = 0, π, 2π, 3π,....
ولما كان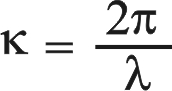
فإن مواضع العقد الممكنة هي:
أو بدلالة λ:
ويُبَيّن الشكل (2) تشكل الموجات المستقرة من أجل قيم n المساوية 1 و 2 و 3 و 4.
التواتر الأساسي والتوافقيات والأنماط
عند نقر وتر طوله محدد L ومثبت من نهايتيه بإحكام ـ شأن الأوتار في معظم الآلات الموسيقية الوترية ـ تنتج موجة مستقرة. تولِّد هذه الموجةُ المستقرة موجةً صوتية في الهواء تواترها هو تواتر تجاوب الوتر، الذي يتعين بخواص الوتر. ينبغي أن يكون للموجة المستقرة التي تنشأ في الوتر عقدتان في طرفيه المثبتين. وهذا ما يحدّ من الاهتزازات المحتملة. فطول الموجة يجب أن يكون مساوياً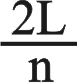
، وهذا يوافق من أجل n =1 صوتاً صادراً عن الوتر تواتره 
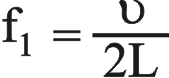، وهو ما يعرف بالتواتر الأساسي fundamental frequency (الشكل 2) حيث تتشكل عقدة عند كل من الطرفين وبطن في المنتصف. يمثل هذا واحداً من أنماط اهتزاز الوتر، وبالرجوع إلى المعادلة (1) يعطى التواتر الأساسي بالعلاقة:
يهتز الوتر المثالي بالتواتر الأساسي ومضاعفاته التي تدعى كل التوافقيات التابعة لذلك التواتر. وتكون مواضع العقد والبطون معاكسة لمثيلاتها التي تحدث في عمود الهواء المفتوح [ر. المزمار]. وتشير المعادلة (5) التي تعطي مواضع تشكل العقد في الوتر إلى أنه توجد أنماط أخرى مسموح بها.
ويبين الشكل (3) أمواجاً مستقرة عديدة تدعى التوافقيات harmonics (المدروجات) وهي الموافقة لقيم الأطوال الموجية التي يمكن الحصول عليها على الوتر المثبت من طرفيه، وهي:
ومنها تستنتج تواترات كل التوافقيات الخاصة بالوتر وهي:
طبقة الصوت
تتحدد طبقة الصوت الذي يصدره وتر مهتز بتواتر تجاوبه الذي يتعين بطوله وكتلته وبقوة الشد. كما تشير إلى ذلك المعادلتان (6) و (8). تتغير الطبقة بطرق مختلفة مع هذه الوسطاء المختلفة كما هو موضح في الأمثلة الآتية: إذا كان الوتر يبدأ بطبقة تواترها = 100 هرتز فمضاعفة الطول تخفِّض الطبقة إلى النصف، أي تجعلها 50 هرتز. وإذا تضاعفت قوة الشد أربع مرات فتصبح الطبقة 200 هرتز. أما إذا تضاعفت كتلته (مع بقاء طوله ثابتاً) فسيكون تواتره 50 هرتز. وهكذا فإن زيادة التواتر بمقدار ثُمانية واحدة (أي أوكتاف واحد) يتطلب مضاعفة قوة الشد أربع مرات. فمن أجل قوة شد To مطبقة على وتر معروف الطول والكتلة، يصدر صوتاً تواتره fo.
ويلخص الجدول (1) قوى الشد اللازمة لرفع طبقة الوتر بمقدار ثمانية واحدة (أوكتاف واحد) أو أكثر فوق f0.
محمد قعقع
Vibrating string - Corde vibrante
الوتر المهتز
ينشأ الاهتزاز vibration في وتر string مرن ومشدود ومثبت من إحدى نهايتيه أو كلتيهما نتيجة اضطراب طولاني أو عرضاني يَحدث فيه فيخرجه عن وضع توازنه. ينتشر هذا الاضطراب عبر الوتر مع الزمن على شكل موجة [ر]، وتخضع الجسيمات المكونة له لانزياحات مختلفة تحددها طبيعة الموجة.
تعطى سرعة انتشار موجة الاضطراب ـ وهي تتعلق بالخصائص الميكانيكية للوتر فقط ـ بالعلاقة:
 |
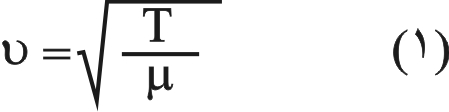μ = m/L.
إذا أُحدث اضطراب طولاني أو عرضاني عند إحدى نهايتي الوتر، لتكن النهاية الواقعة عند x = 0، وكان على شكل موجة جيبية سعتها A وتواترها الزاوي ω = 2π f حيث f التواتر معطاة بالعلاقة:
(2) y (x = 0, t) = A sin ωt
حيث t الزمن و y الانزياح فإن هذا الاضطراب ينتشر في الوتر ويصل إلى نقطة منه تبعد مسافة x عن المبدأ بعد زمن قدره
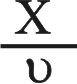، وتعطى معادلة انزياح هذه النقطة في اللحظة t بالعلاقة:(3) y (x, t) = A sin (ω t ± κ x)
حيث تدل إشارة (-) إلى انتقال نحو اليمين، وإشارة (+) إلى انتقال نحو اليسار. أما الثابتة k فهي العدد الموجي wave number وتساوي
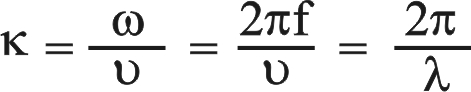حيث λ طول موجة الاهتزاز. وتجدر الإشارة هنا إلى أن الذي ينتقل بتلك السرعة هو الاضطراب أما جزيئات الوتر فتتحرك في مواضعها للأعلى وللأسفل أو ذهاباً وإياباً. وتعطي المعادلة (3) تغير الانزياح y لنقطة معينة x من الوتر بدلالة الزمن، أو التغير في لحظة معينة t لأي نقطة من الوتر.الأمواج المستقرة في وتر مشدود مثبت من نهايتيه
 |
| الشكل (1) تشكل العقد والبطون |
توجد على الوتر نقاط تنعدم فيها الحركة تسمى العُقَد nodes كما توجد بين العُقَد نقاط تكون سعة الحركة فيها أعظمية تسمى البطون antinodes (الشكل 1).
ولاشتقاق صيغة دالة الموجة المستقرة تجمع الدالتان y1(x, t) و y2(x, t) للموجتين اللتين لهما سعة واحدة ودور واحد وطول موجي واحد وتنتشران في اتجاهين متعاكسين، وممثلتان بالمعادلة (3). فالمعادلة y1(x, t) = A sin (ωt + κx) تمثل موجة واردة تنتقل إلى اليسار على المحور x+، وعندما تصل إلى النقطة x تساوي الصفر تنعكس. والمعادلة y2(x, t) = -A sin (ωt – κx) تمثل موجة منعكسة تنتشر إلى يمين النقطة x = الصفر. والدالة y (t, x) هي حاصل جمع الدالتين:
(4) y (x, t) = y1(x, t) + y2(x, t) = (2A sin κx) cos ωt
وهي معادلة موجة مستقرة في وتر مثبت عند الطرف x = الصفر. تحدث العقد من أجل sin κx = 0، ويحدث هذا من أجل κx = 0, π, 2π, 3π,....
ولما كان
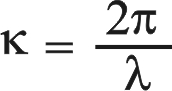فإن مواضع العقد الممكنة هي:  |
 |
 |
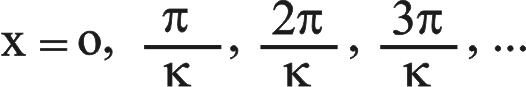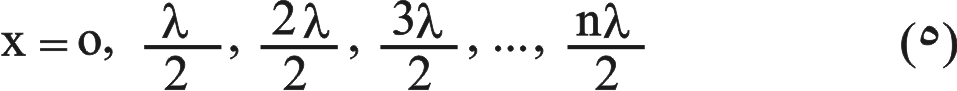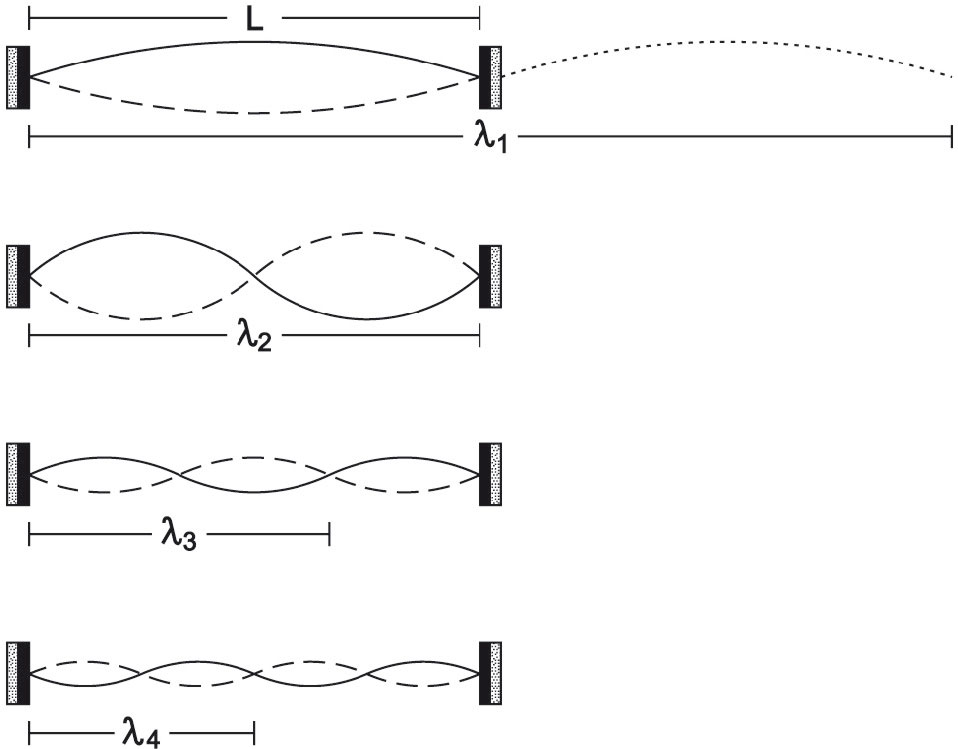| الشكل (2) تشكل الأمواج المستقرة الموافقة لأربعة أطوال موجية ممكنة |
التواتر الأساسي والتوافقيات والأنماط
عند نقر وتر طوله محدد L ومثبت من نهايتيه بإحكام ـ شأن الأوتار في معظم الآلات الموسيقية الوترية ـ تنتج موجة مستقرة. تولِّد هذه الموجةُ المستقرة موجةً صوتية في الهواء تواترها هو تواتر تجاوب الوتر، الذي يتعين بخواص الوتر. ينبغي أن يكون للموجة المستقرة التي تنشأ في الوتر عقدتان في طرفيه المثبتين. وهذا ما يحدّ من الاهتزازات المحتملة. فطول الموجة يجب أن يكون مساوياً
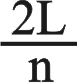، وهذا يوافق من أجل n =1 صوتاً صادراً عن الوتر تواتره 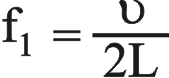، وهو ما يعرف بالتواتر الأساسي fundamental frequency (الشكل 2) حيث تتشكل عقدة عند كل من الطرفين وبطن في المنتصف. يمثل هذا واحداً من أنماط اهتزاز الوتر، وبالرجوع إلى المعادلة (1) يعطى التواتر الأساسي بالعلاقة:  |
 |
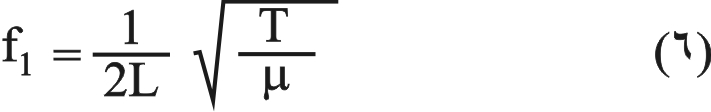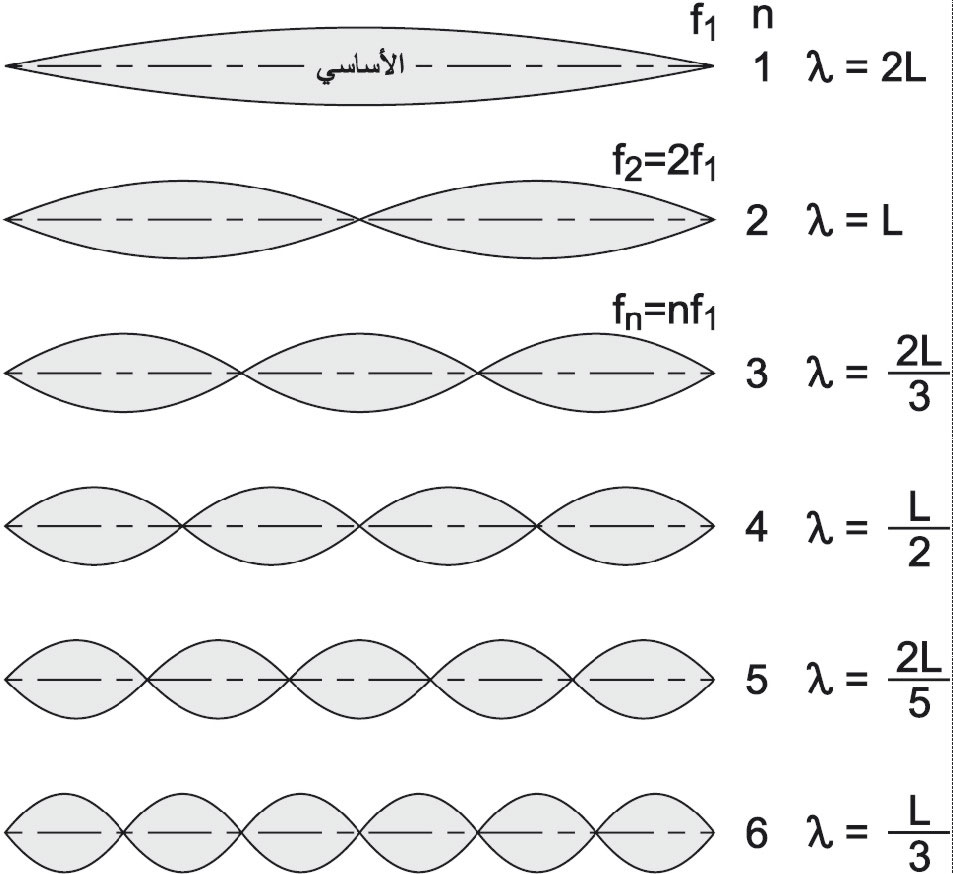| الشكل (3) التواتر الأساسي وتواترات التوافقيات الست الأولى لوتر مثبت من طرفيه |
 |
 |
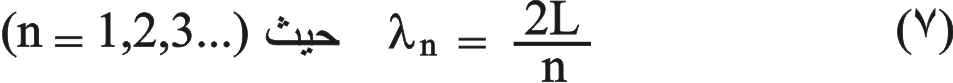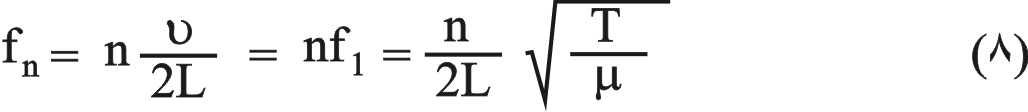تتحدد طبقة الصوت الذي يصدره وتر مهتز بتواتر تجاوبه الذي يتعين بطوله وكتلته وبقوة الشد. كما تشير إلى ذلك المعادلتان (6) و (8). تتغير الطبقة بطرق مختلفة مع هذه الوسطاء المختلفة كما هو موضح في الأمثلة الآتية: إذا كان الوتر يبدأ بطبقة تواترها = 100 هرتز فمضاعفة الطول تخفِّض الطبقة إلى النصف، أي تجعلها 50 هرتز. وإذا تضاعفت قوة الشد أربع مرات فتصبح الطبقة 200 هرتز. أما إذا تضاعفت كتلته (مع بقاء طوله ثابتاً) فسيكون تواتره 50 هرتز. وهكذا فإن زيادة التواتر بمقدار ثُمانية واحدة (أي أوكتاف واحد) يتطلب مضاعفة قوة الشد أربع مرات. فمن أجل قوة شد To مطبقة على وتر معروف الطول والكتلة، يصدر صوتاً تواتره fo.
ويلخص الجدول (1) قوى الشد اللازمة لرفع طبقة الوتر بمقدار ثمانية واحدة (أوكتاف واحد) أو أكثر فوق f0.
|
||||||||||||||||||||||||