حل المعادلات الاسية Solving Exponential Equations

المعادلات الأسية هي المعادلات التي يكون فيها أحد المتغيرات (x ،y ،z...) في خانة الأس (أعلى رقم أو متغير آخر). أما عن الأسس فهي الأعداد الثابتة الحقيقيّ، لتمثّل المعادلات الأسيّة طريقةً بسيطةً للتعبير عن عملية تكرار الضرب، ويعتمد حل المعادلات الاسية بالأساس على خواصها تلك، والصورة التالية توضح الصيغة الرياضية للمعادلة الأسية:

هذا النوع من المعادلات تتمحور حوله العديد من القوانين والنظريات، وتوجد منها الصور المعقدة والبسيطة، ولكل صورةٍ طريقة حلٍ، وسنناقش هذا معًا.
عناصر المعادلات الأسية
طرق حل المعادلات الاسية
بعد أن عرفنا ما هي المعادلات الأسية، سنتطرق الآن إلى طرق حلها. توجد طريقتان في حل المعادلات الاسية تكون الطريقة الأولى بسيطةً للغاية ولكن تتطلب صيغةً مبسطةً من المعادلة الأسية. أما الطريقة الثانية فتعمل على المعادلات الأسية الأكثر تعقيدًا، ولكنها تتطلب تركيزًا عاليًّا.
حل المعادلات المتساوية الأساس
لنبدأ بالطريقة الأبسط، وهي طريقةٌ تعتمد على حقيقةٍ مرتبطةٍ بالدالة الأسية، وهي أنّه إذا تساوت الأسس؛ فإن الأس يساوي الأس (تتساوى القوى)، بشرط أن يكون الأساس أكبر من صفر، ولا يساوي الواحد.

طبقًا للمذكور أعلاه، فإن حلول هذه الأمثلة تكون كالآتي:
بالرغم من أن طريقة الحل السابقة تعمل مع الأمثلة البسيطة السابقة، إلا أنها لا تعمل مع كل الصيغ البسيطة. انظر إلى المعادلات التالية:

وعلى سبيل المثال فلنتأمل المعادلة (a):

حل المعادلات الأسية عن طريق أخذ لوغاريتم الطرفين
المعادلة السابقة بسيطةٌ للغاية، ولكن لا نستطيع حل المعادلات الاسية من ذلك النمط بالطريقة السابقة، فلا تنطبق عليها القاعدة الخاصة بتساوي الأساسات. لذا فالطريقة الأمثل هنا هي اتخاذ لوغاريتم log الطرفين، وذلك لأن من سمات اللوغاريتمات أنها تنزل الأس من مكانه ليصبح بمعزلٍ عن الأساس تقريبًا. أي أن:
logbar=rlogba
بعد تطبيق الخطوة السابقة على الحد الأيسر للمعادلة الراهنة، يصبح شكل الحد كالتالي: xlog7. وبعد أن وصل شكل الحد لهذا الشكل، يمكن فصل المتغير عن الأعداد ومن ثم حساب قيمته بشكلٍ مباشرٍ.
xlog(7) = log(9)
x = log(9)/log(7)
= 1.1291500
الأمثلة في الصورة السابقة تنطبق عليها طريقة حل المعادلات الاسية السابقة (اتخاذ اللوغاريتم للطرفين)، وسوف نطبق ذلك معًا في المثال (b):
في المثال السابق، استخدمنا الطريقة الثانية الأكثر تعقيدًا في حل المعادلات الاسية لذلك شرحنا لكم خطوات الحل بشكلٍ مفصلٍ منعًا للاتباس. قد يختلف شكل المعادلات الأسية التي تحتاج هذه الطريقة، ولكن الحل واحدٌ، فقط يتطلب الأمر بعض التركيز.
حل المعادلات الاسية عن طريق التحليل لعوامل
هناك طريقة تبسط معظم أشكال المعادلات الأسية وتصل إلى الحل بطريقةٍ سريعةٍ، ولكنها تحتاج بعض الدقة والتركيز، هذه الطريقة تسمى التحليل إلى عواملَ ثلاثيةٍ (Factorise the Trinomial). وهذه الطريقة تعتمد على تحويل شكل المعادلة إلى ثلاثة حدودٍ، حدان في طرفٍ والحد الآخر عبارةٌ عن صفرٍ في الطرف الآخر، والفكرة هي أنّه إذا كان هناك حدان مضروبان وحاصل ضربهما يساوي الصفر، فإن كل حدٍ منهما يساوي الصفر، وبذلك نستطيع العمل على الحد الواحد بشكلٍ منفصلٍ في صورة معادلةٍ أبسط ونصل إلى قيمة المتغير.
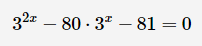
المثال في الصورة السابقة من الأمثلة التي يمكن حل المعادلات الاسية فيها بطريقة تحليل العوامل كما قلنا، وسنرى طريقة الحل الآن: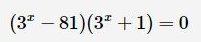
المعادلات الأسية هي المعادلات التي يكون فيها أحد المتغيرات (x ،y ،z...) في خانة الأس (أعلى رقم أو متغير آخر). أما عن الأسس فهي الأعداد الثابتة الحقيقيّ، لتمثّل المعادلات الأسيّة طريقةً بسيطةً للتعبير عن عملية تكرار الضرب، ويعتمد حل المعادلات الاسية بالأساس على خواصها تلك، والصورة التالية توضح الصيغة الرياضية للمعادلة الأسية:
هذا النوع من المعادلات تتمحور حوله العديد من القوانين والنظريات، وتوجد منها الصور المعقدة والبسيطة، ولكل صورةٍ طريقة حلٍ، وسنناقش هذا معًا.
عناصر المعادلات الأسية
- الأساس: وهو الرقم الذي ضُرب في نفسه عددًا معينًا من المرات، ويرمز له مثلًا بالرمز b كما في الصورة الموضحة أعلاه.
- الأس: هو الرقم الذي يعبر عن عدد مرات ضرب الأساس في نفسه، ويرمز له بالرمز x في الصورة السابقة.
- الجذر: هو معكوس الأس، فعلى سبيل المثال؛ الجذر التربيعي للعدد 4 يساوي 2، أما العدد 2 للأس 2 فيساوي 4.
طرق حل المعادلات الاسية
بعد أن عرفنا ما هي المعادلات الأسية، سنتطرق الآن إلى طرق حلها. توجد طريقتان في حل المعادلات الاسية تكون الطريقة الأولى بسيطةً للغاية ولكن تتطلب صيغةً مبسطةً من المعادلة الأسية. أما الطريقة الثانية فتعمل على المعادلات الأسية الأكثر تعقيدًا، ولكنها تتطلب تركيزًا عاليًّا.
حل المعادلات المتساوية الأساس
لنبدأ بالطريقة الأبسط، وهي طريقةٌ تعتمد على حقيقةٍ مرتبطةٍ بالدالة الأسية، وهي أنّه إذا تساوت الأسس؛ فإن الأس يساوي الأس (تتساوى القوى)، بشرط أن يكون الأساس أكبر من صفر، ولا يساوي الواحد.
طبقًا للمذكور أعلاه، فإن حلول هذه الأمثلة تكون كالآتي:
- مثال (a): بما أن الأساس يساوي الأساس وهو 5، فإن الأس يساوي الأس، أي أن 3x=7x-2، بفصل المتغيرات، تصبح المعادلة على هذه الصورة 7x-3x=2، إذن 4x=2، بالقسمة على 4 للطرفين، تكون نتيجة المتغير x هي 0.5. وبذلك يكون حل المعادلة الأسية البسيطة بالطريقة البسيطة الأولى، وبنفس الخطوات تكون باقي الأمثلة في الصورة.
بالرغم من أن طريقة الحل السابقة تعمل مع الأمثلة البسيطة السابقة، إلا أنها لا تعمل مع كل الصيغ البسيطة. انظر إلى المعادلات التالية:
وعلى سبيل المثال فلنتأمل المعادلة (a):
حل المعادلات الأسية عن طريق أخذ لوغاريتم الطرفين
المعادلة السابقة بسيطةٌ للغاية، ولكن لا نستطيع حل المعادلات الاسية من ذلك النمط بالطريقة السابقة، فلا تنطبق عليها القاعدة الخاصة بتساوي الأساسات. لذا فالطريقة الأمثل هنا هي اتخاذ لوغاريتم log الطرفين، وذلك لأن من سمات اللوغاريتمات أنها تنزل الأس من مكانه ليصبح بمعزلٍ عن الأساس تقريبًا. أي أن:
logbar=rlogba
بعد تطبيق الخطوة السابقة على الحد الأيسر للمعادلة الراهنة، يصبح شكل الحد كالتالي: xlog7. وبعد أن وصل شكل الحد لهذا الشكل، يمكن فصل المتغير عن الأعداد ومن ثم حساب قيمته بشكلٍ مباشرٍ.
xlog(7) = log(9)
x = log(9)/log(7)
= 1.1291500
الأمثلة في الصورة السابقة تنطبق عليها طريقة حل المعادلات الاسية السابقة (اتخاذ اللوغاريتم للطرفين)، وسوف نطبق ذلك معًا في المثال (b):
- نقل أحد الحدود إلى الجانب الآخر
بنقل أحد الحدود إلى الجانب الآخر يصبح شكل المعادلة كالتالي:
24y+1 = 3y - أخذ اللوغاريتم للطرفين
بعد أخذ اللوغاريتم للطرفين، يصبح شكل المعادلة كالتالي:
(4y+1)×log(2) = ylog(3) - التعويض بقيمة اللوغاريتم
بالنسبة للوغاريتم 2 ولوغاريتم 3 فهي قيمٌ ثابتةٌ يمكن حسابها من خلال الآلة الحاسبة، فيصبح شكل المعادلة كالتالي:
4y+1)×0.3 = y×0.5) - فك الأقواس
1.2y + 0.3 = 0.5y - فصل المتغيرات والحصول على قيمة المتغير
لنتمكن من الحصول على قيمة المتغير y، يجب أن نجمعه معًا في طرفٍ، والأعداد في طرفٍ آخر:
1.2y – 0.5y = -0.3
0.7y = -0.3
y = -0.428
في المثال السابق، استخدمنا الطريقة الثانية الأكثر تعقيدًا في حل المعادلات الاسية لذلك شرحنا لكم خطوات الحل بشكلٍ مفصلٍ منعًا للاتباس. قد يختلف شكل المعادلات الأسية التي تحتاج هذه الطريقة، ولكن الحل واحدٌ، فقط يتطلب الأمر بعض التركيز.
حل المعادلات الاسية عن طريق التحليل لعوامل
هناك طريقة تبسط معظم أشكال المعادلات الأسية وتصل إلى الحل بطريقةٍ سريعةٍ، ولكنها تحتاج بعض الدقة والتركيز، هذه الطريقة تسمى التحليل إلى عواملَ ثلاثيةٍ (Factorise the Trinomial). وهذه الطريقة تعتمد على تحويل شكل المعادلة إلى ثلاثة حدودٍ، حدان في طرفٍ والحد الآخر عبارةٌ عن صفرٍ في الطرف الآخر، والفكرة هي أنّه إذا كان هناك حدان مضروبان وحاصل ضربهما يساوي الصفر، فإن كل حدٍ منهما يساوي الصفر، وبذلك نستطيع العمل على الحد الواحد بشكلٍ منفصلٍ في صورة معادلةٍ أبسط ونصل إلى قيمة المتغير.
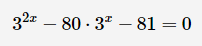
المثال في الصورة السابقة من الأمثلة التي يمكن حل المعادلات الاسية فيها بطريقة تحليل العوامل كما قلنا، وسنرى طريقة الحل الآن:
- أول خطوة هي تحليل المعادلة إلى عواملَ ثلاثيةٍ لتصبح بهذا الشكل:
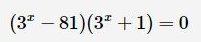
- بعد ذلك يمكننا اختيار أحد الحدين ونساويه بالصفر لنبسط شكل المعادلة، فيصبح 3x - 81 = 0.
- بفصل المتغيرات يصبح شكل المعادلة كالآتي: 3x = 81.
- يمكننا في هذه الحالة أن نجعل الأساسات لنطبق عليها القاعدة الأولى (تساوي الأسس والأساسات)، فيصبح شكل المعادلة كالآتي: 3x = 34.
- بعد أن حولنا الرقم 81 إلى صورةٍ أسيةٍ لنطبق القاعدة، يمكننا استنتاج أن قيمة المتغير x تساوي 4.
- ينطبق الأمر ذاته لاستنباط الحلّ الثاني من العامل الثاني المجاور.
