ما هي انواع القطوع

في الرياضيات لدينا من انواع القطوع أربعة رئيسية، تُسمى بالقطوع المخروطية لأنها ناتجةٌ عن تقاطع مستوي مع مخروطٍ دائريٍّ، وتختلف أشكال هذه القطوع بحسب زاوية وموقع المستوي القاطع للمخروط، وهذه الأنواع الأربعة هي الدوائر، والقطع الناقص، والقطع الزائد، والقطع المكافئ، وجميعها لا تمرّ مستوياتها عبر رأس المخروط.
نلاحظ في الشكل التالي أدناه أنه إذا تم قطع المخروط الدائري بمستوي عمودي على محور المخروط ولا يمر من رأس المخروط يكون التقاطع عبارةً عن دائرةٍ، أما إذا تقاطع المستوي مع المخروط ومحوره ولكن ليس عموديًّا على المحور وغير موازٍ لقاعدته فسينتج عن هذا التقاطع قطع ناقص، ولإنشاء قطع مكافئ يجب أن يكون المستوي موازيًّا لأحد مولدات المخروط وأن يتقاطع مع جهةٍ واحدةٍ من المخروط المزدوج (مخروطين دائريين متقابلين بالرأس حيث يكون محورهما على امتدادٍ واحدٍ)، وأخيرًا لإنشاء قطع زائد يتقاطع المستوي مع المخروط المزدوج بالجهتين ويكون موازيًّا للمحور، وفيما يلي سنشرح كل نوعٍ من انواع القطوع هذه.

القطع المكافئ (Parabola)

أوّل وأشهر انواع القطوع هو القطع المكافئ، وهو رياضيًّا مجموعة من نقاط المستوي التي تبعد عن نقطةٍ معينةٍ F (محرق القطع) بعدًا يساوي بعدها عن مستقيمٍ آخر Δ، وهذا المستقيم ثابت ويسمى دليل القطع، والنقطة F لا تنتمي إلى المستقيم Δ والبعد من الدليل إلى المحرق تعطى بالعلاقة P=2a حيث a هي المسافة بين المحرق وذروة القطع v أو البعج بين الذروة والدليل.
معادلة القطع المكافئ
القطع مفتوح لليمين أو اليسار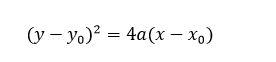
القطع مفتوح للأعلى او الأسفل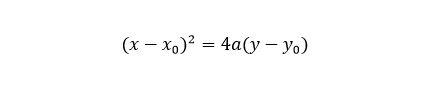
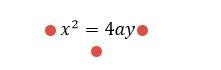
القطع الناقص (Ellipse)

القطع الناقص بيضوي الشكل وهو عبارة عن المنحني المستوي الذي يحقق أن مجموع بُعدَي أي نقطة من هذا المنحني عن نقطتين ثابتتين داخله يبقى ثابتًا، وتدعى هاتان النقطتان بالبؤرتين أو المركزين (F1 وF2)، كما يسمى الخطان a وb بخطَّي توليد القطع وهما اللذان يحددان القطع الناقص.
خصائص القطوع الناقصة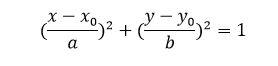
الدائرة (Circle)

إن الدائرة قد لا تُعدّ من انواع القطوع فعليًّا؛ فهي حالةٌ خاصةٌ من القطع الناقص وتتشكل عندما تقع البؤرتان للقطع الناقص في نفس النقطة، وهي عبارةٌ عن مجموعةٍ من نقاط المستوي متساوية البعد عن نقطةٍ واحدةٍ تسمى مركز الدائرة، وليس لديها محاور رئيسية وثانوية لأن جميع أقطارها متساويةً.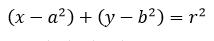
القطع الزائد (Hyperbola)
النوع الأخير من انواع القطوع هو القطع الزائد، وهو المحل الهندسي لنقطة ما تتحرك في المستوى أو مجموعة النقاط التي يكون فرق بعدَي كلّ منها بالقيمة المطلقة عن نقطتين ثابتتين (تدعيان البؤرتين) مقدارًا ثابتًا، ويكون القطع الزائد بشكل منحنيين يشبهان شيئًا ما شكل القطع المكافئ (لكن ليسا قطعين مكافئين) ولكل منهما ذروة ومفتوحان إمّا للأعلى والأسفل، أو لليمين واليسار بحسب محور التناظر للقطع، وتعطى معادلة القطع الزائد بالعلاقة: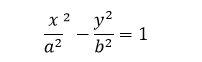
تعدّد استخدامات انواع القطوع
في الرياضيات لدينا من انواع القطوع أربعة رئيسية، تُسمى بالقطوع المخروطية لأنها ناتجةٌ عن تقاطع مستوي مع مخروطٍ دائريٍّ، وتختلف أشكال هذه القطوع بحسب زاوية وموقع المستوي القاطع للمخروط، وهذه الأنواع الأربعة هي الدوائر، والقطع الناقص، والقطع الزائد، والقطع المكافئ، وجميعها لا تمرّ مستوياتها عبر رأس المخروط.
نلاحظ في الشكل التالي أدناه أنه إذا تم قطع المخروط الدائري بمستوي عمودي على محور المخروط ولا يمر من رأس المخروط يكون التقاطع عبارةً عن دائرةٍ، أما إذا تقاطع المستوي مع المخروط ومحوره ولكن ليس عموديًّا على المحور وغير موازٍ لقاعدته فسينتج عن هذا التقاطع قطع ناقص، ولإنشاء قطع مكافئ يجب أن يكون المستوي موازيًّا لأحد مولدات المخروط وأن يتقاطع مع جهةٍ واحدةٍ من المخروط المزدوج (مخروطين دائريين متقابلين بالرأس حيث يكون محورهما على امتدادٍ واحدٍ)، وأخيرًا لإنشاء قطع زائد يتقاطع المستوي مع المخروط المزدوج بالجهتين ويكون موازيًّا للمحور، وفيما يلي سنشرح كل نوعٍ من انواع القطوع هذه.
القطع المكافئ (Parabola)
أوّل وأشهر انواع القطوع هو القطع المكافئ، وهو رياضيًّا مجموعة من نقاط المستوي التي تبعد عن نقطةٍ معينةٍ F (محرق القطع) بعدًا يساوي بعدها عن مستقيمٍ آخر Δ، وهذا المستقيم ثابت ويسمى دليل القطع، والنقطة F لا تنتمي إلى المستقيم Δ والبعد من الدليل إلى المحرق تعطى بالعلاقة P=2a حيث a هي المسافة بين المحرق وذروة القطع v أو البعج بين الذروة والدليل.
معادلة القطع المكافئ
القطع مفتوح لليمين أو اليسار
- في حال كانت إحداثيات ذروته (x0،y0) تكون المعادلة بالشكل:
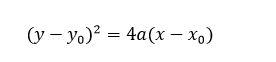
- في حال كانت ذروته تنطبق على محور الإحداثيات تصبح معادلة القطع بالشكل:
القطع مفتوح للأعلى او الأسفل
- في حال كانت إحداثيات ذروته (x0،y0) تكون المعادلة بالشكل:
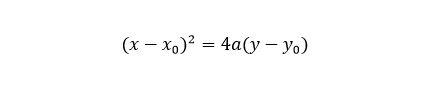
- في حال كانت ذروته تنطبق على مبدأ الإحداثيات تصبح المعادلة بالشكل:
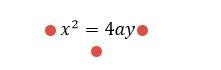
القطع الناقص (Ellipse)
القطع الناقص بيضوي الشكل وهو عبارة عن المنحني المستوي الذي يحقق أن مجموع بُعدَي أي نقطة من هذا المنحني عن نقطتين ثابتتين داخله يبقى ثابتًا، وتدعى هاتان النقطتان بالبؤرتين أو المركزين (F1 وF2)، كما يسمى الخطان a وb بخطَّي توليد القطع وهما اللذان يحددان القطع الناقص.
خصائص القطوع الناقصة
- تعطى معادلة القطع الناقص بالعلاقة:
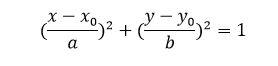
- المركز: هو نقطة داخل القطع الناقص وهي تقع في منتصف الخط الذي يربط بين البؤريين وهو نقطة تقاطع المحاور الرئيسية والثانوية.
- المحور الرئيسي والثانوي: هما أطول وأقصر أقطار القطع الناقص حيث أنّ المحور الرئيسي هو القطر الأطول وطول المحور الرئيسي يساوي مجموع خطي التوليد a وb.
- البؤرتين: هما النقطتان اللتان تحددان القطع الناقص.
الدائرة (Circle)
إن الدائرة قد لا تُعدّ من انواع القطوع فعليًّا؛ فهي حالةٌ خاصةٌ من القطع الناقص وتتشكل عندما تقع البؤرتان للقطع الناقص في نفس النقطة، وهي عبارةٌ عن مجموعةٍ من نقاط المستوي متساوية البعد عن نقطةٍ واحدةٍ تسمى مركز الدائرة، وليس لديها محاور رئيسية وثانوية لأن جميع أقطارها متساويةً.
- معادلة الدائرة في حال كان مركزها يقع في النقطة (a،b) ونصف قطرها r هي:
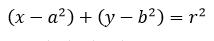
- في حال كان مركزها في مبدأ الإحداثيات تصبح المعادلة بالشكل:
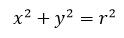
القطع الزائد (Hyperbola)

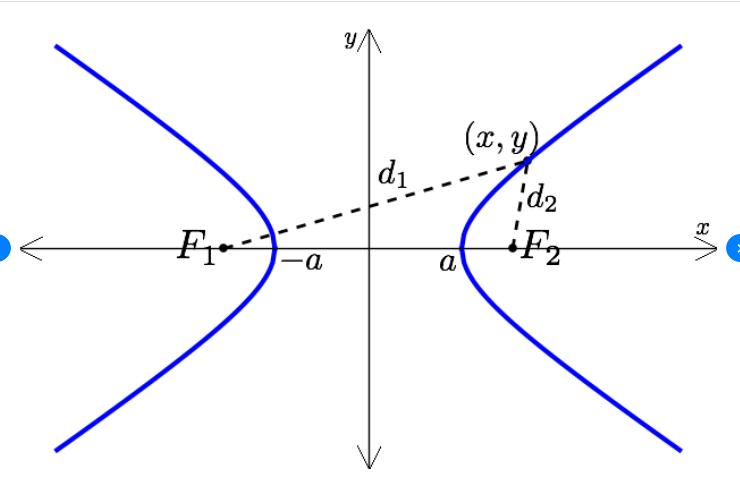
النوع الأخير من انواع القطوع هو القطع الزائد، وهو المحل الهندسي لنقطة ما تتحرك في المستوى أو مجموعة النقاط التي يكون فرق بعدَي كلّ منها بالقيمة المطلقة عن نقطتين ثابتتين (تدعيان البؤرتين) مقدارًا ثابتًا، ويكون القطع الزائد بشكل منحنيين يشبهان شيئًا ما شكل القطع المكافئ (لكن ليسا قطعين مكافئين) ولكل منهما ذروة ومفتوحان إمّا للأعلى والأسفل، أو لليمين واليسار بحسب محور التناظر للقطع، وتعطى معادلة القطع الزائد بالعلاقة:
- في حال كان المحور ينطبق على محور الفواصل x وذروته مبدأ الإحداثيات (مفتوح لليمين واليسار):
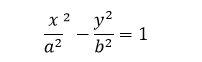
- في حال كان المحور ينطبق على محور التراتيب y (مفتوح للأعلى والأسفل):
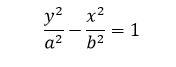
تعدّد استخدامات انواع القطوع
- جميع الكواكب حول الشمس تسير بشكل قطع ناقص حيث تكون الشمس هي إحدى بؤرتَي القطع.
- الأفران الشمسية تستخدم المرايا المكافئة لتجميع أشعة الضوء لاستخدامها بالتسخين، والتي تعتمد على خاصية القطع المكافئ.
- القطع المكافئ يستخدم في تصميم المصابيح الأمامية للسيارة والأضواء الكاشفة لأنه يساعد في تركيز شعاع الضوء.
- يستخدم القطع الزائد في بعض أنظمة الملاحة طويلة المدى المعروفة باسم LORAN.
- تستخدم المرايا المكافئة والعدسات القطعية الزائدة في أنظمة التلسكوبات.
- يستخدم القطع الزائد في المجال العسكري حيث يساعد في تحديد مكان العدو عن طريق تحديد مكان صوت إطلاق النار بواسطة الرادار.
