مساحة الاشكال المركبة (مع أمثلة مشروحة)

قبل الخوض في الحديث عن مساحة الاشكال المركبة عزيزي القارئ، لابدّ أن تعرف ما معنى كلمة مساحة في الأصل، ولماذا نستخدم هذا المصطلح. حقيقةً، المساحة هي واحدة قياس منطقة محصورة في إطارٍ معينٍ، وإن كل مساحات الأشكال الهندسية تُشتَق من مساحة المربع الذي يعتبر أبسط شكلٍ هندسيٍّ، حيث تُحسب مساحته من خلال مربع طول الضلع الواحد، كما أن المساحة هي قيمة الفراغ ثنائي البعد الذي يشغله شكل محدد، وإن معرفتنا بالمساحة وكيفية حساب مساحات الأشكال المختلفة مهمٌ من أجل العديد من المجالات والمواقف التي يمكن أن نمر بها في حياتنا، مثل الزراعة ومجال البناء والعمارة والعلوم المختلفة.
ما هي الاشكال المركبة
من خلال منطق الرياضيات والعلم الرياضي، أصبح بإمكاننا حساب المساحات للأشكال الهندسية المختلفة عن طريق المستوي الديكارتي وحساب عدد مربعاته التي يغطيها الشكل الهندسي المُراد، بحيث يكون كل مربعٍ في المستوي له قياسٌ محددٌ ومعلومٌ، أما الأشكال المركبة، فهي أشكالٌ أكثر تعقيدًا مكونةً من شكلين أو أكثر من الأشكال الهندسية الأساسية والمُتمثّلة في المستطيل والمربع والمثلث والدائرة، وعند حساب مساحة الاشكال المركبة، لا بد من تقسيم الشكل وحساب مساحة كل قسمٍ على حِدى، ولنتذكّر أن:
مساحة الاشكال المركبة
كما أسلفنا الذكر، لحساب مساحة شكلٍ هندسيٍّ مركب، لا بدّ من تقسيم هذا الشكل إلى عدة أشكالٍ بحيث تمكننا من حساب مساحة كل شكلٍ على حدى، وفي النهاية، نجمع مساحة الأشكال الجزئية لنصل إلى النتيجة، وهي مساحة الشكل المركب كاملًا. سنشرح لك في هذا المقال أبرز الأمثلة على حالات الأشكال المركبة وكيفية حلها.
أمثلة على حساب مساحة الاشكال المركبة
المثال الأول

لدينا الشكل المُعطى أعلاه، والذي يعتبر مثالًا بسيطًا على شكلٍ مركبٍ، ففي هذا الشكل لا نستطيع حساب المساحة باستخدام العلاقات البسيطة بشكلٍ مباشرٍ وبسيطٍ مثل طريقة حساب مساحة مربع مثلًا، أو مثلث أو غيرهما من الأشكال الهندسية الأخرى، لذا يجب تقسيمه إلى شكلين أساسيين وهما مستطيلان، لا يمكنك إيجاد مساحة هذا الشكل كما هو بالشكل الحالي، لذا نقوم بحساب مساحة كل مستطيلٍ على حِدى باستخدام الصيغة الأساسية (الطول × العرض)، ثم نجمع المساحتين.
قد يتوارد إلى ذهنك السؤال التالي بعد رؤية الشكل :"هل أقسم الشكل تقسيمًا أفقيًّا أو عموديًّا؟" والجواب هو لا فرق، فكِلا الطريقتين ستعطي نفس النتيجة، لنجرب بالتقسيم العمودي:

لدينا الآن مستطيلان، لحساب مساحة المستطيل الأول نحسب: A1= 9 × 5 = 45cm².
لحساب مساحة المستطيل الثاني نحسب: A2 = 10 × 4 = 40cm².
الآن بعد أن أصبحت لديك مساحة كلا المستطيلين، فما عليك سوى جمعهما معًا لإيجاد مساحة الشكل بالكامل: cm²85= 45 + 40 = A.
ويجب أن تنتبه لاستخدام القياسات الصحيحة المبينة في الشكل للطول والعرض بالنسبة لكل مستطيلٍ (تبين القياسات المستخدمة في مثالنا باللون الأحمر)، وفي حالتنا هذه، الأطوال 15 سم و 5 سم باللون الأسود، غير مطلوبة.
أما في حال اخترت تقسيم الشكل أفقيًّا:

لدينا الآن مستطيل ومربع، لحساب مساحة المربع، نحسب: A1 = 5 × 5 = 25 cm² .
لحساب مساحة المستطيل نحسب: A2 = 15 × 4 = 60cm².
الآن بعد أن أصبحت لديك مساحة كلا المستطيلين، فما عليك سوى جمعهما معًا لإيجاد مساحة الشكل بالكامل: A= 25 + 60 = 85cm². ومرةً أخرى، يجب أن تكون حريصًا أنك تستخدم القياسات الصحيحة..
المثال الثاني
لدينا الشكل التالي مثال آخر على الأشكال المركبة:

الطريقة الأولى لحساب المساحة:
حسب القياسات في الشكل، يمكننا أن نقسمه إلى مستطيلين ومربع واحد، ونحسب مساحة كل مستطيلٍ على حِدى ومساحة المربع، ثم نجمع مساحة الأشكال الثلاثة.
الطريقة الثانية:
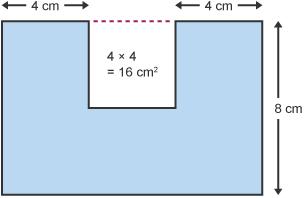
نستطيع اعتبار الشكل عبارةً عن مستطيلٍ واحدٍ طوله (4+4+4=12cm) وعرضه (8cm) وبالتالي مساحته (12×8 = 96cm²)، ثم نطرح من هذه المساحة مساحة المربع الفارغ (4×4= 16cm²)، وبالتالي مساحة الاشكال المركبة هذه مجموعةٌ هو (96 - 16 = 80cm²)..
المثال الثالث
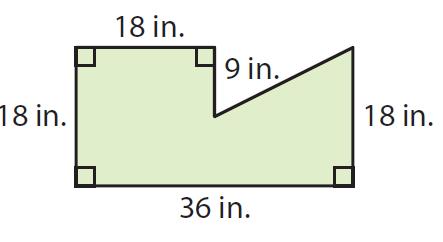
نلاحظ من الشكل المركب التالي أنه يمكن إكمال الرسم ليصبح الشكل مستطيلًا وبداخله مثلث كما في الشكل في الأسفل:

إن طول الضلع (FB = 36 - 18 = 18in)، عندها تصبح مساحة المستطيل ABCD تساوي: (18 × 36 = 648in²)، والآن سنحسب مساحة المثلث FGB انطلاقًا من قانون مساحة المثلث: (القاعدة × الارتفاع ÷ 2)، وبالتالي مساحة المثلث = (9 × 18 ÷ 2 = 81in²)، وبالتالي فإن مساحة الشكل المركب هي: مساحة المستطيل ABCD مطروحًا منه مساحة المثلث FGB، أي (AFGBCD = 648 - 81 = 567 in²).
المثال الرابع والأخير لحساب مساحة الاشكال المركبة
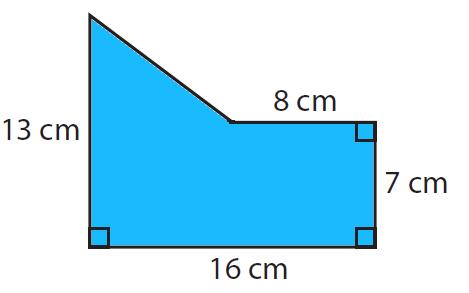
لدينا الشكل أعلاه، ومن الواضح أنه يمكن تقسيمه إلى مستطيلٍ ومثلثٍ بسهولةٍ، حيث نقوم بتمديد الضلع DE فيصبح طول DB يساوي (16 - 8 =8cm) وتصبح BA يساوي (13 - 7 =6cm) كما في الشكل:
ويصبح:
والآن نجمع مساحة المستطيل والمثلث فتصبح مساحة الشكل بالكامل:
112 + 24 = 136 cm²..
قبل الخوض في الحديث عن مساحة الاشكال المركبة عزيزي القارئ، لابدّ أن تعرف ما معنى كلمة مساحة في الأصل، ولماذا نستخدم هذا المصطلح. حقيقةً، المساحة هي واحدة قياس منطقة محصورة في إطارٍ معينٍ، وإن كل مساحات الأشكال الهندسية تُشتَق من مساحة المربع الذي يعتبر أبسط شكلٍ هندسيٍّ، حيث تُحسب مساحته من خلال مربع طول الضلع الواحد، كما أن المساحة هي قيمة الفراغ ثنائي البعد الذي يشغله شكل محدد، وإن معرفتنا بالمساحة وكيفية حساب مساحات الأشكال المختلفة مهمٌ من أجل العديد من المجالات والمواقف التي يمكن أن نمر بها في حياتنا، مثل الزراعة ومجال البناء والعمارة والعلوم المختلفة.
ما هي الاشكال المركبة
من خلال منطق الرياضيات والعلم الرياضي، أصبح بإمكاننا حساب المساحات للأشكال الهندسية المختلفة عن طريق المستوي الديكارتي وحساب عدد مربعاته التي يغطيها الشكل الهندسي المُراد، بحيث يكون كل مربعٍ في المستوي له قياسٌ محددٌ ومعلومٌ، أما الأشكال المركبة، فهي أشكالٌ أكثر تعقيدًا مكونةً من شكلين أو أكثر من الأشكال الهندسية الأساسية والمُتمثّلة في المستطيل والمربع والمثلث والدائرة، وعند حساب مساحة الاشكال المركبة، لا بد من تقسيم الشكل وحساب مساحة كل قسمٍ على حِدى، ولنتذكّر أن:
- مساحة المربع: طول الضلع × طول الضلع.
- مساحة المستطيل: الطول × العرض.
- مساحة المثلث: (1/2) القاعدة × الارتفاع.
- مساحة متوازي الأضلاع: القاعدة × الارتفاع.
- مساحة الدائرة: مربع نصف قطر الدائرة × π.
- مساحة شبه المنحرف: (1/2) مجموع قاعدتي شبه المنحرف المتوازيتين × ارتفاعه.
- مساحة المعين: نصف جداء القطرين، أو جداء الارتفاع في طول أحد الأضلاع..
مساحة الاشكال المركبة
كما أسلفنا الذكر، لحساب مساحة شكلٍ هندسيٍّ مركب، لا بدّ من تقسيم هذا الشكل إلى عدة أشكالٍ بحيث تمكننا من حساب مساحة كل شكلٍ على حدى، وفي النهاية، نجمع مساحة الأشكال الجزئية لنصل إلى النتيجة، وهي مساحة الشكل المركب كاملًا. سنشرح لك في هذا المقال أبرز الأمثلة على حالات الأشكال المركبة وكيفية حلها.
أمثلة على حساب مساحة الاشكال المركبة
المثال الأول
لدينا الشكل المُعطى أعلاه، والذي يعتبر مثالًا بسيطًا على شكلٍ مركبٍ، ففي هذا الشكل لا نستطيع حساب المساحة باستخدام العلاقات البسيطة بشكلٍ مباشرٍ وبسيطٍ مثل طريقة حساب مساحة مربع مثلًا، أو مثلث أو غيرهما من الأشكال الهندسية الأخرى، لذا يجب تقسيمه إلى شكلين أساسيين وهما مستطيلان، لا يمكنك إيجاد مساحة هذا الشكل كما هو بالشكل الحالي، لذا نقوم بحساب مساحة كل مستطيلٍ على حِدى باستخدام الصيغة الأساسية (الطول × العرض)، ثم نجمع المساحتين.
قد يتوارد إلى ذهنك السؤال التالي بعد رؤية الشكل :"هل أقسم الشكل تقسيمًا أفقيًّا أو عموديًّا؟" والجواب هو لا فرق، فكِلا الطريقتين ستعطي نفس النتيجة، لنجرب بالتقسيم العمودي:
لدينا الآن مستطيلان، لحساب مساحة المستطيل الأول نحسب: A1= 9 × 5 = 45cm².
لحساب مساحة المستطيل الثاني نحسب: A2 = 10 × 4 = 40cm².
الآن بعد أن أصبحت لديك مساحة كلا المستطيلين، فما عليك سوى جمعهما معًا لإيجاد مساحة الشكل بالكامل: cm²85= 45 + 40 = A.
ويجب أن تنتبه لاستخدام القياسات الصحيحة المبينة في الشكل للطول والعرض بالنسبة لكل مستطيلٍ (تبين القياسات المستخدمة في مثالنا باللون الأحمر)، وفي حالتنا هذه، الأطوال 15 سم و 5 سم باللون الأسود، غير مطلوبة.
أما في حال اخترت تقسيم الشكل أفقيًّا:
لدينا الآن مستطيل ومربع، لحساب مساحة المربع، نحسب: A1 = 5 × 5 = 25 cm² .
لحساب مساحة المستطيل نحسب: A2 = 15 × 4 = 60cm².
الآن بعد أن أصبحت لديك مساحة كلا المستطيلين، فما عليك سوى جمعهما معًا لإيجاد مساحة الشكل بالكامل: A= 25 + 60 = 85cm². ومرةً أخرى، يجب أن تكون حريصًا أنك تستخدم القياسات الصحيحة..
المثال الثاني
لدينا الشكل التالي مثال آخر على الأشكال المركبة:
الطريقة الأولى لحساب المساحة:
حسب القياسات في الشكل، يمكننا أن نقسمه إلى مستطيلين ومربع واحد، ونحسب مساحة كل مستطيلٍ على حِدى ومساحة المربع، ثم نجمع مساحة الأشكال الثلاثة.
الطريقة الثانية:
نستطيع اعتبار الشكل عبارةً عن مستطيلٍ واحدٍ طوله (4+4+4=12cm) وعرضه (8cm) وبالتالي مساحته (12×8 = 96cm²)، ثم نطرح من هذه المساحة مساحة المربع الفارغ (4×4= 16cm²)، وبالتالي مساحة الاشكال المركبة هذه مجموعةٌ هو (96 - 16 = 80cm²)..

المثال الثالث

نلاحظ من الشكل المركب التالي أنه يمكن إكمال الرسم ليصبح الشكل مستطيلًا وبداخله مثلث كما في الشكل في الأسفل:

إن طول الضلع (FB = 36 - 18 = 18in)، عندها تصبح مساحة المستطيل ABCD تساوي: (18 × 36 = 648in²)، والآن سنحسب مساحة المثلث FGB انطلاقًا من قانون مساحة المثلث: (القاعدة × الارتفاع ÷ 2)، وبالتالي مساحة المثلث = (9 × 18 ÷ 2 = 81in²)، وبالتالي فإن مساحة الشكل المركب هي: مساحة المستطيل ABCD مطروحًا منه مساحة المثلث FGB، أي (AFGBCD = 648 - 81 = 567 in²).
المثال الرابع والأخير لحساب مساحة الاشكال المركبة

لدينا الشكل أعلاه، ومن الواضح أنه يمكن تقسيمه إلى مستطيلٍ ومثلثٍ بسهولةٍ، حيث نقوم بتمديد الضلع DE فيصبح طول DB يساوي (16 - 8 =8cm) وتصبح BA يساوي (13 - 7 =6cm) كما في الشكل:

ويصبح:
- مساحة المثلث: 24 = (6×8)× ABD = 1/2
- مساحة المستطيل: 112 = 7×16 = BEFC
والآن نجمع مساحة المستطيل والمثلث فتصبح مساحة الشكل بالكامل:
112 + 24 = 136 cm²..
