

قصة عدد أويلر e
3 January, 2015
يوجد فى مجتمعاتنا اشخاص يوصفون بانهم النجوم. فهم نجوم الرياضة والفن والسياسة والعلم والتلفاز الى أخره. كذلك توجد وسط الاعداد نجوم! ومثال لهذه النجوم: الأعداد من صفر حتى تسعة. فحيث ان نظام اعدادنا عشرى فاننا نحتاج الي هذه الاعداد العشرة بصفة خاصة لاننا بدلالتها نحصل على باقى الاعداد. كما ان مضاعفات العشرة كالعشرين والثلاثين والمائة والالف والمليون هى ايضا من تلك نجوم. فلغتنا تحتوى على كلمات مخصوصة للتعبير عنها. وهنا الامر منطقى لانه كما سبق وذكرنا فأن هذا يعود الى طبيعة نظام اعدادنا العشرى. لكن هناك بعض النجوم العددية اللتى ليست لها علاقة بالعدد 10 مثل ثابت الدائرة ط (PI) أو ثابت اويلر e. وبينما الامر يعتبر واضحا بالنسبة للثابت ط فهو عدد نعرف فائدته كلنا. وهو عدد قديم استخدمه قدماء المصريين طبعا ليس بالدقة اللتى نعرفها اليوم لكن تم تدقيق قيمته على مر السنوات. لكن الامر بالنسبة للثابت e يبدو مختلفا. فهو ثابت يبدو مجهول الاصل لانعرف وظيفته تحديدا أو كيف تم اكتشافه او لماذا هو مفيد حتى يصير من نجوم الاعداد نخصص من اجله زرا مخصوصا على التنا الحاسبة ونجعله جزءا من دراستنا فى المدارس و الجامعات.
فى الحقيقة ان هذا العدد حديث الاصل نسبيا. فقد ظهر أول ماظهر فى القرن السابع عشر. فليس عمره الاف السنوات كما الثابت ط. وفيما يلى سنتعرف على قصة هذا العدد. ودعونا نقتبس عنوان احد افلام هوليود الكلاسيكية القديمة. فعلى غرار عنوان فيلم: “الطيب والشرس والقبيح” دعونا نتتبع خط عنوانه الحاسب و التحليلى والبنكى والظاهرة و الفيلسوف!
الحاسب ليس حاسبا اليا ولكنه حاسب بشرى. هو الاسكتلندي جون نابيير John Napier اللذي عاش بين 1550 حتى 1617 ميلاديا. وهو مكتشف اللوغاريتم الطبيعى. وقد يظن البعض ان هذا تمهيد منطقى فالثابت e واللوغاريتم الطبيعي هما وجهان لعملة واحدة. مع ذلك علينا ان نكون فى منتهى الحذر فما فهمه نابيير عن حساب اللوغاريتمات ليس ما نفهمه نحن اليوم. وجون نابيير ليس هو مكتشف الثابت e!
نعيش اليوم فى ظل رفاهية استخدام الألات الحاسبة واجهزة الكمبيوتر. لكن فى موضوعنا اليوم علينا ان نعود حتى القرن السادس عشر لنرى كيف كان يحسب الناس فى ذلك الوقت. كانت كل الحسابات تتم عن طريق اليد. وكانت الأعناق مشرأبة الى علم الفلك ومنبهرة بتحديد مواقع النجوم والكواكب فوق قبة السماء. كان الاهتمام بالغا بالقياسات المساحية الجيوديسية كما القياسات الملاحية فى عرض البحر. كان حساب المثلثات هو علم العلوم والاداة الاساس لتحقيق تلك الأهداف. فكان على الفلكيين تحديد جيوب الزوايا جا sin كما جيوب تمام الزوايا جتا cos بمنتهى الدقة. وايضا كان عليهم التعامل مع هذه الارقام العشرية العديدة بمنتهى الدقة.
اليوم طبعا نحصل علي هذه القيم بسرعة فائقة وبدقة عالية وبمنتهى اليسر عن طريق الألات الحاسبة. لكن لم يكن الحال دوما هكذا. واتذكر عندما كنت فى المدرسة كانت توزع علينا دفاتر تحتوى على قيم هذه الدوال وكان التلميذ يبحث عن قيمة جيب الزاوية او جيب تمام الزاوية كما يبحث المرء فى دليل التليفونات او عن معنى كلمة فى المعجم. وفى النهاية يحصل المرء على رقم عشرى مكون من 6 او 7 ارقام عشرية وعليه ان يتعامل مع هذه الارقام يدويا.
كانت قضية نابيير هي كيف يضرب رقم مكون من 7 ارقام عشرية فى رقم اخر مكون من 7 أرقام عشرية. ثم يقسم الناتج على رقم اخر مكون من 7 ارقام عشرية بطريقة مرضية؟ طبعا كان هذا لا يتم عن طريق الألة الحاسبة بل عن طريق اليد. كان الحساب عملية بطيئة مملة تنتج الكثير من الأخطاء. وأراد نابيير ان يصنع ثورة فى طريقة اجراء الحسابات. من أجل هذا اخترع نابيير اللوغاريتم الطبيعي! مرة اخرى مافهمه نابيير عن اللوغاريتم الطبيعى ليس ما نفهمه نحن اليوم. فكأن لسان حال اللوغاريتم يشدو: كنت فى حال وأصبحت فى حال فسبحان مغير الأحوال!
اكتشف نابيير تقنية لتحويل عمليتي الضرب والقسمة البطيئتين الى عمليتى الجمع والطرح الأسرع. كما كان بامكانه تحويل عمليات حساب الجذور المعقدة جدا الى عمليات ضرب أو قسمة بسيطة. وأطلق نابيير على هذه الالية اللوغاريتم Logarithm .وهي كلمة مشتقة من كلمتين يونانيتين: الكلمة الأولى هى Logos ولها اكثر من معنى منها الحكمة او النسبة والكلمة الثانية هي arithmos ومعناها العدد. اذن الكلمة المركبة معناها تقسيم العدد او حكمة العدد!

طريقة حصول نابيير على اللوغاريتمات
وحصل نابيير على لوغاريتماته بطريقة عجيبة وصفها فى كتابه. افترض نابيير كما بالرسم خط مستقيم ذا طول لانهائي يوجد اسفله قطعة مستقيمة محدودة الطول طولها مثلا عشرة مليون متر موازية للخط العلوي. وفائدة الرقم الكبير جعل الناتج عالى الدقة. لنفرض انه يوجد على الخط المستقيم والقطعة المستقيمة جسمان ينزلقان من اليسار الى اليمين. فى بداية الحركة كان الجسمان يوجدان اسفل بعضهما تماما. لنفرض ان الجسم العلوي يتحرك بسرعة ثابتة 1 متر فى الثانية اما الجسم الأخر فانه يبدأ حركته بنفس السرعة ثم يتباطأ دوما بحيث تتناسب سرعته مع طول المسافة المتبقية حتى نهاية القطعة المستقيمة. واطلق نابيير على المسافة المقطوعة على الخط اللانهائى اللوغاريتم. بينما اطلق على المسافة المتبقية -ليست المسافة المقطوعة- على القطعة المستقيمة جيب الزاوية. ثم قام نابيير بوضع قيمة الزاوية اللتى تناسب قيمة جيب الزاوية فى عموده الثالث الأخير.
وقد قام نابيير بملايين العمليات الحسابية واحتاج جدوله الموجود في الرسم الى 20 عاما من العمل المتواصل. فى حقيقة الامر كنت مترددا فى اختيار عنوانا لنابيير. فى النهاية اخترت له عنوان الحاسب لكن ربما يكون من الافضل ان نطلق عليه المثابر!
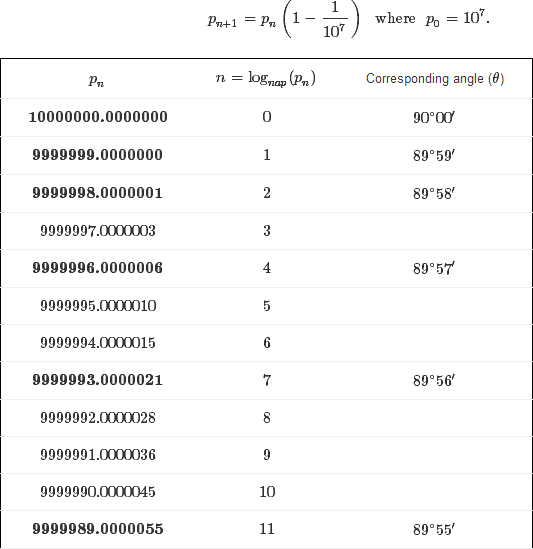
جدول نابيير
وأرقام نابيير تعطى نفس حسابات الألة الحاسبة بعد ان نقسم ارقام العمودين الاول و الثانى على 10 مليون. وبعد ان نعطى اللوغاريتمات اشارة سالبة. ونلاحظ ان نابيير حشر مصطلح جيب الزاوية فى حديثه لانه كان يريد تسليط اكبر قدر من الاهتمام على طريقته.فهو أراد ان يؤكد ان لتقنيته اهمية عملية فى أهم موضوع فى ذلك الوقت ألا وهو حساب المثلثات.
لنرى مثالا عمليا للحساب بلوغاريتمات نابيير: مثلا لو أردنا حساب الجذر التربيعى لضرب عشرة ملايين فى خمسة ملايين:
sqrt(10000000 * 5 000 000)= 7071067.8
علينا ان نبحث عن لوغاريتم عشرة ملايين فى جدول نابيير وكذلك نبحث عن القيمة اللتى تقابل 5 ملايين ثم نجمع القيمتين ونقسم النتيجة على 2 . الان نصل الى الخطوة الاخيرة حيث نبحث عن القيمة اللتى حصلنا عليها فى خانة اللوغاريتمات ونقرأ النتيجة النهائية فى العمود الأول. او
log_nap(10000000)+log_nap(5000000)=0+693147=693147 1
6931471/2 = 3465735
وبالبحث فى الجدول مرة اخرى نجد ان القيمة هى 7071068 وهى نفس القيمة اللتى نحصل عليها عن طريق الألة الحاسبة تقريبا. وعمليات الجمع و القسمة على 2 هى عمليات سهلة بالمقارنة بالضرب ثم البحث عن جذر.
لكن ما السر فى أن طريقة نابيير تعطي القيمة السليمة؟ الاجابة تعتمد على خواص حساب اللوغاريتمات اللتى تحول عمليات الضرب الى جمع و القسمة الى طرح والرفع الى اس الى ضرب. بمعنى أن
log(a*b) = log(a) +log(b) 1
log(a/b) = lob(a) -log(b) 2
log(a^b) = b*log(a) 3
لكن علينا أن نلاحظ أن اللوغاريتمات عند نابيير كانت مجرد ارقام مساعدة لتسهيل عمليات الحساب. ولو استخدمنا الة زمن ورجعنا الى نابيير وقلنا له ما نعرفه عن اللوغاريتمات اليوم وانها دالة وتحديدا انها الدالة العكسية لحساب الأس للثابت e لنظر الينا باستغراب وربما طلب لنا طبيب. فى احسن الاحوال لظن أن جهلنا من طراز فريد. فهو صاحب اللوغاريتمات ومعطيها اسمها ولكنه لا يعرف اى شئ عما نتحدث عنه ولم يكن ذلك هو هدفه.
وكانت لطريقة نابيير اهمية عملية كبيرة. واصبحت الطريقة الرسمية لحساب الارقام الكبيرة والمعقدة. وبناء عليها تم صناعة المسطرة المتحركة ذات القياس اللوغاريتمى. وهذه المسطرة كانت الاداة المحببة لدى المهندسين حتى سبعينيات القرن الماضي. لكن طبعا هذه المسطرة لا تستخدم فى الحسابات اليوم وربما يكون مكانها اليوم هو المتحف!
اذن بالرغم من أن نابيير هو اول من وضع بعض قيم اللوغاريتم الطبيعى الا انه لم يعرف الثابت e . ولذلك اعتقد ان تسمية ذلك العدد بالثابت النيبيري -كما يجد الأنسان احيانا فى بعض المصادر- هى تسمية ليست فى محلها ابدا.
التحليلي: اما التحليلى فهو الهولندي كريستيان هيجينز Christiaan Huygens اللذي عاش فى الفترة بين 1629 حتى 1695 ميلاديا. وهو رياضى وفيزيائى هام. اما عنه نعته بالتحليلى فلانه قم بمقاربة للثابت e عن طريق التحليل analysis أو حساب الدوال. حيث قم هيجنز بدراسة المساحة تحت الدالة الأساسية والمهمة:
f(x) = 1/x 4
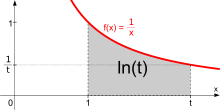
المساحة تساوى قيمة اللوغاريتم الطبيعي
وكما نعلم ان حساب المساحة المحصورة بين محور x ومنحنى الدالة وحدين معينين يمكن الحصول عليها التعويض فى تكامل الدالة بهذين الحدين ثم حساب الفارق . وكما نعلم ان تكامل الدالة 1/x يساوى lnx . وبالتالى فان المساحة المحصورة بين نقطتين 1 و t على محور x يساوى دائما لوعاريتم المتغير t . او تفصيلا:
Integral(1/x) [1->t] =Ln(x) [1->t] = ln(t) -ln(1) = ln(t/1) = ln(t) 5
وهذا هو ماوجده هيجنز. فقد وجد دائما ان المساحة تحت الدالة المحدودة بنقطتين على محور x والنقطة 1 احدهما تساوى دائما قيمة لوغاريتمات نابيير للنقطة الأخرى. بل اكثر من ذلك كان هيجنز يبحث تحديدا عن تلك النقطة اللتى تحصر بينها وبين النقطة 1 مساحة قدرها الوحدة. وكما نعلم ان هذه النقطة لابد ان يكون احداثيها على المحور x يساوى e لأن ln(e) = 1
اذن كان هيجنز يحوم حول e حوما وكاد ان يصل اليه ولكنه ليس هو من حدد قيمة هذا الثابت
البنكى: اما البنكى فهو يأتى من سويسرا بلد البنوك وهو ياكوب برنولي. Jakob Bernoulli . وهو ينتمى الى عائلة برنولى العلمية الشهيرة. وعاش برنولى في الفترة من 1654 حتى 1705 ميلاديا. وكان برنولي مهتما بحساب قيمة الفائدة المركبة. وكان يبحث فى القضية التالية: اذا كان هناك بنك يعطى فائدة 100% . ثم اودع انسان فرنكا سويسريا فى هذه البنك وتركه لمدة عام فكم سوف تصبح قيمته؟ طبعا حساب هذه القيمة سهل ويساوي
1*(1+1) = 2
أي فرنكين.لكن ماذا اذا كان هذا البنك لايعطي فائدة 100% فى السنة ولكنه يعطى 50% مرتين فى السنة. ايضا الحساب سهل ويساوي.
1*(1+0.5)*(1+0.5) = 1*1.5^2= 2.25
وماذا اذا كان البنك يوزع الفائدة بشكل مختلف تحديدا 8.33% كل شهر. مرة اخرى تكون ال 100% موزعة على الاثنى عشر شهرا وستصبح قيمة الفرنك بعد سنة تساوي
1*(1+1/12)^12 = 2.61 فرنكات.
وماذا اذا كان البنك يوزع الفائدة فى كل الأيام على مدار السنة. اذن سوف تكون الفائدة
1*(1+1/365)^365 = 2.71 . وماذا اذا كان البنك يوزع الفائدة كل ساعة بل كل ثانية بل كل لحظة اذن ستصبح قيمة الفرنك تساوى قيمة الثابت e
lim(1+1/n)^n[n->infinity]= e
لكن برنولى لم يستطع التوصل بنفسه الى هذه القيمة. وماتوصل اليه ان القيمة تنحصر بين 2 و 3 .
من ناحية اخرى كان برنولى يبحث ايضا فى اللوغاريتمات وهو ربما اول من ادرك الصورة اللتى نلمكها نحن اليوم حول اللوغاريتمات. وهي أنها الدالة العكسية لحساب الأس. كما ادرك ان لوغاريتمات نابيير لها اساس معين. لكنه لم يدرك ان هذا الاساس هو نفسه النتيجة اللتى يبحث عنها فى حساب الفائدة المركبة الموزعة لحظيا!
الظاهرة: اما الظاهرة فهو ايضا سويسرى كبرنولي هو ليونهارد اويلر Leonhard Euler اللذي عاش فى الفترة بين 1707 حتى 1783 ميلاديا . وكان اويلر اول من حسب قيمة الثابت e وهو من وحد مجهودات سابقيه. فقد كان كل يغنى علي ليلاه لكن اويلر اول من أدرك انهم كلهم يغنون لليلى نفسها ولكنهم لا يدركون ذلك. فهو ادرك ان لوغاريتمات نابيير اساسها هو القيمة اللتى يبحث عنها برنولى وهيجنز وهو من حدد تلك القيمة بدقة ايضا. كان اويلر ظاهرة رياضية فريدة فقد كان له حس عالى بالمعادلات الرياضية وقد اكتشف الكثير من المعادلات الرياضية الجميلة. وفى استفتاء عقدته احدي المجلات الرياضية عن اجمل 10 معادلات رياضية على مستوى التاريخ كانت ثلاث معادلات لاويلر تقبع فى المراكز الخمس الأولى. كما كان المركز الاول من نصيب احد معادلات اويلر. وقد اكتشف اويلر العديد من المعادلات اللتى تحدد قيمة الثابت e منها المعادلة التالية:
e = 1 + 1/1! + 1/2! + 1/3! + … 6
كما اكتشف اويلر العلاقة الجميلة فى الرسم على صورة كسر مستمر واللتى منها نستطيع ان نرى ان هذا الثابت هو عدد غير نسبي
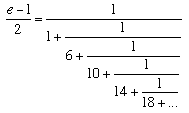
قانون اويلر
كما اننا ندين بالفضل لاويلر لانه هو اول من رمز لهذا العدد بالرمز e . اما سبب التسمية فهو امر فيه اختلاف. البعض يقول لأن هذا اول حرف من اسمه. والبعض يرفض ذلك بشدة. والبعض يقول لان هذا الحرف الأول من كلمة exponential بمعنى أسي والبعض يرفض ذلك بشدة. والبعض يقول لا هذا ولا ذاك ولكن e كان اول حرف متحرك بعد المتغير a وكان اويلر أستخدم بالفعل المتغير a فى معادلاته فاختار e باعتباره التالى ل a . وعموما بغض النظر عن دافع اويلر فقد اتفق الرياضيون على تسمية هذا الرقم بعدد اويلر تخليدا لذكراه.
الفيلسوف: اما الفيلسوف فهو الألمانى كارل فريدرش جاوس Carl Friedrich Gauß اللذى عاش من 1777 حتى 1855 ميلاديا. والمقصود بوصفه بالفيلسوف أنه انسان ذو رؤية شاملة يبحث فى اجماليات الامور ولا يكتفى بالمباشر والسطحى منها ويرى بكل تأكيد ابعد من انفه. كان للثابت e فوائد مباشرة جمة كتسهيل العمليات الحسابية او فى حساب الفائدة البنكية. لكن للدالة e^x خاصية غريبة جدا. فاشتقاقها الأول هو الدالة نفسها. ولهذا فهذه الدالة هى حل المعادلة التفاضلية
y’ = y
والمعادلات التفاضلية هلى لغة العلم والطبيعة. وقبل اكتشاف المعادلات التفاضلية كان عدد القوانين اللتى اكتشفها الانسان محدود جدا. مثل قانون الرافعة او قانون الطفو لارشميدس. لكن بعد اكتشاف المعادلات التفاضلية على يد اسحق نيوتن دخلت البشرية طورا جديدا. وحدثت طفرة وطوفان فى اكتشاف المعادلات الطبيعية. ولذلك تلعب الدالة e^x دورا مهما فى دراسة الانشطارات النووية وحساب الاهتزازات. والثابت e يقع فى قلب هذه الدالة.
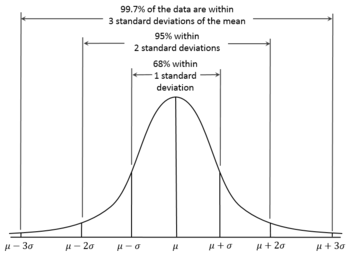
دالة التوزيع الطبيعي
واكتشف جاوس دالة غريبة جدا تقع ايضا e فى قلبها . وهى دالة التوزيع الطبيعي Normal distribution. وهذه الدالة تصف الكثير من الظواهر الطبيعية . بل تصف الاشياء الغير مادية ايضا . فهى تصف توزيع الدخول المادية وطول القامة بل والذكاء على بنى البشر. كما انها تدخل فى بناء النماذج المالية كنموذج بلاك شولتز. كما ان هذه الدالة فى علم الهيدرولوجى تصف توزيع شدة الامطار عبر العام. كما انها تستخدم فى دارسات الاحصاء وحساب الاحتمالات. بل انها تستخدم فى وضع اختبارات قياسية لتحديد مستوى الطلاب.
