كتب الدكتور حازم فلاح سكيك ..يعرفنا على العدسات Lenses

محاضرة 8
العدسات Lenses
الدكتور حازم فلاح سكيك

تعتبر العدسات من اهم الاجهزة البصرية فتجد العدسات في النظارات الطبية والكاميرات والتيليسكوب والمجهر والبريجيكتور،
هناك نوعان من العدسات النوع الاول هو العدسة المحدبة convex lens وتسمي ايضا بالعدسة المجمعة converging lens
والنوع الثاني هو العدسة المقعرة concave lens او العدسة المفرقة diverging lens،
في هذه المحاضرة سندرس فقط العدسات الرقيقة وكيف تكون الصورة. تأتي العدسات بالنوعين السابقين في عدة اشكال حسب تحدب او تقعر سطحي العدسة والشكل التالي يوضح انواع العدسات الرقيقة. وكما كان للمرايا مركز للتقعر وبؤرة كذلك الحال بالنسبة للعدسات حيث ان سطح العدسة هو سطح كروي فله ايضا مركز تقعر وبؤرة، وحيت ان للعدسة سطحين فإن لكل سطح مركز تقعر وبؤرة.لايجاد بؤرة العدسة نقوم بتسليط اشعة ضوئية متوازية من مصدر بعيد جداً مثل اشعة الشمس فنجد ان تلك الاشعة تتجمع في الجانب الأخر من الهدسة ونقطة التجمع هي بؤرة العدسة focus point ويرمز لها بالرمز f وبعدها عن مركز العدسة يسمى البعد البؤري للعدسة focal length. يبين الشكل المقابل سقوط حزة من الأشعة المتوزية على عدسة محدبة convex lens تتجمع في البؤرة وكل شعاع يسقط على العدسة يحدث له انكسار عند سطح العدسة ويحدث انكسار عندما ينفذ الضوء من العدسة محققاً قانون Snell. اعلانات جوجل في حالة العدسة المقعرة concave lens تسقط الأشعة المتوازية على سطح العدسة ولكن تخرج من السطح المقابل متفرقة ولا تتجمع في نقطة كما سبق، ولكن امتداد الاشعة النافذة في اتجاه السطح الأول للعدسة (الخطوط المنقطة في الشكل) تتلاقي في نقطة F وهي بؤرة العدسة في هذه الحالة، وتكون المسافة f وهي البعد البؤري focal length. ملاحظة: تم الاصطلاح على ان يكون البعد البؤري للعدسة المحدبة موجباً والبعد البؤري للعدسة المقعرة سالباً. الطريقة البيانية لتحديد مواصفات الصورة المتكونة بواسطة العدساتيمكن تحديد مواصفات الصورة الناتجة عن العدسات المحدبة أو المقعرة عن طريق الرسم وذلك من خلال تقاطع ثلاث أشعة ضوئية رئيسية كما في الشكل التالي: افترض جسم موجود على مسافة اكبر من البعد البؤري لعدسة محدبة كما في الشكل المقابل، ولتحديد مواصفات الصورة نتبع ما يلي: (a) نرسم شعاع من الجسم موازي للمحور الضوئي للعدسة ليسقط على العدسة وينفذ منكسراً ماراً بالبؤرة F. (الشعاع رقم 1) (b) نرسم شعاع من الجسم يمر في البؤرة ليسقط على العدسة وينفذ موارياً للمحور الضوئي. (الشعاع رقم 2) (c) نرسم شعاع من الجسم ماراً في مركز العدسة فينفذ دون انكسار. (الشعاع رقم 3) لاحظ أن الصورة المتكونة I هي صورة مصغرة مقلوبة وحقيقية. تقاطع الأشعة الثلاثة يحدد موقع الصورة ويمكن تحديد اذا كانت الصورة مكبرة ام مصغرة مقلوبة ام معتدلة وحقيقة او تخيلية وفيما يلي بعض الحالات المختلفة للصورة عند تغير بعد الجسم عن المرأة. اعلانات جوجل نحصل على الصورة المكونة بواسطة العدسة المقعرة بنفس الطريقة التي تكونت بها الصورة في العدسة المحدبة نتبعها. مع العلم ان الصورة تتكون من تقاطع امتداد الاشعة الثلاثة مع بعضها وبالتالي فإن الصورة تكون تخيلية. يوضح الشكل اعلاه علاقة بعد الجسم عن العدسة مع الصورة المكونة على الحائل معادلة العدسات Lenses equation يمكن الخصول على مواصفات الصورة بطريقة رياضية بدلا عن استخدام الطريقة البيانية التي تصبح صعبة عند التعامل مع نظام مكون من أكثر من عدسة.لذلك نستخدم معادلة رياضية تربط بين بعد الجسم عن العدسة do وبعد الصورة عن العدسة di والبعد البؤري للعدسة f. اشتقاق معادلة العدسة افترض جسم على بعد مسافة do من عدسة محدبة بحيث تكون do بين البعد البؤري ونصف قطر التكور radius of curvature كما في الشكل التالي:تتكون صورة الجسم من خلال استخدام شعاعين احدهما يسقط موازيا للمحور الضوئي فينكسر ماراً بالبؤرة والثاني يسقط في مركز العدسة عند النقطة A فينفذ بدون انكسار . نفترض ان طول الجسم ho وطول الصورة الناتجة hi.من المثلثين FI’I و FBA الموضحان في الشكل ادناه بالمنطقة المظللة باللون البرتقالي نجد أنهما متشابهين، اذا نستنتج من ذلك أن


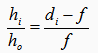
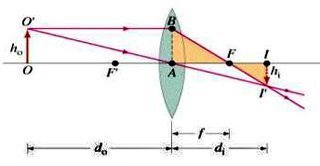
ومن المثلثين O’AO و I’AI المتشابهين ايضاً نحصل على





اعلانات جوجل


بمساواة المعادلتين وقسمة طرفي المعادلة الناتجة على di نحصل على

Lens equation

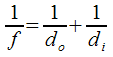
اعلانات جوجل


حيث ان

f = focal length (m)

do = distance from lens to object (m)

di= distance from lens to image (m)

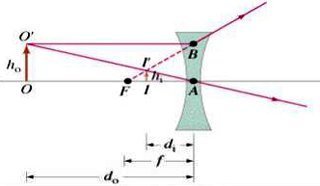
كما يمكن اشتقاق نفس المعادلة بنفس الطريقة باستخدام عدسة مقعرة.



التكبير Magnification

يعرف التكبير m للعدسة بأنه ارتفاع الصورة hi مقسوماً على ارتفاع الجسم ho، فإذا كان التكبير اكبر من واحد فإن الصورة اكبر من الجسم أما اذا كان التكبير اقل من واحد تكون الصورة اصغر من الجسم.



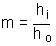
ولكن مما سبق وجدنا ان النسبة بين hi/ho تساوي النسبة بين di/do وبالتالي فإن التكبير يمكن ان يحسب من المعادلة التالية ايضا اذا توفرت المعلومات لذلك بحيث أن



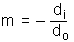
والأشارة السالبة اضيفت لتحقق مفهوم اصطلاح الاشارة الذي سنشرحه في الموضوع القادم. اذا التكبير يعطى بالمعادلة التالية:



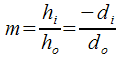
h_i = height of the image (m)
h_o = height of object (m)
m = magnification (how many times bigger or smaller)

اصطلاح الاشارة للعدسات Sign convention for lenses

اشارة كلا من do و di تحدد ما إذا كان الجسم او الصورة حقيقي real او تخيلي virtual، بينما تحدد اشارة التكبير اذا ما كانت الصورة معتدلة upright أو مقلوبة inverted وذلك على النحو التالي:


اما بالنسبة لاشارة كلاً من f و r فتكون على النحو التالي


أما بالنسبة لأشارة التكبير M


سيتضح مفهوم اصطلاح الأشارة من خلال الامثلة المحلولة التالية

---

Example 1