الجبر:
عرف ابن خلدون علم الجبر بأنه من فروع الرياضيات، وأنه صناعة يستخرج بها العدد المجهول من العدد المعلوم إذا كان بينهما صلة تقتضي ذلك. وكان هذا العلم معروفًا لدى الأمم الأخرى ؛ فالإغريق مثلاً كانوا قد توصلوا إلى حل معادلات من الدرجة الثانية، غير أنهم كانوا يجهلون الرموز الجبرية، وكانت طرقهم في ذلك معقدة وغير موحدة. ولم يصبح الجبر علمًا خالصًا إلا بعد أن اشتغل به العرب والمسلمون. كما أن الفضل يعود إلى الرياضيين العرب والمسلمين مثل ابن يونس والحراني وغيرهما في التمهيد لابتكار اللوغاريثمات.
عرف العرب قبل الإسلام نوعًا من الجبر الذي كان يرد في طرائفهم وأشعارهم من قبيل الألغاز، إلا أنهم لم يدونوا ذلك لاعتمادهم على الرواية الشفهية في ضبط كل أمورهم. وقد كثر ذكر المعادلات ذات المجهول الواحد في أشعارهم كقول زرقاء اليمامة:
وصاغ النابغة هذا اللغز في أبيات أخرى فجاءت كما يلي:
وأعظم رياضيي القرن الثالث الهجري، التاسع الميلادي هو محمد بن موسى الخوارزمي، وهو أول من سمّى علم الجبر جبرًا وأول من ألّف في هذا العلم بتشجيع من الخليفة المأمون ؛ فصنّف فيه كتابه المشهور الجبر والمقابلة. ويشهد على عظمة الخوارزمي أن علم الجبر لم يتقدم خلال القرون الثلاثة التي تلت وفاته تقدمًا يذكر.
لم يستخدم الرياضيون الرموز في بادئ الأمر، وإنما جاءت هذه الرموز في حقبة متأخرة نسبياً وعلى يد الرياضيين العرب أنفسهم. فقد بدأت رموز هذا العلم في شكل مصطلحات لغوية ثم تطورت ؛ ومن ذلك استخدام الخوارزمي ومن جاء بعده بقليل المصطلحات الآتية:
الجبر: نقل الحدود المنفية إلى الجانب الآخر من المعادلة.
المقابلة: توحيد الحدود المتماثلة.
الحد: الكمية المعبر عنها في المعادلة بعدد معلوم أو مجهول.
العدد الأصم: الذي لا ينجذر إلا بكسر.
الجذر: كل شيء مضروب في نفسه بدءًا من الواحد إلى أعلى وما دونه من كسور. وهو الحد المجهول في المعادلة ونعبر عنه حالياً بالرمز س، وأطلقوا عليه أيضًا مصطلح الشيء.
جزء الجذر (الشيء): معكوس الجذر ؛ أي 1/س .
المال: كل ما اجتمع من الجذر المضروب في نفسه (س²).
جزء المال: معكوس المال أي 1/س.
العدد المفرد: كل ملفوظ به من العدد بلا نسبة إلى جذور ولا إلى مال.
قسم الخوارزمي المعادلات إلى ستة أقسام كالتالي:
الأموال التي تعدل (تعادل) جذورًا ويقابلها بالرموز الحالية: م س² = ب س.
الأموال التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: م س² = ح.
الجذور التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: ب س = ح.
الأموال والجذور التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: م س² + ب س = ح .
الجذور والأعداد المعلومة التي تعدل أموالاً ويقابلها بالرموز الحالية: ب س + ح = مس² .
الأموال والأعداد التي تعدل جذورًا ويقابلها بالرموز الحالية: م س² + ح = ب س.
ثم تطورت هذه المصطلحات لتحل محلها رموز سهلت استخدام هذا العلم وقادته للتطور، ومن هذه الرموز ما استخدمه القلصادي (ت 891هـ، 1486م) فقد استخدم العلامات التالية:
جـ : لتدل على الجذر ؛ وهو الحرف الأول من كلمة جذر.
ش : لتدل على المجهول ؛ وهو الحرف الأول من كلمة شيء (س).
م : لتدل على مربع المجهول ؛ وهو الحرف الأول من كلمة مال (س²).
ك : لتدل على مكعب المجهول ؛ وهو من حروف كلمة مكعب (س§).
ل : لتدل على المساواة بين الكميتيْن (ل)، وهو من حروف كلمة يعدل.
… ثلاث نقاط للدلالة على النسبة.
المعادلات. يعد حل المعادلات التكعيبية بوساطة قطوع المخروط من أعظم الأعمال التي أسهم بها الرياضيون العرب في هذا العلم. وقد طبقوا نظرياتهم فيها على حلول بعض المسائل الصعبة التي يؤدي حلها إلى معادلات تكعيبية. ومن جملة المسائل التي وردت في تمريناتهم التطبيقية يتبين أنهم كانوا يعرفون حل المعادلات من الدرجة الثانية، كما عرفوا أن لهذه المعادلات جذريْن قاموا باستخراجهما إن كانا موجبين. وتحققوا من الحالة التي يكون فيها الحل مستحيلاً في نطاق الأعداد الحقيقية.
فالخوارزمي يقول في هذا الصدد في كتاب الجبر والمقابلة ¸… واعلم أنك إذا نصفت الأجذار وضربتها في مثلها فكان يبلغ ذلك أقل من الدراهم التي مع المال فالمسألة مستحيلة… وإن كان مثل الدراهم بعينها فجذر المال مثل نصف الأجذار سواء، لا زيادة ولا نقصان…·.
حل العرب معادلات من قوى أعلى ؛ فعلى سبيل المثال نجد أن محمد بن الحسن الكرخي حل معادلات على النمط التالي في كتابه الفخري:
س ¨ + 5س² = 126
و م س2ن + ب سن + حـ = صفر
و س ¨ + م س§ = د
و (100 - س²) (10 + س)² = 8100
والمعادلة الأخيرة حل للمسألة التالية:
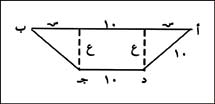
أوجد طول الضلع الرابع المجهول في شبه المنحرف أ ب جـ د الذي فيه أ ب يوازي جـ د، أ د يساوي د جـ يساوي ب جـ يساوي10 والمساحة 90؟
ع = ¬ (100 - س²)
… مساحة أ ب جـ د =
(20 + 2س) ¬ (100 - س²)
أي أن 1/2 ¬ (100 - س²) (10 + س) = 90
وبتربيع الطرفين يكون الناتج:
(100 - س²) (10 + س)² = 8100
(10 + س) ص = 90، حيث ص = ¬( 100 - س²) ؛ أي س² + ص² = 100
أما معادلات الدرجة الثانية فقد وردت فيها مسائل كثيرة في كتبهم منها على سبيل المثال المعادلات التالية:
س² + ص = ط² و ص² + س = ن²
و س ص + س = ط² و س ص + ص = ن²
ولعل الرياضيين العرب هم أول من استعان بالهندسة لحل المعادلات الجبرية من الدرجة الثانية، وهذا من طرق الهندسة التحليلية ؛ ولثابت بن قرة في ذلك ابتكارات لم يسبق إليها، فقد وضع كتابًا في الجبر بيَّن فيه علاقة الجبر بالهندسة وكيفية الجمع بينهما. كما وردت مسائل لدى الخوارزمي وغيره من الرياضيين العرب استخدموا فيها الهندسة لحل مسائل الجبر من ذلك ما ورد لدى الخوارزمي في حل المعادلات التالية هندسيًا:
س² + 10س = 39
س² + 21 = 10س
س² = 3 س + ع
فلحل المعادلة الأولى على سبيل المثال: نفترض أن المستقيم جـ ب = س ، ثم نقيم عليه المربع أ ب جـ د ونمد د جـ إلى م، و د أ إلى هـ بحيث يكون أ هـ مساويًا لـ جـ م =1/2 × 10 = 5 ثم نكمل الرسم كما هو موضح.
من المساحات الموضحة، والمعادلة
س² + 10س = 39
نجد: س² + 10س + 25 = 39 + 25 = 64
وهي مساحة المربع د هـ ع م
… ضلعه يساوي 8
… س = 8 - 5 = 3
عني الرياضيون العرب أيضًا بالجذور الصّماء، وبحثوا في نظرية ذات الحدين التي يمكن بوساطتها رفع المقدار الجبري ذي الحدين إلى قوة معلومة أُسها عدد صحيح موجب. أما في الجذور الصم ؛ فقد كان الخوارزمي أول من استعمل كلمة أصم للإشارة إلى العدد الذي لا جذر له. وأوجد العرب طرقًا لإيجاد قيم تقريبية للأعداد التي ليس لها جذور ؛ فبهاء الدين العاملي يقول في الخلاصة: ¸وإن كان أصم فأسقط منه أقرب المجذورات إليه، وانسب الباقي إلى مضعّف جذر المُسقط مع الواحد، فجذر المُسقط مع حاصل النسبة هو جذر الأصم بالتقريب·. فلو افترضنا أن العدد الأصم في هذ الحالة (م)، وكان أقرب عدد له جذر تربيعي هو (ب²) وكان الفرق يساوي (هـ) لذا فإن:
م - ب² = هـ
وعلى هذا يكون ¬ م = ب + ه/2ب+1
فعلى سبيل المثال ¬ 10= 3 + 1/2×3+1 = 3 + 1/7 = 1/7 3.
عرف ابن خلدون علم الجبر بأنه من فروع الرياضيات، وأنه صناعة يستخرج بها العدد المجهول من العدد المعلوم إذا كان بينهما صلة تقتضي ذلك. وكان هذا العلم معروفًا لدى الأمم الأخرى ؛ فالإغريق مثلاً كانوا قد توصلوا إلى حل معادلات من الدرجة الثانية، غير أنهم كانوا يجهلون الرموز الجبرية، وكانت طرقهم في ذلك معقدة وغير موحدة. ولم يصبح الجبر علمًا خالصًا إلا بعد أن اشتغل به العرب والمسلمون. كما أن الفضل يعود إلى الرياضيين العرب والمسلمين مثل ابن يونس والحراني وغيرهما في التمهيد لابتكار اللوغاريثمات.
عرف العرب قبل الإسلام نوعًا من الجبر الذي كان يرد في طرائفهم وأشعارهم من قبيل الألغاز، إلا أنهم لم يدونوا ذلك لاعتمادهم على الرواية الشفهية في ضبط كل أمورهم. وقد كثر ذكر المعادلات ذات المجهول الواحد في أشعارهم كقول زرقاء اليمامة:
|
وصاغ النابغة هذا اللغز في أبيات أخرى فجاءت كما يلي:
|
وأعظم رياضيي القرن الثالث الهجري، التاسع الميلادي هو محمد بن موسى الخوارزمي، وهو أول من سمّى علم الجبر جبرًا وأول من ألّف في هذا العلم بتشجيع من الخليفة المأمون ؛ فصنّف فيه كتابه المشهور الجبر والمقابلة. ويشهد على عظمة الخوارزمي أن علم الجبر لم يتقدم خلال القرون الثلاثة التي تلت وفاته تقدمًا يذكر.
لم يستخدم الرياضيون الرموز في بادئ الأمر، وإنما جاءت هذه الرموز في حقبة متأخرة نسبياً وعلى يد الرياضيين العرب أنفسهم. فقد بدأت رموز هذا العلم في شكل مصطلحات لغوية ثم تطورت ؛ ومن ذلك استخدام الخوارزمي ومن جاء بعده بقليل المصطلحات الآتية:
الجبر: نقل الحدود المنفية إلى الجانب الآخر من المعادلة.
المقابلة: توحيد الحدود المتماثلة.
الحد: الكمية المعبر عنها في المعادلة بعدد معلوم أو مجهول.
العدد الأصم: الذي لا ينجذر إلا بكسر.
الجذر: كل شيء مضروب في نفسه بدءًا من الواحد إلى أعلى وما دونه من كسور. وهو الحد المجهول في المعادلة ونعبر عنه حالياً بالرمز س، وأطلقوا عليه أيضًا مصطلح الشيء.
جزء الجذر (الشيء): معكوس الجذر ؛ أي 1/س .
المال: كل ما اجتمع من الجذر المضروب في نفسه (س²).
جزء المال: معكوس المال أي 1/س.
العدد المفرد: كل ملفوظ به من العدد بلا نسبة إلى جذور ولا إلى مال.
قسم الخوارزمي المعادلات إلى ستة أقسام كالتالي:
الأموال التي تعدل (تعادل) جذورًا ويقابلها بالرموز الحالية: م س² = ب س.
الأموال التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: م س² = ح.
الجذور التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: ب س = ح.
الأموال والجذور التي تعدل عددًا معلومًا ويقابلها بالرموز الحالية: م س² + ب س = ح .
الجذور والأعداد المعلومة التي تعدل أموالاً ويقابلها بالرموز الحالية: ب س + ح = مس² .
الأموال والأعداد التي تعدل جذورًا ويقابلها بالرموز الحالية: م س² + ح = ب س.
ثم تطورت هذه المصطلحات لتحل محلها رموز سهلت استخدام هذا العلم وقادته للتطور، ومن هذه الرموز ما استخدمه القلصادي (ت 891هـ، 1486م) فقد استخدم العلامات التالية:
جـ : لتدل على الجذر ؛ وهو الحرف الأول من كلمة جذر.
ش : لتدل على المجهول ؛ وهو الحرف الأول من كلمة شيء (س).
م : لتدل على مربع المجهول ؛ وهو الحرف الأول من كلمة مال (س²).
ك : لتدل على مكعب المجهول ؛ وهو من حروف كلمة مكعب (س§).
ل : لتدل على المساواة بين الكميتيْن (ل)، وهو من حروف كلمة يعدل.
… ثلاث نقاط للدلالة على النسبة.
المعادلات. يعد حل المعادلات التكعيبية بوساطة قطوع المخروط من أعظم الأعمال التي أسهم بها الرياضيون العرب في هذا العلم. وقد طبقوا نظرياتهم فيها على حلول بعض المسائل الصعبة التي يؤدي حلها إلى معادلات تكعيبية. ومن جملة المسائل التي وردت في تمريناتهم التطبيقية يتبين أنهم كانوا يعرفون حل المعادلات من الدرجة الثانية، كما عرفوا أن لهذه المعادلات جذريْن قاموا باستخراجهما إن كانا موجبين. وتحققوا من الحالة التي يكون فيها الحل مستحيلاً في نطاق الأعداد الحقيقية.
فالخوارزمي يقول في هذا الصدد في كتاب الجبر والمقابلة ¸… واعلم أنك إذا نصفت الأجذار وضربتها في مثلها فكان يبلغ ذلك أقل من الدراهم التي مع المال فالمسألة مستحيلة… وإن كان مثل الدراهم بعينها فجذر المال مثل نصف الأجذار سواء، لا زيادة ولا نقصان…·.
حل العرب معادلات من قوى أعلى ؛ فعلى سبيل المثال نجد أن محمد بن الحسن الكرخي حل معادلات على النمط التالي في كتابه الفخري:
س ¨ + 5س² = 126
و م س2ن + ب سن + حـ = صفر
و س ¨ + م س§ = د
و (100 - س²) (10 + س)² = 8100
والمعادلة الأخيرة حل للمسألة التالية:
أوجد طول الضلع الرابع المجهول في شبه المنحرف أ ب جـ د الذي فيه أ ب يوازي جـ د، أ د يساوي د جـ يساوي ب جـ يساوي10 والمساحة 90؟
 |
ع = ¬ (100 - س²)
… مساحة أ ب جـ د =
(20 + 2س) ¬ (100 - س²)
أي أن 1/2 ¬ (100 - س²) (10 + س) = 90
وبتربيع الطرفين يكون الناتج:
(100 - س²) (10 + س)² = 8100
(10 + س) ص = 90، حيث ص = ¬( 100 - س²) ؛ أي س² + ص² = 100
أما معادلات الدرجة الثانية فقد وردت فيها مسائل كثيرة في كتبهم منها على سبيل المثال المعادلات التالية:
س² + ص = ط² و ص² + س = ن²
و س ص + س = ط² و س ص + ص = ن²
ولعل الرياضيين العرب هم أول من استعان بالهندسة لحل المعادلات الجبرية من الدرجة الثانية، وهذا من طرق الهندسة التحليلية ؛ ولثابت بن قرة في ذلك ابتكارات لم يسبق إليها، فقد وضع كتابًا في الجبر بيَّن فيه علاقة الجبر بالهندسة وكيفية الجمع بينهما. كما وردت مسائل لدى الخوارزمي وغيره من الرياضيين العرب استخدموا فيها الهندسة لحل مسائل الجبر من ذلك ما ورد لدى الخوارزمي في حل المعادلات التالية هندسيًا:
س² + 10س = 39
س² + 21 = 10س
س² = 3 س + ع
فلحل المعادلة الأولى على سبيل المثال: نفترض أن المستقيم جـ ب = س ، ثم نقيم عليه المربع أ ب جـ د ونمد د جـ إلى م، و د أ إلى هـ بحيث يكون أ هـ مساويًا لـ جـ م =1/2 × 10 = 5 ثم نكمل الرسم كما هو موضح.
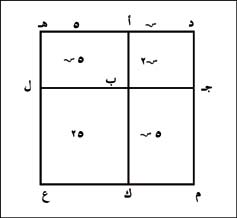 |
س² + 10س = 39
نجد: س² + 10س + 25 = 39 + 25 = 64
وهي مساحة المربع د هـ ع م
… ضلعه يساوي 8
… س = 8 - 5 = 3
عني الرياضيون العرب أيضًا بالجذور الصّماء، وبحثوا في نظرية ذات الحدين التي يمكن بوساطتها رفع المقدار الجبري ذي الحدين إلى قوة معلومة أُسها عدد صحيح موجب. أما في الجذور الصم ؛ فقد كان الخوارزمي أول من استعمل كلمة أصم للإشارة إلى العدد الذي لا جذر له. وأوجد العرب طرقًا لإيجاد قيم تقريبية للأعداد التي ليس لها جذور ؛ فبهاء الدين العاملي يقول في الخلاصة: ¸وإن كان أصم فأسقط منه أقرب المجذورات إليه، وانسب الباقي إلى مضعّف جذر المُسقط مع الواحد، فجذر المُسقط مع حاصل النسبة هو جذر الأصم بالتقريب·. فلو افترضنا أن العدد الأصم في هذ الحالة (م)، وكان أقرب عدد له جذر تربيعي هو (ب²) وكان الفرق يساوي (هـ) لذا فإن:
م - ب² = هـ
وعلى هذا يكون ¬ م = ب + ه/2ب+1
فعلى سبيل المثال ¬ 10= 3 + 1/2×3+1 = 3 + 1/7 = 1/7 3.
