تويت
الزاوية الذهبية
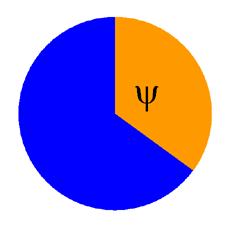
الزاوية الذهبية
في الهندسة الرياضية، تعرف الزاوية الذهبية على أنها الزاوية المركزية التي نصنعها عندما نقسم محيط الدائرة إلى قطاع a و قطاع صغير b بحيث يتحقق :
c = a + b {\displaystyle c=a+b\,}
و
c a = a b {\displaystyle {\frac {c}{a}}={\frac {a}{b}}}
الزاوية المنشأة عن طريق القوس b للدائرة تسمى الزاوية الذهبية. و قياسها تقريبا 137.51° أي ما يعادل 2.4000 راديان. و هي مشتقة من الرقم الذهبي (φ)
القياس الدقيق بالراديان هو:
حيث φ {\displaystyle \varphi \,\!}
هو الرقم الذهبي φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\,\!} 
.
الزاوية الذهبية في الطبيعة
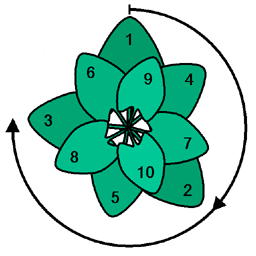
الزاوية بين الوريقات المتتالية لتويج بعض الزهور هي الزاوية الذهبية
نجد هذه الزاوية بكثرة في الطبيعة. و لعل أشد مثال مدعاة للذهول هو "تفاحة الصنوبر"، التي نجد عليها لوالب أرخميدس التي تكون نقاط تقاطعها مصفوفة حسب الزاوية الذهبية.
الزاوية الذهبية
في الهندسة الرياضية، تعرف الزاوية الذهبية على أنها الزاوية المركزية التي نصنعها عندما نقسم محيط الدائرة إلى قطاع a و قطاع صغير b بحيث يتحقق :
c = a + b {\displaystyle c=a+b\,}
و
c a = a b {\displaystyle {\frac {c}{a}}={\frac {a}{b}}}
الزاوية المنشأة عن طريق القوس b للدائرة تسمى الزاوية الذهبية. و قياسها تقريبا 137.51° أي ما يعادل 2.4000 راديان. و هي مشتقة من الرقم الذهبي (φ)
القياس الدقيق بالراديان هو:
- 2 π φ {\displaystyle {\frac {2\pi }{\varphi }}\,\!}
للزاوية الداخلية
- 2 π φ + 1 {\displaystyle {\frac {2\pi }{\varphi +1}}\,\!}
للزاوية الخارجية
حيث φ {\displaystyle \varphi \,\!}
هو الرقم الذهبي φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\,\!} .الزاوية الذهبية في الطبيعة
الزاوية بين الوريقات المتتالية لتويج بعض الزهور هي الزاوية الذهبية
نجد هذه الزاوية بكثرة في الطبيعة. و لعل أشد مثال مدعاة للذهول هو "تفاحة الصنوبر"، التي نجد عليها لوالب أرخميدس التي تكون نقاط تقاطعها مصفوفة حسب الزاوية الذهبية.
