قاعدة لايبنيز العامة
تلعب مشتقات الاقترانات دورا أساسيا في حساب التفاضل والتكامل وتطبيقاتها. على وجه الخصوص، ويمكن استخدامها لدراسة هندسة المنحنيات، وإيجاد القيم المُثلى للاقترانات، وصياغة المعادلات التفاضلية التي توفر نماذج رياضية في مجالات عدة مثل الفيزياء والكيمياء والبيولوجيا والتمويل.
ظهرت فكرة المشتقة لأول مرة من قبل المحامي والرياضي الشهير بيير دي فيرما (1601-1665) لحل العديد من المسائل مثل العثور على المماس لمنحنى عند نقطة. وبحلول العام 1670 وما بعده، أسس إسحق نيوتن (1642-1727) وغوتفريد لايبنيز (1646-1716) لعلم التفاضل والتكامل الحديث وذلك بإدخال المفاهيم العامة للتفاضل والتكامل وآلية حساب كل منهما خصوصا أن كل منهما عملية معكوسة للأخرى، كما تم وضع نظام ترميز سهل ومبسط لكل منهما وما زال العمل به جارياً حتى وقتنا الحالي.
في علم التفاضل والتكامل، يمكن تعميم مشتقة حاصل الجمع، الضرب، والاقترانات المركبة أو ما يعرف بقاعدة السلسلة، بشكل جيد ومن أي رتبة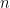 من المشتقات.مشتقة حاصل جمع اقترانين هي الأسهل، حيث إنّ مشتقة
من المشتقات.مشتقة حاصل جمع اقترانين هي الأسهل، حيث إنّ مشتقة  من أي رتبة
من أي رتبة 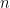 هي ببساطة حاصل جمع المشتقات من نفس الرتبة،
هي ببساطة حاصل جمع المشتقات من نفس الرتبة،  . قاعدة لايبنيز العامة، عبارة عن تعميم للمشتقة من الرتبة
. قاعدة لايبنيز العامة، عبارة عن تعميم للمشتقة من الرتبة 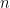 لحاصل ضرب اقترانين، وتنص على أنه إذا كان كل من الاقترانين
لحاصل ضرب اقترانين، وتنص على أنه إذا كان كل من الاقترانين  و
و قابلاً للاشتقاق
قابلاً للاشتقاق 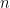 من المرات، فإن حاصل ضربهما
من المرات، فإن حاصل ضربهما  عبارة عن اقتران قابل للاشتقاق أيضاً من المرات، ومشتقته من الرتبة
عبارة عن اقتران قابل للاشتقاق أيضاً من المرات، ومشتقته من الرتبة 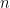 تُعطى بالعلاقة:
تُعطى بالعلاقة:

حيث هو معامل ذات الحدّين، و
هو معامل ذات الحدّين، و  . فعلى سبيل المثال، فإن المشتقة الأولى لحاصل الضرب
. فعلى سبيل المثال، فإن المشتقة الأولى لحاصل الضرب تُعطى بالعلاقة:
تُعطى بالعلاقة:

المشتقة الثانية
يمكن حساب المشتقة الثانية للاقتران إذا عُلمت مشتقته الأولى $latex f'(x) $ وذلك باشتقاق المشتقة الأولى للاقتران
إذا عُلمت مشتقته الأولى $latex f'(x) $ وذلك باشتقاق المشتقة الأولى للاقتران  مرة ثانية، أي أن
مرة ثانية، أي أن

بما أن فإن
فإن

وبتطبيق قاعدة لايبنيتز، نجد أن

برهان القاعدة
يمكن برهان قاعدة لايبنيز باستخدام مبدأ الاستقراء الرياضي. لتكن

1. القاعدة صحيحة عندما m=1. وذلك لأن

2. نفرض أن القاعدة

صحيحة لأي عدد صحيح m≥1.
3. المطلوب الآن برهان صحة العلاقة لمشتقة من الرتبة (m+1)، وهذا يتم على النحو التالي:

تعميم القاعدة لأكثر من اقترانين
لتكن f1. f2. …. fm مجموعة من الاقترانات القابلة للاشتقاق n من المرات، فإن حاصل الضرب f1f2…fm قابل للاشتقاق n من المرات، كذلك

حيث

فعلى سبيل المثال، المشتقة الثانية للاقتران يمكن حسابها باستخدام تعميم قاعدة لايبنيز كما يلي.
يمكن حسابها باستخدام تعميم قاعدة لايبنيز كما يلي.

تلعب مشتقات الاقترانات دورا أساسيا في حساب التفاضل والتكامل وتطبيقاتها. على وجه الخصوص، ويمكن استخدامها لدراسة هندسة المنحنيات، وإيجاد القيم المُثلى للاقترانات، وصياغة المعادلات التفاضلية التي توفر نماذج رياضية في مجالات عدة مثل الفيزياء والكيمياء والبيولوجيا والتمويل.
ظهرت فكرة المشتقة لأول مرة من قبل المحامي والرياضي الشهير بيير دي فيرما (1601-1665) لحل العديد من المسائل مثل العثور على المماس لمنحنى عند نقطة. وبحلول العام 1670 وما بعده، أسس إسحق نيوتن (1642-1727) وغوتفريد لايبنيز (1646-1716) لعلم التفاضل والتكامل الحديث وذلك بإدخال المفاهيم العامة للتفاضل والتكامل وآلية حساب كل منهما خصوصا أن كل منهما عملية معكوسة للأخرى، كما تم وضع نظام ترميز سهل ومبسط لكل منهما وما زال العمل به جارياً حتى وقتنا الحالي.
في علم التفاضل والتكامل، يمكن تعميم مشتقة حاصل الجمع، الضرب، والاقترانات المركبة أو ما يعرف بقاعدة السلسلة، بشكل جيد ومن أي رتبة

حيث

المشتقة الثانية
يمكن حساب المشتقة الثانية للاقتران

بما أن

وبتطبيق قاعدة لايبنيتز، نجد أن

برهان القاعدة
يمكن برهان قاعدة لايبنيز باستخدام مبدأ الاستقراء الرياضي. لتكن

1. القاعدة صحيحة عندما m=1. وذلك لأن

2. نفرض أن القاعدة

صحيحة لأي عدد صحيح m≥1.
3. المطلوب الآن برهان صحة العلاقة لمشتقة من الرتبة (m+1)، وهذا يتم على النحو التالي:

تعميم القاعدة لأكثر من اقترانين
لتكن f1. f2. …. fm مجموعة من الاقترانات القابلة للاشتقاق n من المرات، فإن حاصل الضرب f1f2…fm قابل للاشتقاق n من المرات، كذلك

حيث

فعلى سبيل المثال، المشتقة الثانية للاقتران

