تُعد نظرية الألعاب -أو كما تُسمى نظرية الاستراتيجية المثلى- التجسيد الفعلي للتفاعل الاستراتيجي بين منافسين أو أكثر ضمن موقف يضم نتائج وقواعد محددة، وبالرغم من استخدام هذه النظرية في العديد من فروع المعرفة يلاحظ استخدامها الأبرز في الأدوات المستخدمة في الدراسات الاقتصادية، إذ من الممكن أن يكون التطبيق الاقتصادي لهذه النظرية وسيلة هامة للمساعدة في التحليل الأساسي ضمن الصناعات والقطاعات وأي تفاعل استراتيجي بين مؤسستين أو أكثر.
يقدم هذا المقال نظرة تعريفية لنظرية الألعاب ومصطلحاتها الأساسية، إضافةً لطرح أسلوب بسيط لحل الألعاب الرياضية يطلق عليها اصطلاحًا مفهوم الاستقراء الارتجاعي.
مفاهيم متعلقة بنظرية الألعاب الرياضية
يمكن استخدام نظرية الألعاب للمساعدة في تحديد النتائج المرجح حدوثها في الحالات التي تتضمن منافسين أو أكثر مع وجود نتائج ومخرجات معروفة وقابلة للقياس الكمي. فيما يلي تعريفات بعض المصطلحات الشائعة المستخدمة في نظرية الألعاب الرياضية:
من ضمن المفاهيم الاقتصادية الهامة، يعد مصطلح العقلانية والتعظيم من المصطلحات الاقتصادية الهامة لنظرية الألعاب، لهذا السبب يفترض تمتع المنافسين في اللعبة بتفكير عقلاني مع سعيهم لتعظيم مكاسبهم، وعند معاينة الألعاب القائمة يفترض بالنيابة عن المنافس أن تتضمن المكاسب المُدرجة مجموع كافة الأرباح المرتبطة بالنتائج، وهذا الإجراء يقصي كافة الأسئلة من نوع « ماذا لو؟» التي يمكن أن تظهر ضمن عملية اتخاذ القرار.
الجدير بالذكر أنه يمكن نظريًا لعدد اللاعبين أن يكون لا نهائيًا لكن غالبًا ما ينحصر مفهوم معظم الألعاب ضمن سياق التنافس الثنائي، لهذا السبب تعد اللعبة المتسلسلة المؤلفة من متنافسين اثنين واحدة من أبسط الأمثلة على هذه النظرية.
نموذج لحل الألعاب المتسلسلة بالاستقراء الارتجاعي
يمثل المخطط في الصورة أدناه مثالًا بسيطًا للعبة متسلسلة بين منافسين اثنين، فنجد في المقدمة التسميات للمنافس الأول والثاني وضمن هذه التسميات نجد مجموعة المعلومات لكلا المنافسين على التوالي، وتمثل الأرقام ضمن الأقواس في أسفل المخطط النتائج المحققة عند نقطة معينة، الجدير بالذكر أن اللعبة متسلسلة ما يعني أن اللاعب الأول سيتخذ القرار الأول(يسار أو يمين) وبعد ذلك يتخذ اللاعب الثاني القرار (أعلى أوأسفل).
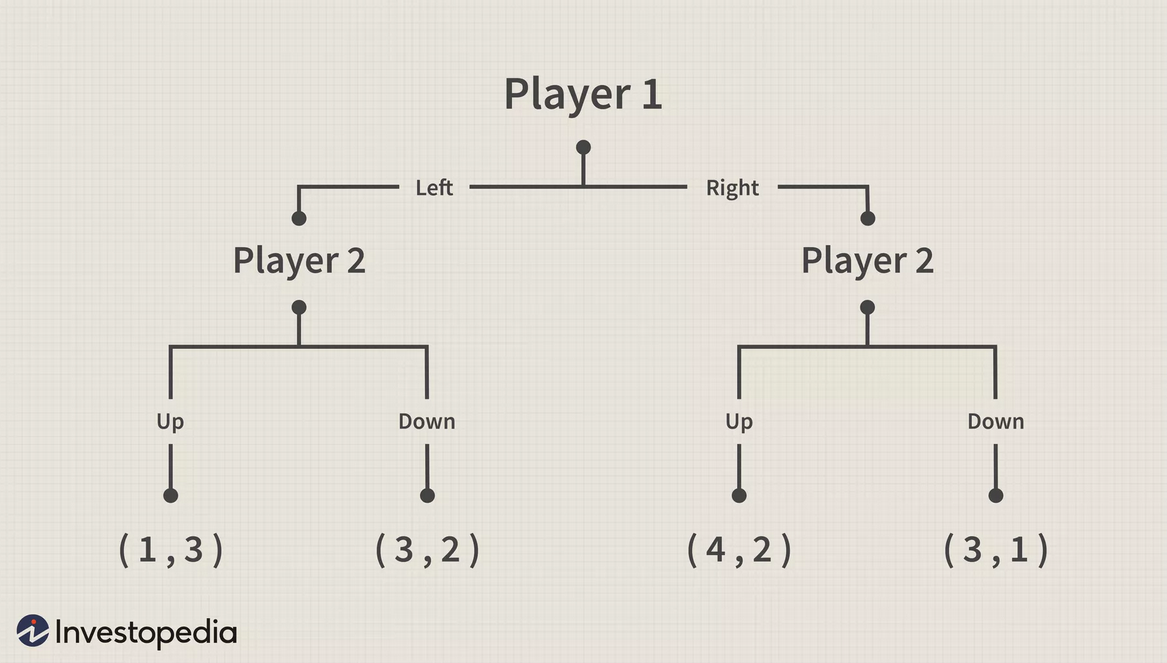
يستخدم مفهوم الاستقراء الارتجاعي مثل جميع مفاهيم نظرية الألعاب مبادئ العقلانية والتعظيم، ما يعني أن المنافس الثاني سيحاول تعظيم مكاسبه في جميع الأحوال الممكنة، ولمجموعتي المعلومات خياران اثنان والمجموع الكلي أربعة خيارات، لذلك وبعد إقصاء الخيارات التي لن يختارها المنافس الثاني يمكن اختصار هذا المخطط وبهذه الطريقة ستتوضح الخطوط التي تعظم أرباح المنافس عند مجموعة معلومات معينة.

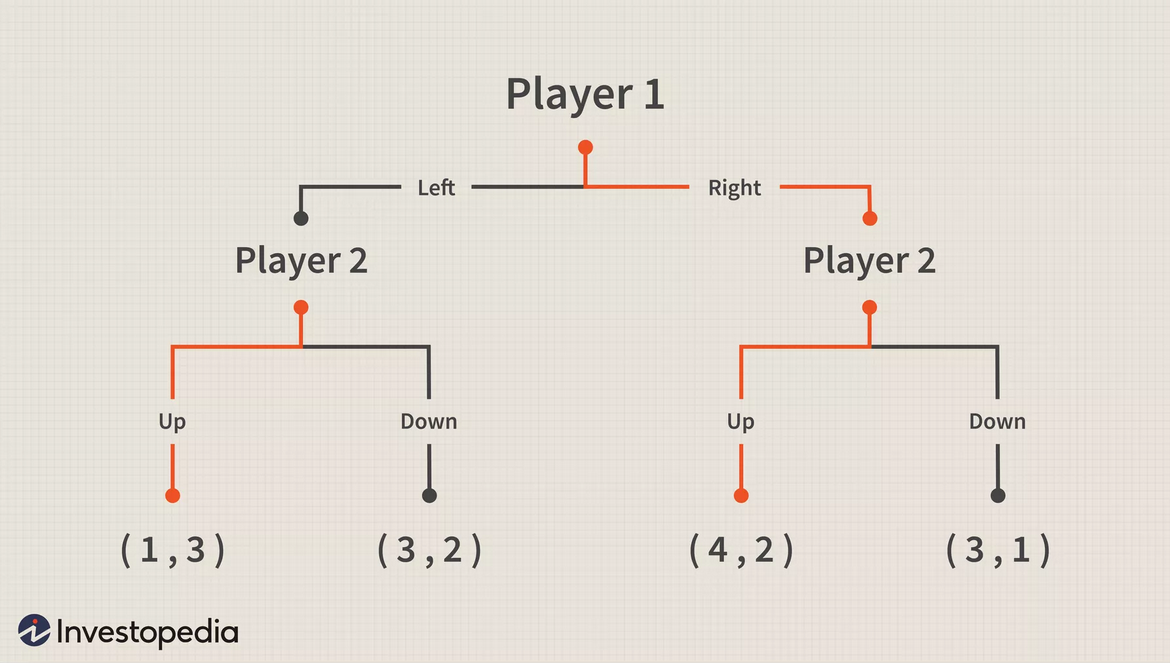
بعد هذا الاختزال يمكن المنافس الأول عند هذه النقطة تعظيم أرباحه بعد معرفة القرارات التي اتخذها المنافس الثاني، توضح هذه النتيجة نقطة تعادل وُجدت بعد استخدام مفهوم الاستقراء الارتجاعي بعد اختيار المنافس الأول لنقطة (اليمين) واختيار المنافس الثاني لنقطة (أعلى)، يوضح المخطط التالي حلًا لهذه اللعبة مع توضيح مسار نقطة التعادل:
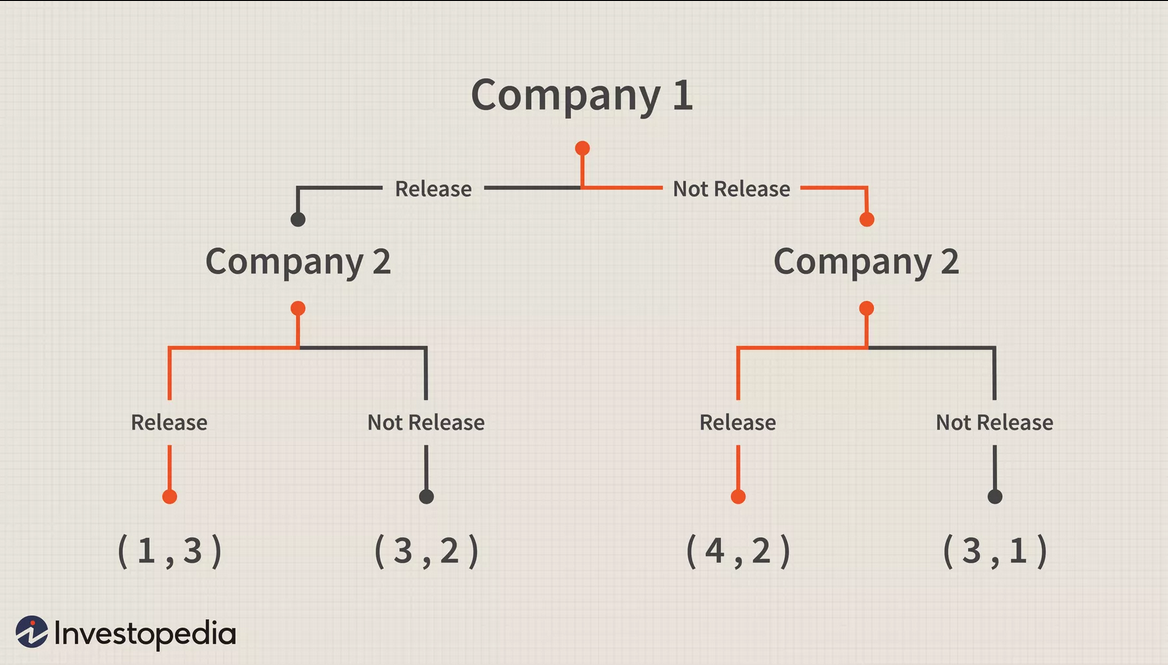
مثالًا على هذه الحالة، يمكن لشخصٍ ما أن يؤسس للعبة مشابهة للحالة الآنفة الذكر عن طريق استخدام شركتين كمنافسين، إذ يمكن لهذه اللعبة أن تتضمن سيناريو طرح منتج جديد، لهذا السبب سيكون السؤال الجدير بالطرح: إذا أرادت الشركة الأولى طرح منتج جديد، ما الاستجابة المحتملة للشركة الثانية؟ هل ستطرح الشركة الثانية منتجًا منافسًا؟
لذلك وبواسطة توقع كمية مبيعات هذا المنتج الجديد ضمن سيناريوهات متعددة يمكننا تمثيل لعبة لتوقع آلية ظهور الأحداث، يوضح المخطط التالي مثالًا لكيفية تمثيل نموذج من هذه الألعاب الرياضية:
أساسيات نظرية الألعاب – التجسيد الفعلي للتفاعل الاستراتيجي بين منافسين أو أكثر ضمن موقف يضم نتائج وقواعد محددة – نظرية الاستراتيجية المثلى
الخلاصة
يمكن إيجاد مجموعة من المخرجات غير الواضحة في موقف حقيقي باستخدام الطرق والمفاهيم البسيطة لنظرية الألعاب، لذلك عند استخدام هذه النظرية للتحليل المالي يصبح من السهل والمفيد حل المشكلات لمواقف حقيقية محتملة مثل حالات اندماج الشركات أو طرح المنتجات الجديدة.
يقدم هذا المقال نظرة تعريفية لنظرية الألعاب ومصطلحاتها الأساسية، إضافةً لطرح أسلوب بسيط لحل الألعاب الرياضية يطلق عليها اصطلاحًا مفهوم الاستقراء الارتجاعي.
مفاهيم متعلقة بنظرية الألعاب الرياضية
يمكن استخدام نظرية الألعاب للمساعدة في تحديد النتائج المرجح حدوثها في الحالات التي تتضمن منافسين أو أكثر مع وجود نتائج ومخرجات معروفة وقابلة للقياس الكمي. فيما يلي تعريفات بعض المصطلحات الشائعة المستخدمة في نظرية الألعاب الرياضية:
- اللعبة: مجموعة الظروف التي تعتمد نتيجتها على أفعال اثنين من صناع القرار أو أكثر.
- المنافس: صانع قرار استراتيجي ضمن سياق اللعبة.
- الاستراتيجية: خطة كاملة من الإجراءات يطبقها المنافس بالنظر للظروف التي يمكن أن تظهر في اللعبة.
- الفائدة/المكافأة: المكسب الذي يتلقاه المنافس عند الوصول إلى نتيجة معينة، يمكن لهذا المكسب أن يأخذ أي شكل كمي من الدولارات إلى المنافع المادية الأخرى.
- مجموعة المعلومات: المعلومات المتوفرة ضمن فترة زمنية معينة. يطبق عادةً مفهوم مجموعة المعلومات عندما يكون للعبة عناصرًا متسلسلة.
- نقطة التعادل/التوازن: النقطة الزمنية التي يصنع فيها المتنافسون القرار مع الوصول إلى نتائج.
من ضمن المفاهيم الاقتصادية الهامة، يعد مصطلح العقلانية والتعظيم من المصطلحات الاقتصادية الهامة لنظرية الألعاب، لهذا السبب يفترض تمتع المنافسين في اللعبة بتفكير عقلاني مع سعيهم لتعظيم مكاسبهم، وعند معاينة الألعاب القائمة يفترض بالنيابة عن المنافس أن تتضمن المكاسب المُدرجة مجموع كافة الأرباح المرتبطة بالنتائج، وهذا الإجراء يقصي كافة الأسئلة من نوع « ماذا لو؟» التي يمكن أن تظهر ضمن عملية اتخاذ القرار.
الجدير بالذكر أنه يمكن نظريًا لعدد اللاعبين أن يكون لا نهائيًا لكن غالبًا ما ينحصر مفهوم معظم الألعاب ضمن سياق التنافس الثنائي، لهذا السبب تعد اللعبة المتسلسلة المؤلفة من متنافسين اثنين واحدة من أبسط الأمثلة على هذه النظرية.
نموذج لحل الألعاب المتسلسلة بالاستقراء الارتجاعي
يمثل المخطط في الصورة أدناه مثالًا بسيطًا للعبة متسلسلة بين منافسين اثنين، فنجد في المقدمة التسميات للمنافس الأول والثاني وضمن هذه التسميات نجد مجموعة المعلومات لكلا المنافسين على التوالي، وتمثل الأرقام ضمن الأقواس في أسفل المخطط النتائج المحققة عند نقطة معينة، الجدير بالذكر أن اللعبة متسلسلة ما يعني أن اللاعب الأول سيتخذ القرار الأول(يسار أو يمين) وبعد ذلك يتخذ اللاعب الثاني القرار (أعلى أوأسفل).

يستخدم مفهوم الاستقراء الارتجاعي مثل جميع مفاهيم نظرية الألعاب مبادئ العقلانية والتعظيم، ما يعني أن المنافس الثاني سيحاول تعظيم مكاسبه في جميع الأحوال الممكنة، ولمجموعتي المعلومات خياران اثنان والمجموع الكلي أربعة خيارات، لذلك وبعد إقصاء الخيارات التي لن يختارها المنافس الثاني يمكن اختصار هذا المخطط وبهذه الطريقة ستتوضح الخطوط التي تعظم أرباح المنافس عند مجموعة معلومات معينة.

بعد هذا الاختزال يمكن المنافس الأول عند هذه النقطة تعظيم أرباحه بعد معرفة القرارات التي اتخذها المنافس الثاني، توضح هذه النتيجة نقطة تعادل وُجدت بعد استخدام مفهوم الاستقراء الارتجاعي بعد اختيار المنافس الأول لنقطة (اليمين) واختيار المنافس الثاني لنقطة (أعلى)، يوضح المخطط التالي حلًا لهذه اللعبة مع توضيح مسار نقطة التعادل:

مثالًا على هذه الحالة، يمكن لشخصٍ ما أن يؤسس للعبة مشابهة للحالة الآنفة الذكر عن طريق استخدام شركتين كمنافسين، إذ يمكن لهذه اللعبة أن تتضمن سيناريو طرح منتج جديد، لهذا السبب سيكون السؤال الجدير بالطرح: إذا أرادت الشركة الأولى طرح منتج جديد، ما الاستجابة المحتملة للشركة الثانية؟ هل ستطرح الشركة الثانية منتجًا منافسًا؟
لذلك وبواسطة توقع كمية مبيعات هذا المنتج الجديد ضمن سيناريوهات متعددة يمكننا تمثيل لعبة لتوقع آلية ظهور الأحداث، يوضح المخطط التالي مثالًا لكيفية تمثيل نموذج من هذه الألعاب الرياضية:

أساسيات نظرية الألعاب – التجسيد الفعلي للتفاعل الاستراتيجي بين منافسين أو أكثر ضمن موقف يضم نتائج وقواعد محددة – نظرية الاستراتيجية المثلى
الخلاصة
يمكن إيجاد مجموعة من المخرجات غير الواضحة في موقف حقيقي باستخدام الطرق والمفاهيم البسيطة لنظرية الألعاب، لذلك عند استخدام هذه النظرية للتحليل المالي يصبح من السهل والمفيد حل المشكلات لمواقف حقيقية محتملة مثل حالات اندماج الشركات أو طرح المنتجات الجديدة.
