تويت
الفاعلية الكيمياوية
الفاعلية الكيمياوية chemical activity (النشاط الكيمياوي) مقدار يستعاض به عن التركيز المولي في قانون فعل الكتلة (قانون لوشاتيليه).
قانون فعل الكتلة
حسب قانون الكتل الفاعلة (وهناك من يسميه قانون فعل الكتلة أو قانون لوشاتيليه)، تُعطى قيمة ثابت التوازن[ر. التوازن الكيمياوي] للتفاعل العكوس:
بالعلاقة:
حيث Kc ثابت التوازن و[C]، [D] تركيز المواد الناتجة من التفاعل، مقدراً كل منها بالمول/لتر و[A]، [B] تركيز المواد الداخلة في التفاعل مقدراً كل منها بالمول/لتر. في المعادلة q هي عدد مولات C، وδ عدد مولات D، وα عدد مولات A، وβ عدد مولات B في معادلة التفاعل، وفي حالة الغازات المثالية يُعطى ثابت التوازن باستخدام الضغوط الجزئية:
والعلاقة بين Kp و Kc يمكن استنتاجها من علاقات ترموديناميكية خاصة بالحالة الغازية المثالية:
حيث R ثابت الغازات الكاملة وT درجة الحرارة المطلقة (كلفن)، وهي تساوي t0 درجة حرارة سلسيوس +273، فيكون التغير في عدد المولات:
أما إذا كانت الجملة غير مثالية، كما في بعض التفاعلات الغازية التي تجري في شروط لا يمكن تطبيق قانون الغازات المثالية عليها، مثل اصطناع غاز النشادر أو الميتانول تحت ضغط عالٍ، أو التفاعلات التي تتم في المحاليل السائلة أو المحاليل الصلبة. ولدراسة مثل هذه الحالات، أي حالات الجمل الحقيقية، كان من الضروري وضع نظرية أعم تتعلق بالتوازنات. والجمل الحقيقية real systems تختلف عن الجمل المثالية في أن الجسيمات المادية في الجمل الحقيقية يتآثر بعضها مع بعض، بعكس الجمل المثالية. لذا، فالقوانين الفيزيائية التي تطبق في حال الجمل المثالية، سواء كانت غازات أم محاليل سائلة أو محاليل صلبة لا تكون صحيحة عند تطبيقها على الجمل الحقيقية.
الكمون الكيمياوي
إن تركيب الجملة التي يجري فيها تفاعل كيمياوي يتغيَّر باستمرار، ولهذا لا يمكن تحديد حالة الجملة بالاقتصار على تعيين الضغط والحجم ودرجة الحرارة. ولدراسة التغيرات الطارئة على تركيب الجملة؛ يجب إدخال متحولات أخرى تقيس كمية كل مكوِّن كيمياوي في الجملة إضافة إلى P وV وT. وقد جرت العادة أن يؤخذ المول للقياس الكيمياوي بالرموز n1 أو n2 أو n3 أو … ni حيث تمثّل قيم n هذه عدد مولات المكوِّن 1 أو 2 أو 3 ... أو i.
وعلى هذا الأساس يكون كل تابع (أو دالة) ترموديناميكي تابعاً لقيم ni كما يتبع درجة الحرارة T والضغط P والحجم V.
فالطاقة الحرة F على سبيل المثال: F = F (P, V, T, ni)، أي إن dF يساوي:
حيث nj هي عدد مولات جميع المكوّنات عدا i.
ومن أجل كل جملة ذات تركيب ثابت يكون: dF = -SdT + VdP[ر. التحريك الحراري] عندما يكون مجموع dni مساوياً الصفر ولهذا:
وعند درجة حرارة ثابتة، وضغط ثابت يكون:
وإن المعامل
وضعه غيبس Gibbs وأطلق عليه اسم الكمون الكيمياويchemical potential P أي إن الكمون الكيمياوي، أو الطاقة الحرة المولية، يُمثِّل تغير الطاقة الحرة الموافق لمول واحد من المادة i بضغط ثابت، ودرجة حرارة ثابتة، وعدد ثابت nj من مولات المكوِّنات الأخرى للجملة عدا i.
وفي حالة الغاز المثالي، يكون الكمون الكيمياوي مساوياً للطاقة الحرة للمول الواحد بضغط قدره Pi وبدءاً من العلاقة:
تنتج العلاقة:
وقيمة μi للغاز المثالي هي نفسها سواء كان الغاز الكامل نقياً ضغطه Pi أم كان في مزيج مؤلف من غازات مثالية وضغطه الجزئي Pi. أما إذا كان المزيج غير مثالي فإن هذا «التطابق» يصبح غير قابل للتطبيق. ويكون هناك قوى تآثر متنوعة متداخلة بعضها مع بعض. ويصبح تقدير μi مسألة تجريبية مستقلة تعيَّن حسب الحالة.
الزوال
إن علاقات مثل العلاقة (10) تؤدي إلى معادلات غاية في البساطة في تطور نظرية التوازن الكيمياوي، ومن المفيد إدخال تابع (أو دالة) جديد يطلق عليه اسم الزوال fugacity، بحيث يبقى شكل المعادلة (10) صحيحاً حتى من أجل الجمل غير المثالية، أي يُكتب:
تدل fi على زوال المادة، fi0 هو زوال المادة في الحالة العيارية. وهنا يجب تغيير تعريف الحالة العيارية فبدلاً من الحالة العيارية (في الحالة المثالية) عندما يكون الضغط مساوياً الضغط الجوي تصبح الحالة العيارية (في الجمل الحقيقية) هي الحالة التي يكون الزوال فيها مساوياً 1، أي:
ويصبح:
ويمكن هنا معالجة التوازن [ر. التوازن الكيميائي] باستعمال الزوال والكمون الكيمياوي. ويتم بذلك الحصول على قيمة ثابت التوازن بصورة عامة وليس في حالة الغازات المثالية فقط، وإنما علاقة عامة صحيحة في جميع الأحوال:
ويمكن حساب الزوال لغاز نقي أو مزيج غازي إذا كانت المعطيات P, V, T متوافرة وهذه الحسابات لا تهم إلا المختصين.
وعندما يقرب الضغط من الصفر، يقترب سلوك الغاز الحقيقي من المثالية، وفي حالة الغاز المثالي يكون الزوال مساوياً الضغط f = P (العلاقة 12).
ومنه ينتج:
ومن العلاقة (15) يمكن حساب قيمة الزوال عند أي ضغط وأي درجة حرارة إذا كانت المعطيات P, V, T معروفة للغاز. فإذا رسم انحراف حجم الغاز الحقيقي عن حجم الغاز المثالي بالشروط نفسها بدلالة P، فيمكن عندها حساب التكامل (15) من المنحني البياني، أو يمكن استعمال معادلة الحالة لحساب a كتابع لـ P، وعندها يمكن حساب التكامل بطريقة تحليلية.
فالزوال يمكن تصوره على أنه «الضغط المثالي» الذي يقيس الميل الحقيقي لهروب الغاز escaping tendency.
ويكون ثابت التوازن:
وبتعويض f بـ γP حيث γ هو معامل الفعالية activity coefficient.
من المعروف أن انحرافات الغازات عن السلوك المثالي تتحدد باقترابها من النقطة الحرجة. وهذا السلوك يتأكد بالحقيقة بأنه في الضغوط الدنيا يكون للغازات جميعها النسبة نفسها
(الشكل-1). وتُدعى هذه النسبة معامل الفعالية 
.
استعمال الزوال لحساب ثوابت التوازن
يمكن بيان هذه الطريقة بأخذ مثال محدد، وليكن التفاعل:
وقد دُرس هذا التفاعل لأهميته الصناعية دراسة مستفيضة، بزيادة ضغط المزيج حتى الألف ضغط جوي. فإذا أخذ مزيج ثلاثة حجوم هدروجين إلى حجم واحد N2 عند درجة حرارة 450 ْس وبضغوط مختلفة تكون النسبة المئوية لـ NH3 في المزيج كما هو مدْرَج في الجدول (1). وفي العمود الثالث في الجدول قيم Kp حيث:
وقد حسبت هذه القيم من المعطيات.
إن قيم Kp للغازات المثالية لا علاقة لها بضغط الغاز، وهذه النتائج (المدرجة في الجدول)، تشير إلى انحرافات شديدة عن المثالية عند الضغوط العالية. حُسبت Kf باستعمال خطوط نيوتن البيانية لحساب الزوال.
يتضح من الجدول (1) أن الغاز يبتعد عن المثالية كلما ازداد ضغطه.
ثوابت التوازن في المحاليل الحقيقية
يعطى الكمون الكيمياوي μ في حالة المحاليل بالعلاقة:
حيث μ الكمون الكيمياوي
μ0 الكمون الكيمياوي العياري
aA فاعلية المكوِّن A في المحلول
حيث
معامل الفعالية، x الكسر الجزيئي
ومعامل الفعالية يبيِّن شدة الانحراف عن المثالية في المحلول. وفي حالة قانون راؤول يكون a = x أو γ = 1.
و
وإن الفعالية هي نسبة الزوال إلى الزوال في الحالة العيارية. وإن الحالة العيارية هي انتقائية.
وإن ثابت التوازن للتفاعل (في المحلول):
وفي المحلول المثالي، تكون معاملات الفعالية مساوية الوحدة، ويكون ثابت التوازن هو Kx. ولا يوجد معطيات كافية عن معاملات الفعالية في المحاليل غير الإلكتروليتية، وإن التطبيق الفعلي ذا الأهمية لتابع الفعالية يفيد في دراسة المحاليل الكهرليتية (الكهارل) بخاصة.
وفي الحالة المعيارية للمنحل في محلول تكون الفعالية مساوية 1. وبما أن المحاليل الممددة جداً تسلك السلوك المثالي، فإن a تقترب من m (أو c) ولهذا تقترب γ (أو f) من 1 في هذه المحاليل. ويبيّن الجدول (2) تغير معامل الفعالية لمحلول كهرليتي ولمحلول غير كهرليتي بالتمديد.
ويمكن حساب معامل فعالية أيون في المحاليل المائية للكهرليتات بوساطة عبارة ديباي-هيوكل التي تستخدم القوة الأيونية في الشرطين العياريين (من أجل قيم غير كبيرة للقوة الأيونية).
I القوة الأيونية التي تحسب من العلاقة العامة:
حيث ci التركيز المولي للأيون وzi شحنة الأيون، والمعامل γi هو الذي يحدد انحراف خواص المحلول الحقيقية عن خواص الحالة المثاليّة (حيث يساوي الواحدة فيها).
وليد البزرة
الفاعلية الكيمياوية chemical activity (النشاط الكيمياوي) مقدار يستعاض به عن التركيز المولي في قانون فعل الكتلة (قانون لوشاتيليه).
قانون فعل الكتلة
حسب قانون الكتل الفاعلة (وهناك من يسميه قانون فعل الكتلة أو قانون لوشاتيليه)، تُعطى قيمة ثابت التوازن[ر. التوازن الكيمياوي] للتفاعل العكوس:
بالعلاقة:
حيث Kc ثابت التوازن و[C]، [D] تركيز المواد الناتجة من التفاعل، مقدراً كل منها بالمول/لتر و[A]، [B] تركيز المواد الداخلة في التفاعل مقدراً كل منها بالمول/لتر. في المعادلة q هي عدد مولات C، وδ عدد مولات D، وα عدد مولات A، وβ عدد مولات B في معادلة التفاعل، وفي حالة الغازات المثالية يُعطى ثابت التوازن باستخدام الضغوط الجزئية:
والعلاقة بين Kp و Kc يمكن استنتاجها من علاقات ترموديناميكية خاصة بالحالة الغازية المثالية:
حيث R ثابت الغازات الكاملة وT درجة الحرارة المطلقة (كلفن)، وهي تساوي t0 درجة حرارة سلسيوس +273، فيكون التغير في عدد المولات:
أما إذا كانت الجملة غير مثالية، كما في بعض التفاعلات الغازية التي تجري في شروط لا يمكن تطبيق قانون الغازات المثالية عليها، مثل اصطناع غاز النشادر أو الميتانول تحت ضغط عالٍ، أو التفاعلات التي تتم في المحاليل السائلة أو المحاليل الصلبة. ولدراسة مثل هذه الحالات، أي حالات الجمل الحقيقية، كان من الضروري وضع نظرية أعم تتعلق بالتوازنات. والجمل الحقيقية real systems تختلف عن الجمل المثالية في أن الجسيمات المادية في الجمل الحقيقية يتآثر بعضها مع بعض، بعكس الجمل المثالية. لذا، فالقوانين الفيزيائية التي تطبق في حال الجمل المثالية، سواء كانت غازات أم محاليل سائلة أو محاليل صلبة لا تكون صحيحة عند تطبيقها على الجمل الحقيقية.
الكمون الكيمياوي
إن تركيب الجملة التي يجري فيها تفاعل كيمياوي يتغيَّر باستمرار، ولهذا لا يمكن تحديد حالة الجملة بالاقتصار على تعيين الضغط والحجم ودرجة الحرارة. ولدراسة التغيرات الطارئة على تركيب الجملة؛ يجب إدخال متحولات أخرى تقيس كمية كل مكوِّن كيمياوي في الجملة إضافة إلى P وV وT. وقد جرت العادة أن يؤخذ المول للقياس الكيمياوي بالرموز n1 أو n2 أو n3 أو … ni حيث تمثّل قيم n هذه عدد مولات المكوِّن 1 أو 2 أو 3 ... أو i.
وعلى هذا الأساس يكون كل تابع (أو دالة) ترموديناميكي تابعاً لقيم ni كما يتبع درجة الحرارة T والضغط P والحجم V.
فالطاقة الحرة F على سبيل المثال: F = F (P, V, T, ni)، أي إن dF يساوي:
حيث nj هي عدد مولات جميع المكوّنات عدا i.
ومن أجل كل جملة ذات تركيب ثابت يكون: dF = -SdT + VdP[ر. التحريك الحراري] عندما يكون مجموع dni مساوياً الصفر ولهذا:
وعند درجة حرارة ثابتة، وضغط ثابت يكون:
وإن المعامل
وضعه غيبس Gibbs وأطلق عليه اسم الكمون الكيمياويchemical potential P أي إن الكمون الكيمياوي، أو الطاقة الحرة المولية، يُمثِّل تغير الطاقة الحرة الموافق لمول واحد من المادة i بضغط ثابت، ودرجة حرارة ثابتة، وعدد ثابت nj من مولات المكوِّنات الأخرى للجملة عدا i.وفي حالة الغاز المثالي، يكون الكمون الكيمياوي مساوياً للطاقة الحرة للمول الواحد بضغط قدره Pi وبدءاً من العلاقة:
تنتج العلاقة:
وقيمة μi للغاز المثالي هي نفسها سواء كان الغاز الكامل نقياً ضغطه Pi أم كان في مزيج مؤلف من غازات مثالية وضغطه الجزئي Pi. أما إذا كان المزيج غير مثالي فإن هذا «التطابق» يصبح غير قابل للتطبيق. ويكون هناك قوى تآثر متنوعة متداخلة بعضها مع بعض. ويصبح تقدير μi مسألة تجريبية مستقلة تعيَّن حسب الحالة.
الزوال
إن علاقات مثل العلاقة (10) تؤدي إلى معادلات غاية في البساطة في تطور نظرية التوازن الكيمياوي، ومن المفيد إدخال تابع (أو دالة) جديد يطلق عليه اسم الزوال fugacity، بحيث يبقى شكل المعادلة (10) صحيحاً حتى من أجل الجمل غير المثالية، أي يُكتب:
تدل fi على زوال المادة، fi0 هو زوال المادة في الحالة العيارية. وهنا يجب تغيير تعريف الحالة العيارية فبدلاً من الحالة العيارية (في الحالة المثالية) عندما يكون الضغط مساوياً الضغط الجوي تصبح الحالة العيارية (في الجمل الحقيقية) هي الحالة التي يكون الزوال فيها مساوياً 1، أي:
ويصبح:
ويمكن هنا معالجة التوازن [ر. التوازن الكيميائي] باستعمال الزوال والكمون الكيمياوي. ويتم بذلك الحصول على قيمة ثابت التوازن بصورة عامة وليس في حالة الغازات المثالية فقط، وإنما علاقة عامة صحيحة في جميع الأحوال:
ويمكن حساب الزوال لغاز نقي أو مزيج غازي إذا كانت المعطيات P, V, T متوافرة وهذه الحسابات لا تهم إلا المختصين.
وعندما يقرب الضغط من الصفر، يقترب سلوك الغاز الحقيقي من المثالية، وفي حالة الغاز المثالي يكون الزوال مساوياً الضغط f = P (العلاقة 12).
ومنه ينتج:
ومن العلاقة (15) يمكن حساب قيمة الزوال عند أي ضغط وأي درجة حرارة إذا كانت المعطيات P, V, T معروفة للغاز. فإذا رسم انحراف حجم الغاز الحقيقي عن حجم الغاز المثالي بالشروط نفسها بدلالة P، فيمكن عندها حساب التكامل (15) من المنحني البياني، أو يمكن استعمال معادلة الحالة لحساب a كتابع لـ P، وعندها يمكن حساب التكامل بطريقة تحليلية.
فالزوال يمكن تصوره على أنه «الضغط المثالي» الذي يقيس الميل الحقيقي لهروب الغاز escaping tendency.
ويكون ثابت التوازن:
وبتعويض f بـ γP حيث γ هو معامل الفعالية activity coefficient.
من المعروف أن انحرافات الغازات عن السلوك المثالي تتحدد باقترابها من النقطة الحرجة. وهذا السلوك يتأكد بالحقيقة بأنه في الضغوط الدنيا يكون للغازات جميعها النسبة نفسها
(الشكل-1). وتُدعى هذه النسبة معامل الفعالية .  |
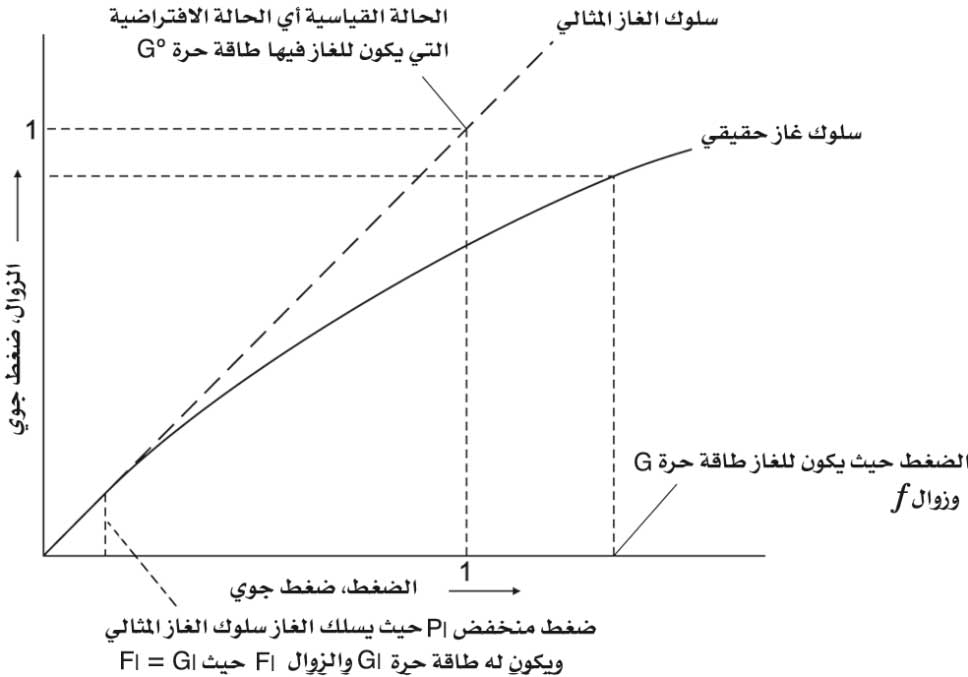| الشكل (1) تمثيل تخطيطي للعلاقة زوال - ضغط لغاز حقيقي، ولغاز مثالي حتى الضغط (1) جو |
يمكن بيان هذه الطريقة بأخذ مثال محدد، وليكن التفاعل:
وقد دُرس هذا التفاعل لأهميته الصناعية دراسة مستفيضة، بزيادة ضغط المزيج حتى الألف ضغط جوي. فإذا أخذ مزيج ثلاثة حجوم هدروجين إلى حجم واحد N2 عند درجة حرارة 450 ْس وبضغوط مختلفة تكون النسبة المئوية لـ NH3 في المزيج كما هو مدْرَج في الجدول (1). وفي العمود الثالث في الجدول قيم Kp حيث:
وقد حسبت هذه القيم من المعطيات.
إن قيم Kp للغازات المثالية لا علاقة لها بضغط الغاز، وهذه النتائج (المدرجة في الجدول)، تشير إلى انحرافات شديدة عن المثالية عند الضغوط العالية. حُسبت Kf باستعمال خطوط نيوتن البيانية لحساب الزوال.
| الضغط الكلي (جو) | النسبة المئوية لـ NH3 عند التوازن | KP | Kγ | Kf |
| 10 | 2.04 | 0.00659 | 0.995 | 0.00655 |
| 30 | 5.80 | 0.00676 | 0.975 | 0.00659 |
| 50 | 9.17 | 0.00690 | 0.945 | 0.00650 |
| 100 | 16.36 | 0.00725 | 0.880 | 0.00636 |
| 300 | 35.5 | 0.00884 | 0.688 | 0.00608 |
| 600 | 53.6 | 0.01294 | 0.497 | 0.0642 |
| 1000 | 69.4 | 0.04328 | 0.343 | 0.01010 |
| الجدول (1) التوازن في اصطناع النشادر عند درجة حرارة 450 ْس، النسبة بين H2 وN2 تساوي 3/1 | ||||
ثوابت التوازن في المحاليل الحقيقية
يعطى الكمون الكيمياوي μ في حالة المحاليل بالعلاقة:
حيث μ الكمون الكيمياوي
μ0 الكمون الكيمياوي العياري
aA فاعلية المكوِّن A في المحلول
حيث
معامل الفعالية، x الكسر الجزيئيومعامل الفعالية يبيِّن شدة الانحراف عن المثالية في المحلول. وفي حالة قانون راؤول يكون a = x أو γ = 1.
و
وإن الفعالية هي نسبة الزوال إلى الزوال في الحالة العيارية. وإن الحالة العيارية هي انتقائية.
وإن ثابت التوازن للتفاعل (في المحلول):
وفي المحلول المثالي، تكون معاملات الفعالية مساوية الوحدة، ويكون ثابت التوازن هو Kx. ولا يوجد معطيات كافية عن معاملات الفعالية في المحاليل غير الإلكتروليتية، وإن التطبيق الفعلي ذا الأهمية لتابع الفعالية يفيد في دراسة المحاليل الكهرليتية (الكهارل) بخاصة.
وفي الحالة المعيارية للمنحل في محلول تكون الفعالية مساوية 1. وبما أن المحاليل الممددة جداً تسلك السلوك المثالي، فإن a تقترب من m (أو c) ولهذا تقترب γ (أو f) من 1 في هذه المحاليل. ويبيّن الجدول (2) تغير معامل الفعالية لمحلول كهرليتي ولمحلول غير كهرليتي بالتمديد.
| m (مول/كغ) | g من أجل الغليسرول | g من أجل NaCl |
| 0 | 1.00 | 1.00 |
| 0.005 | .... | 0.930 |
| 0.1 | 1.006 | 0.778 |
| 0.5 | 1.032 | 0.679 |
| 1.0 | 1.068 | 0.656 |
| 2.0 | 1.132 | 0.670 |
| 3.0 | .... | 0.719 |
| 5.0 | 1.348 | ... |
| الجدول (2) تغير معامل الفعالية بتغير m التركيز المولي الوزني في الماء حيث m التركيز المولي الوزني: هو عدد المولات في 1000غ محلول |
||
I القوة الأيونية التي تحسب من العلاقة العامة:
حيث ci التركيز المولي للأيون وzi شحنة الأيون، والمعامل γi هو الذي يحدد انحراف خواص المحلول الحقيقية عن خواص الحالة المثاليّة (حيث يساوي الواحدة فيها).
وليد البزرة