اشعاع حراري
Thermal radiation - Radiation thermique
الإشعاع الحراري
الإشعاع الحراري thermal radiation إصدار تلقائي لإشعاعات كهرمغنطيسية تصدرها الأجسام وتتوقف شدتها على درجة حرارتها. وهي إشعاعات تحمل طاقة وتصدرها الأجسام مهما كانت درجة حرارتها في مجالٍ ما من الأطوال الموجية، وتكون شدتها عظمى عند طولٍ موجي متوسط في هذا المجال تتوقف قيمته على طبيعة الجسم وعلى درجة حرارته.
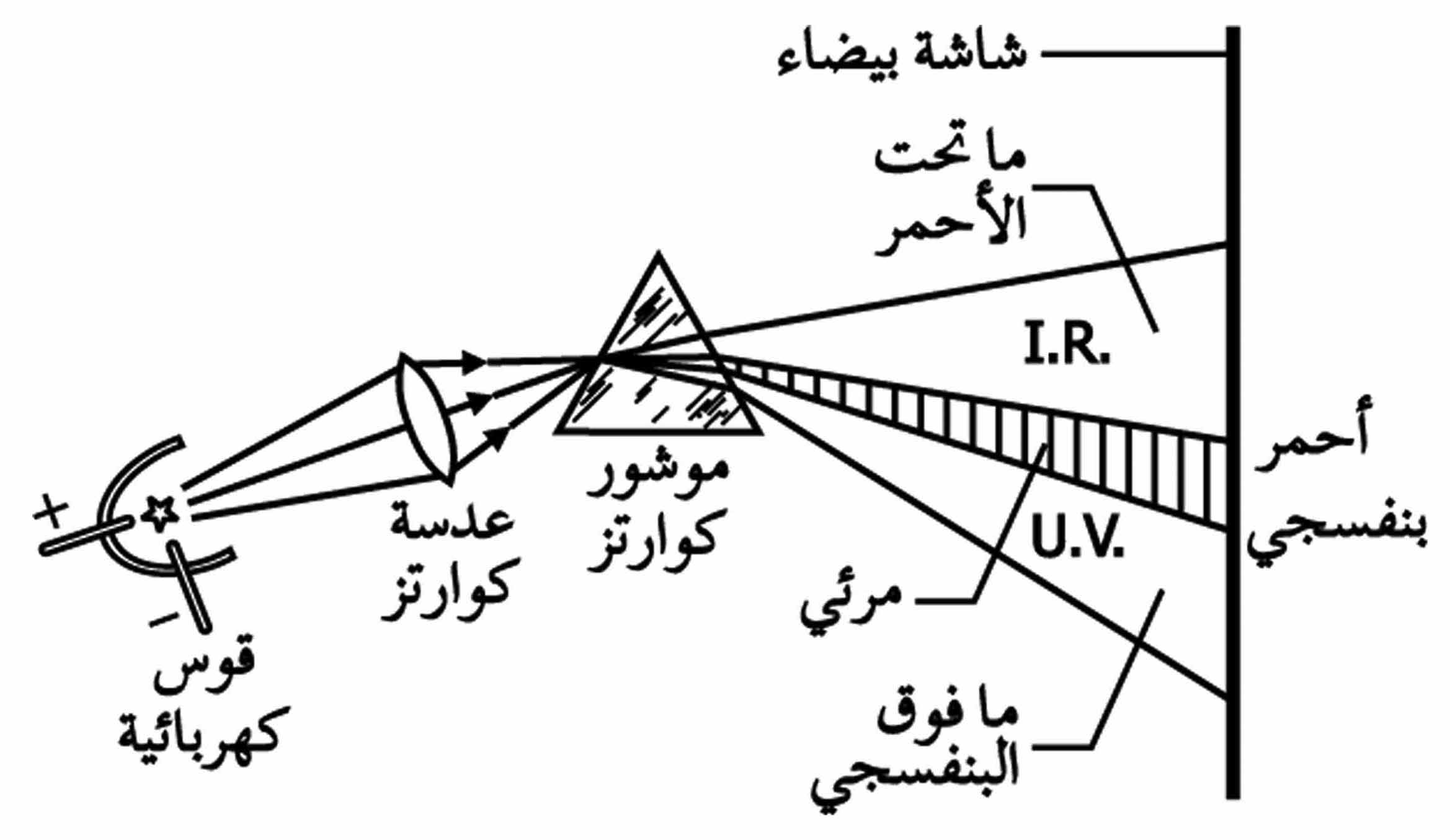 |
| الشكل (1) التحليل الطيفي للإشعاع الصادر عن منبع حار كالقوس الكهربائية |
وإذا تعرض جسمٌ ما لإشعاع حراري صادر عن جسم آخر فإنه يعكس جزءاً من هذا الإشعاع ويمتص الجزء الباقي إذا كان عاتماً مما يؤدي إلى رفع درجة حرارته، فيزداد إشعاعه الحراري الذاتي، فإذا تساوى ما يتلقاه الجسم من إشعاع حراري مع ما يصدره من هذا الإشعاع بلغ الجسم حالة التوازن الحراري.
 |
| الشكل (2) الجسم الماص المثالي أو الجسم الأسود |
الإشعاع الحراري للجسم الأسود
لقد بينت الدراسة التجريبية للإشعاع الصادر عن الأجسام الصلبة الحارة بالأسلوب المبين في الشكل 1 أن الإشعاع مستقل عن طبيعة المادة التي يُصنع منها الجسم الأسود، وأن توزع شدته يتبع طول الموجة λ إضافة إلى درجة حرارة الجسم الأسود، ويبين الشكل 3 نتائج نموذجية عائدة لأجسام صلبة ماصة مثالية في درجات حرارة مختلفة مقدرة في سلم كلفن. وهو يعطي الاستطاعة الوحيدة اللون «Pλ» monochromatic power التي تصدرها واحدة السطح من جسم أسود بدلالة λ. ويمكن الحصول على الاستطاعة الكلية P بإجراء عملية تكامل على مدى الأطوال الموجية جميعها، أي من العلاقة:
 |
 |
| الشكل (3) الاستطاعة الصادرة عن الجسم الأسود الحار في درجات حرارة مختلفة وبتغير الطول الموجي λ |
| (1) |  |
 |
قانون فين في الإشعاع: بحث فين Wien في المعادلة الرياضية التي تعطي Pλ بدلالة كل من درجة حرارة الجسم الأسود T وطول موجة الإشعاع λ، وقادته محاولته هذه إلى المعادلة التالية:
| (2) |  |
 |
| الشكل (4) تبين المقارنة قانون فين في الإشعاع وقتنون رايلي وجينز مع النتائج التجريبية لإشعاع الجسم الأسود في درجة حرارة محددة |
c2 = 1.439 × 10-2 m. k
ويبين الشكل 4 منحني قانون فين في الإشعاع مع المنحني التجريبي ويظهر فيه أنه ينطبق على المنحني التجريبي في الأطوال الموجية الصغيرة، ويختلف عنه في الأطوال الموجية الكبيرة. وتجدر الإشارة إلى أن معادلة فين هذه لا تستند إلى أسس نظرية.
قانون رايلي وجينز: أدت المحاولة النظرية لرايلي وجينز Rayleigh- Jeans التي اعتمدت على أسس فيزيائية تقليدية إلى معادلة تعطي Pλ بدلالة λ وT وتنسجم انسجاماً جيداً مع القيم التجريبية عند قيم λ الكبيرة، كما يتضح ذلك في الشكل 4، إلا أن المنحني التجريبي ينتهي إلى اللانهاية عند قيم λ الصغيرة، وهو ما اصطلح عليه باسم الكارثة فوق البنفسجية، ذلك أن تباعد المنحني إلى اللانهاية عند λ المقابلة للإشعاع فوق البنفسجي دلّ على وجود خلل جذري في النظرية التقليدية التي اعتمد عليها كل من رايلي وجينز في استنتاج قانونهما من منطلقات تبادل الطاقة بين المادة والإشعاع. وينص قانون رايلي وجينز على أن:
Pλ = 2πckTλ-4
حيث:
k = 1.381× 10-23 J.K-1
ويعرف باسم ثابت بولتزمان وc سرعة الضوء في الخلاء، ويصلح هنا القانون عندما يكون الجداء λT أكبر من 0.7 متر كلفن.
قانون بلانك: وهو يعتمد على فرضية الكم (الكوانتا) التي تنص على أن الإشعاع يصدر عن المادة بصورة كمّات أو فوتونات يحمل كل منها طاقة تتناسب مع تردد الإشعاع الصادر، وتُعطى بجداء التردد بثابت بلانك(h) Planck لقد أدت هذه الفرضية الجريئة إلى معادلة لـPλ تتفق اتفاقاً تاماً مع النتائج التجريبية من أجل جميع قيم λ. أما صيغة قانون بلانك التي اكتشفها عام 1900 والتي عُدت إحدى منجزات ميكانيك الكم [ر] المهمة فهي:
 |
c1 = 2hc2 = 3.74150 × 10-16 w.m2
و: ْc2 = hc/k = 1.43879 × 10-2 m. k
تمثل c هنا سرعة الضوء في الخلاء و k ثابت بولتزمان وh ثابت بلانك الذي تساوي قيمته العددية:
h = 6.626 × 10-34 J.sec
ويمكن البرهان بسهولة على أن كلاً من قانون فين وقانون رايلي وجينز ما هو إلا حالة خاصة من قانون بلانك عند λ القصيرة (فين) أو λ الطويلة (رايلي وجينز).
قانون فين في الانزياح: لاحظ فين أن النهاية العظمى لمنحني Pλ في الشكل ـ4 تنزاح نحو الأطوال الموجية القصيرة بارتفاع درجة حرارة الجسم الأسود، بمعنى أن λmax تتناسب عكسياً مع درجة الحرارة T، أي:
.kْ ْ2.898 ×107 A = ثابت = λmax.T
حيث تقدَّر λ بالأنغستروم Aْ وT بالدرجة كلفن K.
الإشعاع الحراري للأجسام غير السوداء
يخضع هذا الإشعاع الحراري إلى قانون كيرشوف G.Kirchhoff، وهو ينص على أن معدل الإشعاع الحراري الكلي لجسم ما أو امتصاصه لا يتعلق بدرجة حرارته المطلقة فحسب، كما هو الحال في الجسم الأسود، وإنما يرتبط أيضاً بطبيعة سطحه، وهو في جميع الأحوال أدنى من معدّل الإشعاع الحراري الكلي للجسم الأسود. ويمكن التعبير رياضياً عن هذا القانون بالعلاقة:
 |
 |
| الشكل (5) الاستطاعة الإشعاعية الوحيدةاللون لجسم غير أسود مقارنة باستطاعة الجسم الأسود |
إن المنحني Pλ بدلالة λ للأجسام غير السوداء يقع تحت المنحني المماثل العائد للجسم الأسود، ويظهر في الشكل (5) منحن يعود لجسم غير أسود مصنوع من خليطة أوي Auer المؤلفة من السيريوم والحديد وبعض المعادن النادرة والمستخدمة كأحجار قداحة. ويبدو فيه واضحاً أن المنحني Pλ يقع دوماً تحت المنحني العائد للجسم الأسود، وبالتالي فإن P الكلية هي أقل مما يقابلها في الجسم الأسود.
تطبيقات الإشعاع الحراري
من تطبيقات الإشعاع الحراري قياس درجات الحرارة العالية باستعمال مقياس النار[ر] (البيرومتر) pyrometer وهو مقياس يقارن شدة الإشعاع الحراري للجسم الحار مع شدة إشعاع منبع حراري معروف، فهو إذن يقيس درجة حرارة الجسم الحار من بُعد من دون أن يمسه.
هناك أنواع مختلفة من مقاييس النار، فالمقياس ذو السلك الخفيّ يعتمد في قياسه على قانون فين في الإشعاع الحراري (العلاقة 2) الذي يعطي:
 |
 |
أحمد حصري
