معادلات تفاضليه عاديه
Ordinary differential equations - Equations différentielles ordinaires
المعادلات التفاضلية العادية
المعادلة التفاضلية differential equationهي علاقة تربط بين متحول (متغير) مستقل واحد أو أكثر والدالة function المبحوث عنها التابعة لهذه المتحولات (التي يفترض أنها وحيدة التعيين) ومشتقات هذه الدالَّة بالنسبة لهذه المتحولات، التي يفترض أنها متحولات حقيقية وكذلك الدالة.
مثال (1): المعادلة التفاضلية xy/ + 2y = x2 +1 تربط بين الدالة y ومشتقها y والمتحول المستقل x.
ظهر مفهوم المعادلات التفاضلية منذ طرح مفهوم التفاضل، وبدأ يتعزز على نحو أقوى مع بداية القرن السادس عشر. وتطورت موضوعات المعادلات التفاضلية بسرعة، لكثرة تطبيقاتها وارتباطها المباشر بعدد من فروع الرياضيات مثل الحساب التفاضلي والتكاملي والمعادلات التكاملية وحساب التغيرات ومسائل التقريب والحلول المثلى والشروط الحدِّية وكثير من البحوث الفيزيائية والميكانيكية والكيمياوية.
عندما تكون الدالة متعلقة بمتغير واحد فالمعادلة التفاضلية تمثل معادلة تفاضلية عادية ordinary differential equation، أما عندما تكون الدالة متعلقة بعدد من المتغيرات فالمعادلة تدعى معادلة تفاضلية جزئية partial differential equation. وكما في المعادلات الجبرية فهناك جملة معادلات تفاضلية عادية، وكذلك جملة معادلات تفاضلية جزئية.
مرتبة المعادلة التفاضلية ودرجتها
مرتبة order المعادلة التفاضلية العادية تحددها أكبر مرتبة مشتق تحويه المعادلة التفاضلية، أما درجتها degree فتحددها أكبر قوة لأعلى المشتقات مرتبة.
في حالة دالة وحيدة مجهولة y ومتحول واحد x فإن المعادلة التفاضلية العادية التي تربط بين المتغير x والدالة المجهولة المتعلقة بهذا المتحول y = y (x) ومشتقات هذه الدالة y/, y//, …, y(n) يكون لها الشكل F (x, y, y/, y//, …, y(n) ) = 0.
وعندما يمكن كتابة المعادلة التفاضلية السابقة كمعادلة محلولة بالنسبة لأعلى المشتقات مرتبة فيصبح y(n) = f (x, y, y/, y//, …, y(n – 1)).
المعادلة التفاضلية الخطية linear differential equation
مثال (2): المعادلة y// - x2 y/ + 2 y2 = x3
معادلة تفاضلية من المرتبة الثانية والدرجة الأولى.
عندما يكون للمعادلة السابقة الشكل
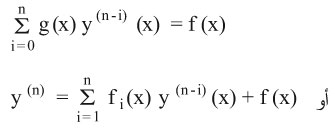
حيث: y(0) (x) = y (x)
فإنها تدعى معادلة خطية من المرتبة n، والمعادلة
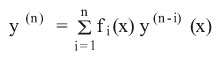
تدعى معادلة خطية متجانسة من المرتبة n، أو يقال إنها معادلة تفاضلية خطية من المرتبة n من دون طرف ثانٍ.
أما المعادلة التفاضلية
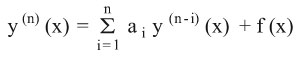
فتدعى معادلة تفاضلية خطية من المرتبة n ذات أمثال ثابتة.
والمعادلة
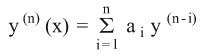
تدعى معادلة تفاضلية خطية متجانسة من المرتبة n ذات أمثال ثابتة. والمعاملات الثوابت a1, a2, …, an هي أعداد حقيقية.
مثال (3): المعادلة y// - 7 y/ + 10 y = sin x معادلة تفاضلية من المرتبة الثانية ذات أمثال ثابتة.
حل معادلة تفاضلية
تكون الدالة y = g (x) حلاً للمعادلة التفاضلية العادية إذا كانت المشتقات المتتالية y/ = g / (x), y// = g// (x), …, y (n) = g(n) (x) موجودة، وتبديلها في المعادلة التفاضلية يحوِّل المعادلة إلى مطابقة. وفي بعض الأحيان قد يعطى الحل بشكل دالة ضمنية F (x, y) = 0 أو بالشكل الوسيطي x = x (t), y = y (t)
وعملية إيجاد الحل لمعادلة تفاضلية تسمى مكاملة هذه المعادلة وهي مسألة معاكسة للحساب التفاضلي، والحل العام general solution للمعادلة التفاضلية من المرتبة n يجب أن يحوي n ثابتاً اختيارياً.
وقد يكون هذا الحل من الشكل الديكارتي y = g (x, c1 , c2 , …, cn) أو من الشكل الوسيطي x = x (t, c1 , c2 , …, cn), y = y (t, c1 , c2 , …, cn) أو من الشكل الضمني F (x, y, c1 , c2 , …, cn) = 0.
ومسألة إيجاد حل للمعادلة التفاضلية يحقق هو ومشتقاته شروطاً إضافية معطاة هي من المسائل المهمة التي تندرج تحت اسم مسألة الشروط الابتدائية initial conditions أو مسألة كوشي Cauchy، وعادة هذه الشروط تعطى بالشكل
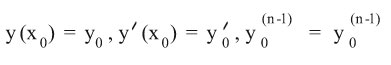
وهندسياً فإن هذا يعني إيجاد منحن تكاملي y = y (x) يمر من النقطة M (x0 , y0) ويحقق الشروط التي ربما ترتبط بخواص هندسية للحصول على أحد منحنيات الأسرة التي تشكل الحل العام. والذي يدعى بالحل الخاص special solution.
ولإيجاد الحل العام للمعادلة التفاضلية الخطية بأمثال حقيقية ثابتة من المرتبة n ذات الشكل:
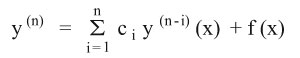
يتم البحث عن جذور المعادلة المميزة لها والتي لها الشكل:
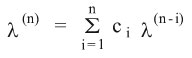
والتي يتم الحصول عليها بتبديل y (n) بالحد λn. وللجذور الحالات الآتية:
أ) الجذور كلها حقيقية ولتكن λ1, λ2, …, λn والحل العام للمعادلة المتجانسة هو
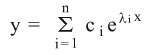
حيث yi = ci e ix (1 ≤ i ≤ n) حلول خاصة وci (1 ≤ i ≤ n) ثوابت كيفية.
مثال (4): المعادلة المميزة للمعادلة التفاضلية المتجانسةy// - y/ - 2y = 0 هي λ2 - λ - 2 = 0 جذراها λ1 = -1 وλ2 = 2 وحلها العام y = c1e-x + c2e2x
ب) بعض الجذور حقيقية والحل الموافق لها كما سبق في المثال (4). وأخرى عقدية مترافقة λm = αm ± i βm والحل الموافق لجذرين مترافقين هو amx (cmcos βmx + c/m sin βmx)
حيثc/m cm ثابتان كيفيان حقيقيان. والحل الخاص للمعادلة هو كل حل يحققها.
هذا وإن الحل العام للمعادلة الخطية غير المتجانسة هو مجموع حلين الأول حل عام لمتجانستها، والآخر هو حل خاص لغير المتجانسة.
بعض أنواع المعادلات التفاضلية العادية من المرتبة الأولى
أ) إن أبسط أنواع المعادلات التفاضلية العادية هي ذات الشكل:

فالمسألة تؤول لحساب تكامل الطرف الأيمن.
ب) إن المعادلة M (x, y) dx + N (x, y) dy = 0 تسمى ذات متحولات قابلة للفصل إذا أمكن ردها للشكل j (x) dx +g ( y) dy = 0 وحلها يعطى بالعلاقة ∫j (x) dx + ∫ g (y) dy = C، حيث C ثابت كيفي.
ج) المعادلة M (x, y) dx + N (x, y) dy = 0 تسمى متجانسة إذا كان تابعاها M (x, y), N (x, y) متجانسين ومن مرتبة التجانس نفسها أي إذا كان M (tx, ty) = tm M (x, y) وN (tx, ty) = tm N (x, y) أو بشكل آخر إذا أمكن كتابتها بالشكل
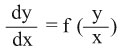
ولحلها يجرى التبديل y = zx ومنه dy = zdx + xdz لترد بعد التبديل إلى معادلة تفاضلية قابلة للفصل.
د)
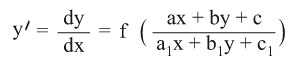
حيث (a, b, c, a1, b1, c1) ثوابت ترد لمعادلة متجانسة.
هـ) المعادلة التفاضلية y/ + p (x) y = q (x) تدعى معادلة خطية من المرتبة الأولى وحلها بالشكل y = e- ∫ p (x) dx [C + ∫ q (x)e ∫ p (x) dx dx] حيث C ثابت كيفي.
و) المعادلة التفاضلية y/ + p (x) y = q (x) y// تدعى معادلة برنولي Bernoulli وهي ترد لمعادلة تفاضلية خطية بالتبديل z = y1 - n وdz = (1 - n) y-n dy وتحل عندها كمعادلة خطية.
ز) المعادلة y/ = p (x) y2 + q (x) y + r (x) وتدعى معادلة ريكاتي Riccati، ومعرفة حل خاص لها y = y1 يسهل حلها بإجراء التبديل
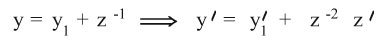
الذي يردها لمعادلة خطية.
ح) المعادلة M (x, y) dx + N (x, y) dy = 0 تكون معادلة تامة إذا حققت العلاقة
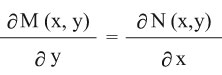
وحلها له الشكل
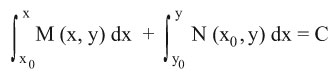
أو
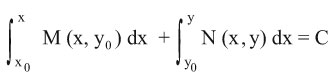
محيي الدين بحبوح
Ordinary differential equations - Equations différentielles ordinaires
المعادلات التفاضلية العادية
المعادلة التفاضلية differential equationهي علاقة تربط بين متحول (متغير) مستقل واحد أو أكثر والدالة function المبحوث عنها التابعة لهذه المتحولات (التي يفترض أنها وحيدة التعيين) ومشتقات هذه الدالَّة بالنسبة لهذه المتحولات، التي يفترض أنها متحولات حقيقية وكذلك الدالة.
مثال (1): المعادلة التفاضلية xy/ + 2y = x2 +1 تربط بين الدالة y ومشتقها y والمتحول المستقل x.
ظهر مفهوم المعادلات التفاضلية منذ طرح مفهوم التفاضل، وبدأ يتعزز على نحو أقوى مع بداية القرن السادس عشر. وتطورت موضوعات المعادلات التفاضلية بسرعة، لكثرة تطبيقاتها وارتباطها المباشر بعدد من فروع الرياضيات مثل الحساب التفاضلي والتكاملي والمعادلات التكاملية وحساب التغيرات ومسائل التقريب والحلول المثلى والشروط الحدِّية وكثير من البحوث الفيزيائية والميكانيكية والكيمياوية.
عندما تكون الدالة متعلقة بمتغير واحد فالمعادلة التفاضلية تمثل معادلة تفاضلية عادية ordinary differential equation، أما عندما تكون الدالة متعلقة بعدد من المتغيرات فالمعادلة تدعى معادلة تفاضلية جزئية partial differential equation. وكما في المعادلات الجبرية فهناك جملة معادلات تفاضلية عادية، وكذلك جملة معادلات تفاضلية جزئية.
مرتبة المعادلة التفاضلية ودرجتها
مرتبة order المعادلة التفاضلية العادية تحددها أكبر مرتبة مشتق تحويه المعادلة التفاضلية، أما درجتها degree فتحددها أكبر قوة لأعلى المشتقات مرتبة.
في حالة دالة وحيدة مجهولة y ومتحول واحد x فإن المعادلة التفاضلية العادية التي تربط بين المتغير x والدالة المجهولة المتعلقة بهذا المتحول y = y (x) ومشتقات هذه الدالة y/, y//, …, y(n) يكون لها الشكل F (x, y, y/, y//, …, y(n) ) = 0.
وعندما يمكن كتابة المعادلة التفاضلية السابقة كمعادلة محلولة بالنسبة لأعلى المشتقات مرتبة فيصبح y(n) = f (x, y, y/, y//, …, y(n – 1)).
المعادلة التفاضلية الخطية linear differential equation
مثال (2): المعادلة y// - x2 y/ + 2 y2 = x3
معادلة تفاضلية من المرتبة الثانية والدرجة الأولى.
عندما يكون للمعادلة السابقة الشكل
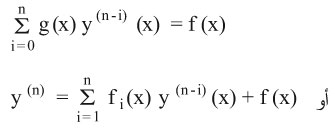
حيث: y(0) (x) = y (x)
فإنها تدعى معادلة خطية من المرتبة n، والمعادلة
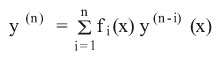
تدعى معادلة خطية متجانسة من المرتبة n، أو يقال إنها معادلة تفاضلية خطية من المرتبة n من دون طرف ثانٍ.
أما المعادلة التفاضلية
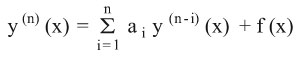
فتدعى معادلة تفاضلية خطية من المرتبة n ذات أمثال ثابتة.
والمعادلة
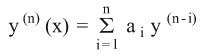
تدعى معادلة تفاضلية خطية متجانسة من المرتبة n ذات أمثال ثابتة. والمعاملات الثوابت a1, a2, …, an هي أعداد حقيقية.
مثال (3): المعادلة y// - 7 y/ + 10 y = sin x معادلة تفاضلية من المرتبة الثانية ذات أمثال ثابتة.
حل معادلة تفاضلية
تكون الدالة y = g (x) حلاً للمعادلة التفاضلية العادية إذا كانت المشتقات المتتالية y/ = g / (x), y// = g// (x), …, y (n) = g(n) (x) موجودة، وتبديلها في المعادلة التفاضلية يحوِّل المعادلة إلى مطابقة. وفي بعض الأحيان قد يعطى الحل بشكل دالة ضمنية F (x, y) = 0 أو بالشكل الوسيطي x = x (t), y = y (t)
وعملية إيجاد الحل لمعادلة تفاضلية تسمى مكاملة هذه المعادلة وهي مسألة معاكسة للحساب التفاضلي، والحل العام general solution للمعادلة التفاضلية من المرتبة n يجب أن يحوي n ثابتاً اختيارياً.
وقد يكون هذا الحل من الشكل الديكارتي y = g (x, c1 , c2 , …, cn) أو من الشكل الوسيطي x = x (t, c1 , c2 , …, cn), y = y (t, c1 , c2 , …, cn) أو من الشكل الضمني F (x, y, c1 , c2 , …, cn) = 0.
ومسألة إيجاد حل للمعادلة التفاضلية يحقق هو ومشتقاته شروطاً إضافية معطاة هي من المسائل المهمة التي تندرج تحت اسم مسألة الشروط الابتدائية initial conditions أو مسألة كوشي Cauchy، وعادة هذه الشروط تعطى بالشكل
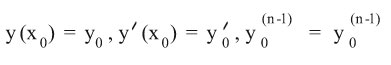
وهندسياً فإن هذا يعني إيجاد منحن تكاملي y = y (x) يمر من النقطة M (x0 , y0) ويحقق الشروط التي ربما ترتبط بخواص هندسية للحصول على أحد منحنيات الأسرة التي تشكل الحل العام. والذي يدعى بالحل الخاص special solution.
ولإيجاد الحل العام للمعادلة التفاضلية الخطية بأمثال حقيقية ثابتة من المرتبة n ذات الشكل:
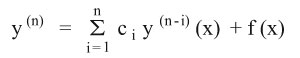
يتم البحث عن جذور المعادلة المميزة لها والتي لها الشكل:
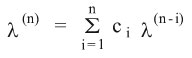
والتي يتم الحصول عليها بتبديل y (n) بالحد λn. وللجذور الحالات الآتية:
أ) الجذور كلها حقيقية ولتكن λ1, λ2, …, λn والحل العام للمعادلة المتجانسة هو
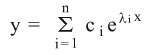
حيث yi = ci e ix (1 ≤ i ≤ n) حلول خاصة وci (1 ≤ i ≤ n) ثوابت كيفية.
مثال (4): المعادلة المميزة للمعادلة التفاضلية المتجانسةy// - y/ - 2y = 0 هي λ2 - λ - 2 = 0 جذراها λ1 = -1 وλ2 = 2 وحلها العام y = c1e-x + c2e2x
ب) بعض الجذور حقيقية والحل الموافق لها كما سبق في المثال (4). وأخرى عقدية مترافقة λm = αm ± i βm والحل الموافق لجذرين مترافقين هو amx (cmcos βmx + c/m sin βmx)
حيثc/m cm ثابتان كيفيان حقيقيان. والحل الخاص للمعادلة هو كل حل يحققها.
هذا وإن الحل العام للمعادلة الخطية غير المتجانسة هو مجموع حلين الأول حل عام لمتجانستها، والآخر هو حل خاص لغير المتجانسة.
بعض أنواع المعادلات التفاضلية العادية من المرتبة الأولى
أ) إن أبسط أنواع المعادلات التفاضلية العادية هي ذات الشكل:

فالمسألة تؤول لحساب تكامل الطرف الأيمن.
ب) إن المعادلة M (x, y) dx + N (x, y) dy = 0 تسمى ذات متحولات قابلة للفصل إذا أمكن ردها للشكل j (x) dx +g ( y) dy = 0 وحلها يعطى بالعلاقة ∫j (x) dx + ∫ g (y) dy = C، حيث C ثابت كيفي.
ج) المعادلة M (x, y) dx + N (x, y) dy = 0 تسمى متجانسة إذا كان تابعاها M (x, y), N (x, y) متجانسين ومن مرتبة التجانس نفسها أي إذا كان M (tx, ty) = tm M (x, y) وN (tx, ty) = tm N (x, y) أو بشكل آخر إذا أمكن كتابتها بالشكل
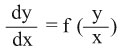
ولحلها يجرى التبديل y = zx ومنه dy = zdx + xdz لترد بعد التبديل إلى معادلة تفاضلية قابلة للفصل.
د)
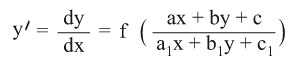
حيث (a, b, c, a1, b1, c1) ثوابت ترد لمعادلة متجانسة.
هـ) المعادلة التفاضلية y/ + p (x) y = q (x) تدعى معادلة خطية من المرتبة الأولى وحلها بالشكل y = e- ∫ p (x) dx [C + ∫ q (x)e ∫ p (x) dx dx] حيث C ثابت كيفي.
و) المعادلة التفاضلية y/ + p (x) y = q (x) y// تدعى معادلة برنولي Bernoulli وهي ترد لمعادلة تفاضلية خطية بالتبديل z = y1 - n وdz = (1 - n) y-n dy وتحل عندها كمعادلة خطية.
ز) المعادلة y/ = p (x) y2 + q (x) y + r (x) وتدعى معادلة ريكاتي Riccati، ومعرفة حل خاص لها y = y1 يسهل حلها بإجراء التبديل
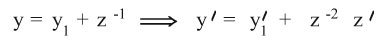
الذي يردها لمعادلة خطية.
ح) المعادلة M (x, y) dx + N (x, y) dy = 0 تكون معادلة تامة إذا حققت العلاقة
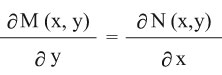
وحلها له الشكل
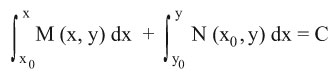
أو
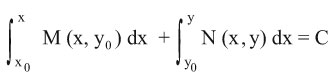
محيي الدين بحبوح
