تويت
معادلات تفاضليه جزييه
Partial differential equations - Equations différentielles partielles
المعادلات التفاضلية الجزئية
المعادلة التفاضلية الجزئية partial differential equation هي المعادلة التي تحوي مشتقاً جزئياً واحداً أو أكثر لتابع (دالة) مجهول يتعلق بمتغيرين مستقلين أو أكثر، فإذا كان التابع المجهول هو z مثلاً وكانت المتغيرات المستقلة هي x1, x2, …, xn فالمعادلة التفاضلية الجزئية تأخذ الشكل الآتي:
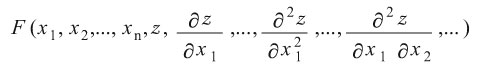
وتعد مرتبةُ المعادلة هي مرتبةَ أعلى مشتق يرد فيها. وكما في المعادلات التفاضلية العادية [ر] يقال إنها خطية إذا كانت من الدرجة الأولى في التابع المجهول ومشتقاته الجزئية. ومن أبرز الأمثلة عملياً على معادلات تفاضلية جزئية وخطية من المرتبة الثانية المعادلات الآتية:
حيث c ثابت يأخذ معنى فيزيائياًيختلف من معادلة لأخرى وt هو الزمن وx, y, z الإحداثيات الديكارتية. إذا كان f(x, y)≠0 في معادلة بواسون ثنائية البعد سميت غير متجانسة، أما إذا كان f(x, y) = 0 فإنها تدعى معادلة متجانسة.
إن حل معادلة تفاضلية جزئية في ساحة ما G من فضاء المتغيرات المستقلة هو تابع z له تلك المشتقات الجزئية التي تظهر في المعادلة، وذلك في الساحة G نفسها ويحقق المعادلة التفاضلية الجزئية في كل نقطة من G.
ولسوء الحظ لا توجد طريقة عامة لإيجاد حلول للمعادلات التفاضلية الجزئية، فالتوابع الآتية على سبيل المثال:
u = x2 - y2 , u = ex cos y , u = In (x2 + y2 ) x
تمثل كلها حلولاً لمعادلة لابلاس ثنائية البعد على الرغم من الاختلاف الكبير فيما بينها. ولإيجاد حل وحيد خاص لمعادلة تفاضلية جزئية تستخدم شروط البدء (أي قيم الحلول عندما تكون t = 0) كما تستخدم ما يسمى شروط الحدود (الشروط الحدَّية) Boundary conditions وهي قيم الحلول في نقاط معينة على حدود الساحة G.
وفيما يلي بعض الأمثلة التي تبين طرائق مكاملة بعض المعادلات التفاضلية الجزئية البسيطة:
مثال (1):
حيث ϕ (y) تابع كيفي لـ y، وهو يقوم بدور الثابت الكيفي عند مكاملة معادلة تفاضلية عادية.
مثال (2):
نكامل مرة ثانية بالنسبة لـ x فنحصل على
z = ò j (y) dy + y (x)
حيث y (x) هو تابع كيفي لـ x.
وهكذا يلاحظ أن الحل العام للمعادلة التفاضلية الجزئية من المرتبة الأولى يتعلق بتابع كيفي واحد، أما الحل العام للمعادلة التفاضلية الجزئية من المرتبة الثانية فيتعلق بتابعين كيفيين... وهكذا.
المعادلة التفاضلية الجزئية الخطية من المرتبة الأولى
تأخذ المعادلة التفاضلية الجزئية الخطية من المرتبة الأولى الشكل الآتي:
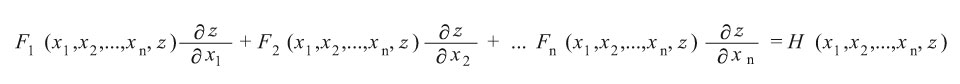
يتضح هنا أن التابع المجهول هو z، فإذا كان H (x1, x2, …, xn, z) = 0
وكانت التوابع F1. F2, …, Fn غير تابعة لـ z يقال عن المعادلة إنها خطية متجانسة.
لتكن لدينا المعادلة:
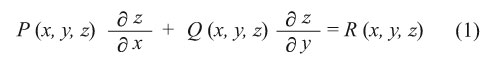
حيث P, Q, R هي توابع مستمرة بالنسبة للمتغيرات ولا تنعدم جميعها في وقت واحد. لا بد لحل هذه المعادلة من الاستعانة بالمفاهيم الهندسية حيث يعتبر حقل المتجهات المستمر F المعرف بالعلاقة:
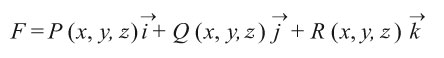
حيث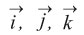
متجهات الواحدة، وهكذا فإن هذه العلاقة تعرِّف متجهاً في كل نقطة من الفضاء.
والمطلوب إيجاد المنحنيات التي تمس في كل نقطة منها المتجه المعرف في تلك النقطة بالعلاقة السابقة.
تتعين هذه المنحنيات من شرط الارتباط الخطي بين المتجه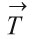
حيث:
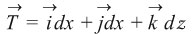
المحمول على المماس في نقطة ما من المنحني المطلوب إيجاده وبين المتجه من الحقل F[ر. الفضاء المتجهي] الموافق لتلك النقطة، ويأخذ الشرط الشكل الآتي:
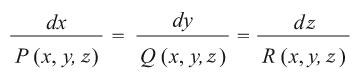
وتشكل جملة المنحنيات المحققة لهذا الشرط سطوحاً تحوي هذه المنحنيات.
وطريقة تشكيل هذه السطوح توضح أن العمود N في كل نقطة من السطح يتعامد مع متجه الحقل F في تلك النقطة أي N. F = 0[ر. الفضاء المتجهي]. وهذا يعني أن معادلات هذه السطوح هي في الواقع حلول المعادلة (1).
فإذا كانت معادلة السطح هي z = f (x, y) فإن المتجه N يأخذ الشكل:
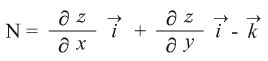
وبالتالي فإن الشرط N. F = 0 يكتب بالشكل:
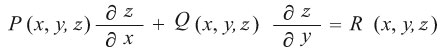
وهذه ليست إلا المعادلة التفاضلية الجزئية الأصلية (1).
أما إذا كانت معادلة السطح u (x, y, z) = 0 فإن N يعطى بالعلاقة:
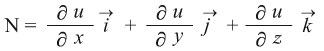
كما أن الشرط N. F = 0 يصبح:
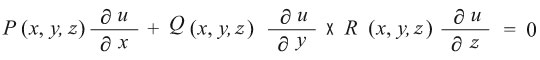
وهكذا فلإيجاد السطوح المحققة للخاصة أي لإيجاد حلول المعادلة التفاضلية الجزئية المعطاة تتبع الخطوات الآتية:
(1) تُؤخذ جملة المعادلات التفاضلية المساعدة
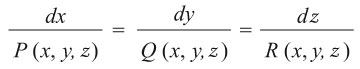
(2) إيجاد تكاملين أوليين مستقلين لهذه الجملة
y1 (x, y, z) = c1, y2 (x, y, z) = c2
فيكون الحل العام للمعادلة التفاضلية الجزئية
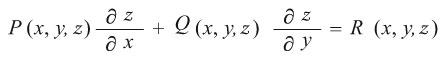
هو السطح التكاملي Φ [y1(x, y, z) , y2(x, y, z)] حيث Φ هو تابع اختياري. أما إيجاد قيمتي الثابتين c1, c2 فيعني إيجاد ذلك السطح التكاملي المار من منحنٍ ما بالذات Γ مثلاً.
فإذا فرض أن معادلات المنحني معطاة بدلالة تقاطع السطحين يكون:
f (x, y, z) = 0, g (x, y, z) = 0
فإنه يتم إيجاد معادلة السطح التكاملي بإيجاد علاقة بين c1, c2 من المعادلات:
f (x, y, z) = 0, g (x, y, z) = 0
y1(x, y, z) = c1, y2(x, y, z) = c2
فإذا كانت هذه العلاقة هي S (c1, c2) = 0 فإن معادلة السطح التكاملي المار من المنحني Γ تأخذ الشكل
S [y1(x, y, z), y2(x, y, z)] = 0
المعادلة التفاضلية الجزئية الخطية من المرتبة الثانية
تعد المعادلة التفاضلية الجزئية الخطية من المرتبة الثانية من أهم المعادلات التفاضلية الجزئية في المسائل التطبيقية (الفيزيائية مثلاً). يتم تصنيف المعادلات التفاضلية الجزئية الخطية من المرتبة الثانية في أربعة أنواع رئيسية:
أ - المعادلة التفاضلية الجزئية من النوع الناقصي، وتكتب بالشكل:
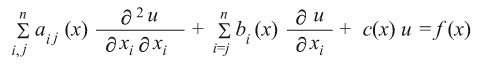
بفرض x = (x1, x2, …, xn) ; aij = aji، وأن G هي المنطقة التي تقع فيها المتغيرات المستقلة، وبحيث يتحقق الشرط:
م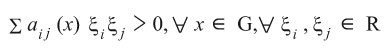
فمن أجل n = 2 مثلاً، فإن:
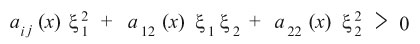
إذا كان:
(2a12)2 - 4 a11a12 < 0 ; a11 > 0
ب - المعادلة التفاضلية الجزئية من النوع الزائد:
تسمى المعادلة الخطية في المتغيرات t , x1, x2, …, xnوالمعطاة بالشكل:
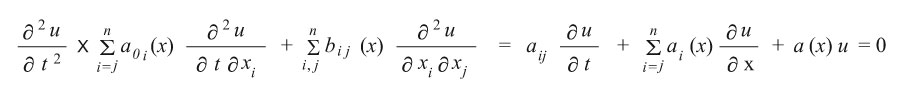
حيث a0i , …, aij هي توابع (دوال) في t وx، بمعادلة من النوع المكافئ بالاتجاه t في الفضاء tx إذا كان للمعادلة المميزة
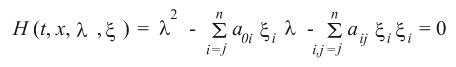
جذران حقيقيان l1 ( t, x, x ) , l2 (t, x , x) من أجل أي مرتّب من n
x = (x1, …, xn ) ≠ ( 0, …, 0).
ج ـ المعادلة التفاضلية الجزئية من النوع المكافىء:
تسمى المعادلة
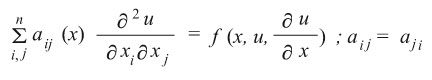
معادلة من النوع المكافئ إذا وفقط إذا كان det (aij) = 0 في كل نقطة من نقط الساحة المطروحة للدراسة.
د ـ المعادلة التفاضلية الجزئية من النوع المختلط
وهي معادلة تفاضلية جزئية لا تنتمي إلى أي من الأنواع السابقة ومن أشهر هذه المعادلات هي:
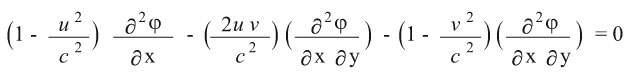
حيث:
فوزي دنان
Partial differential equations - Equations différentielles partielles
المعادلات التفاضلية الجزئية
المعادلة التفاضلية الجزئية partial differential equation هي المعادلة التي تحوي مشتقاً جزئياً واحداً أو أكثر لتابع (دالة) مجهول يتعلق بمتغيرين مستقلين أو أكثر، فإذا كان التابع المجهول هو z مثلاً وكانت المتغيرات المستقلة هي x1, x2, …, xn فالمعادلة التفاضلية الجزئية تأخذ الشكل الآتي:
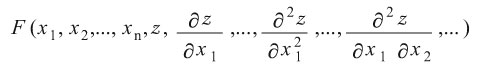
وتعد مرتبةُ المعادلة هي مرتبةَ أعلى مشتق يرد فيها. وكما في المعادلات التفاضلية العادية [ر] يقال إنها خطية إذا كانت من الدرجة الأولى في التابع المجهول ومشتقاته الجزئية. ومن أبرز الأمثلة عملياً على معادلات تفاضلية جزئية وخطية من المرتبة الثانية المعادلات الآتية:
حيث c ثابت يأخذ معنى فيزيائياًيختلف من معادلة لأخرى وt هو الزمن وx, y, z الإحداثيات الديكارتية. إذا كان f(x, y)≠0 في معادلة بواسون ثنائية البعد سميت غير متجانسة، أما إذا كان f(x, y) = 0 فإنها تدعى معادلة متجانسة.
إن حل معادلة تفاضلية جزئية في ساحة ما G من فضاء المتغيرات المستقلة هو تابع z له تلك المشتقات الجزئية التي تظهر في المعادلة، وذلك في الساحة G نفسها ويحقق المعادلة التفاضلية الجزئية في كل نقطة من G.
ولسوء الحظ لا توجد طريقة عامة لإيجاد حلول للمعادلات التفاضلية الجزئية، فالتوابع الآتية على سبيل المثال:
u = x2 - y2 , u = ex cos y , u = In (x2 + y2 ) x
تمثل كلها حلولاً لمعادلة لابلاس ثنائية البعد على الرغم من الاختلاف الكبير فيما بينها. ولإيجاد حل وحيد خاص لمعادلة تفاضلية جزئية تستخدم شروط البدء (أي قيم الحلول عندما تكون t = 0) كما تستخدم ما يسمى شروط الحدود (الشروط الحدَّية) Boundary conditions وهي قيم الحلول في نقاط معينة على حدود الساحة G.
وفيما يلي بعض الأمثلة التي تبين طرائق مكاملة بعض المعادلات التفاضلية الجزئية البسيطة:
مثال (1):
حيث ϕ (y) تابع كيفي لـ y، وهو يقوم بدور الثابت الكيفي عند مكاملة معادلة تفاضلية عادية.
مثال (2):
نكامل مرة ثانية بالنسبة لـ x فنحصل على
z = ò j (y) dy + y (x)
حيث y (x) هو تابع كيفي لـ x.
وهكذا يلاحظ أن الحل العام للمعادلة التفاضلية الجزئية من المرتبة الأولى يتعلق بتابع كيفي واحد، أما الحل العام للمعادلة التفاضلية الجزئية من المرتبة الثانية فيتعلق بتابعين كيفيين... وهكذا.
المعادلة التفاضلية الجزئية الخطية من المرتبة الأولى
تأخذ المعادلة التفاضلية الجزئية الخطية من المرتبة الأولى الشكل الآتي:
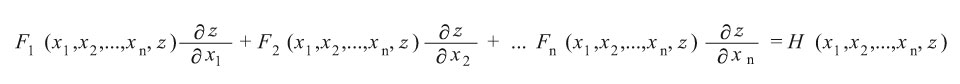
يتضح هنا أن التابع المجهول هو z، فإذا كان H (x1, x2, …, xn, z) = 0
وكانت التوابع F1. F2, …, Fn غير تابعة لـ z يقال عن المعادلة إنها خطية متجانسة.
لتكن لدينا المعادلة:
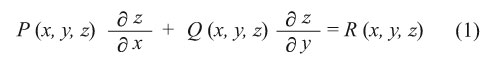
حيث P, Q, R هي توابع مستمرة بالنسبة للمتغيرات ولا تنعدم جميعها في وقت واحد. لا بد لحل هذه المعادلة من الاستعانة بالمفاهيم الهندسية حيث يعتبر حقل المتجهات المستمر F المعرف بالعلاقة:
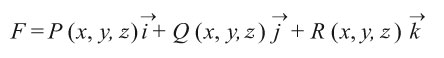
حيث
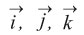متجهات الواحدة، وهكذا فإن هذه العلاقة تعرِّف متجهاً في كل نقطة من الفضاء.والمطلوب إيجاد المنحنيات التي تمس في كل نقطة منها المتجه المعرف في تلك النقطة بالعلاقة السابقة.
تتعين هذه المنحنيات من شرط الارتباط الخطي بين المتجه
حيث: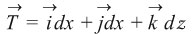المحمول على المماس في نقطة ما من المنحني المطلوب إيجاده وبين المتجه من الحقل F[ر. الفضاء المتجهي] الموافق لتلك النقطة، ويأخذ الشرط الشكل الآتي:
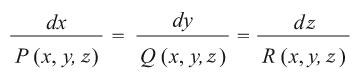
وتشكل جملة المنحنيات المحققة لهذا الشرط سطوحاً تحوي هذه المنحنيات.
وطريقة تشكيل هذه السطوح توضح أن العمود N في كل نقطة من السطح يتعامد مع متجه الحقل F في تلك النقطة أي N. F = 0[ر. الفضاء المتجهي]. وهذا يعني أن معادلات هذه السطوح هي في الواقع حلول المعادلة (1).
فإذا كانت معادلة السطح هي z = f (x, y) فإن المتجه N يأخذ الشكل:
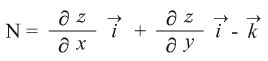
وبالتالي فإن الشرط N. F = 0 يكتب بالشكل:
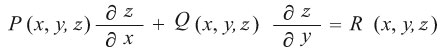
وهذه ليست إلا المعادلة التفاضلية الجزئية الأصلية (1).
أما إذا كانت معادلة السطح u (x, y, z) = 0 فإن N يعطى بالعلاقة:
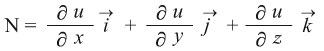
كما أن الشرط N. F = 0 يصبح:
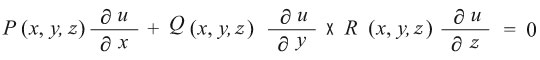
وهكذا فلإيجاد السطوح المحققة للخاصة أي لإيجاد حلول المعادلة التفاضلية الجزئية المعطاة تتبع الخطوات الآتية:
(1) تُؤخذ جملة المعادلات التفاضلية المساعدة
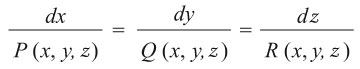
(2) إيجاد تكاملين أوليين مستقلين لهذه الجملة
y1 (x, y, z) = c1, y2 (x, y, z) = c2
فيكون الحل العام للمعادلة التفاضلية الجزئية
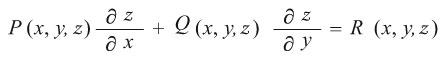
هو السطح التكاملي Φ [y1(x, y, z) , y2(x, y, z)] حيث Φ هو تابع اختياري. أما إيجاد قيمتي الثابتين c1, c2 فيعني إيجاد ذلك السطح التكاملي المار من منحنٍ ما بالذات Γ مثلاً.
فإذا فرض أن معادلات المنحني معطاة بدلالة تقاطع السطحين يكون:
f (x, y, z) = 0, g (x, y, z) = 0
فإنه يتم إيجاد معادلة السطح التكاملي بإيجاد علاقة بين c1, c2 من المعادلات:
f (x, y, z) = 0, g (x, y, z) = 0
y1(x, y, z) = c1, y2(x, y, z) = c2
فإذا كانت هذه العلاقة هي S (c1, c2) = 0 فإن معادلة السطح التكاملي المار من المنحني Γ تأخذ الشكل
S [y1(x, y, z), y2(x, y, z)] = 0
المعادلة التفاضلية الجزئية الخطية من المرتبة الثانية
تعد المعادلة التفاضلية الجزئية الخطية من المرتبة الثانية من أهم المعادلات التفاضلية الجزئية في المسائل التطبيقية (الفيزيائية مثلاً). يتم تصنيف المعادلات التفاضلية الجزئية الخطية من المرتبة الثانية في أربعة أنواع رئيسية:
أ - المعادلة التفاضلية الجزئية من النوع الناقصي، وتكتب بالشكل:
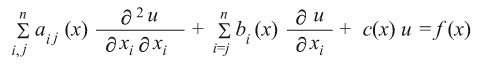
بفرض x = (x1, x2, …, xn) ; aij = aji، وأن G هي المنطقة التي تقع فيها المتغيرات المستقلة، وبحيث يتحقق الشرط:
م
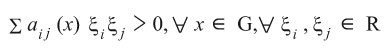
فمن أجل n = 2 مثلاً، فإن:
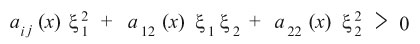
إذا كان:
(2a12)2 - 4 a11a12 < 0 ; a11 > 0
ب - المعادلة التفاضلية الجزئية من النوع الزائد:
تسمى المعادلة الخطية في المتغيرات t , x1, x2, …, xnوالمعطاة بالشكل:
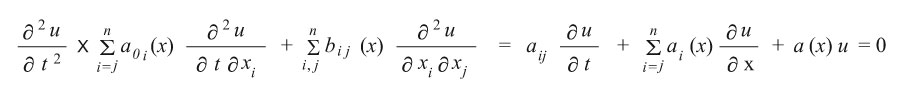
حيث a0i , …, aij هي توابع (دوال) في t وx، بمعادلة من النوع المكافئ بالاتجاه t في الفضاء tx إذا كان للمعادلة المميزة
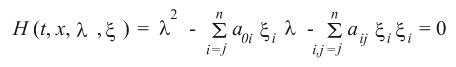
جذران حقيقيان l1 ( t, x, x ) , l2 (t, x , x) من أجل أي مرتّب من n
x = (x1, …, xn ) ≠ ( 0, …, 0).
ج ـ المعادلة التفاضلية الجزئية من النوع المكافىء:
تسمى المعادلة
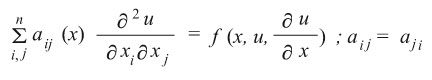
معادلة من النوع المكافئ إذا وفقط إذا كان det (aij) = 0 في كل نقطة من نقط الساحة المطروحة للدراسة.
د ـ المعادلة التفاضلية الجزئية من النوع المختلط
وهي معادلة تفاضلية جزئية لا تنتمي إلى أي من الأنواع السابقة ومن أشهر هذه المعادلات هي:
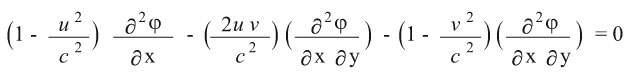
حيث:
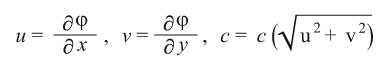
فوزي دنان