تويت
مبدا تتاميه
Complementarity principle - Principe de complémentarité
مبدأ التتامية
مبدأ التتامية (أو التكاملية) complementarity principle، مبدأٌ في فيزياء الكمّ ينصّ على أن المعرفةَ الكاملة لظاهرةٍ فيزيائية على المستوى الذري تتطلّب وصفاً للخواص الجسيمية والموجية معاً لهذه الظاهرة. أعلن هذا المبدأ عام 1927 العالِم الدنماركي نيلز بور[ر] Niels Bohr كما يأتي: «من المستحيل قياس جميع الخصائص المميِّزة لمنظومة ذرية بالدقة التي نريد عن طريق إجراء تجربة واحدة، إذ توجد مقادير فيزيائية متتامة يُكمل بعضها بعضاً، ولا يمكن تعريفها بدقة إلاّ باستخدام أجهزة قياس مختلفة. تعني صفة التتامية هنا أن اجتماعَ هذه المقادير المتتامة هو ما يمثّل مجملَ المعلومات التي تصف الظاهرةَ الذرية، على الرغم من أنه لا يمكن دمجها جميعاً في توصيف وحيد».
يعود هذا إلى اعتماد سلوك المنظومة المجهرية (مثل الضوء أو الإلكترونات) على جهاز القياس المستخدَم، فوفقاً له تسلك المنظومة سلوكَ جسيماتٍ أو سلوكَ أمواجٍ، ولا يمكن ملاحظة السلوكين معاً، ومع ذلك يقدّم كلاهما معاً الصورةَ الكاملة لوصف المنظومة.
وحسب هذا المبدأ، ليست خصائص الظاهرة الفيزيائية على المستوى الذري وما دونه خصائصَ جسيماتٍ أو أمواجٍ ممّا اعتدنا عليه في المستوى العياني macroscopic (مثل كرات البلياردو أو أمواج الماء)، فبينما لا يمكن للخصائص الجسيمية والموجية أن توجد معاً على المستوى العياني، فإنه لا بدّ من أخذ المظهرين معاً عند وصف ظاهرةٍ على المستوى الذري.
مبدأ التتامية ومبدأ الارتياب في ميكانيك الكم
يرتبط مبدأ التتامية ارتباطاً وثيقاً بمبدأ الارتياب uncertainty principle الذي أعلنه في السنة نفسها (1927) العالِم الألماني فرنر هايزنبرغ[ر] Werner Karle Heisenberg. يمكن استنتاج المبدأ الأخير ابتداءً من مسلّمات نظرية الكمّ ويعبَّر عنه بعلاقاتٍ رياضياتية محدّدة، في حين يعكس مبدأ التتامية الأثرَ العميق الناجم عن مبدأ الارتياب على طريقتنا في التفكير لفهم الظواهر المجهرية.
ينصّ مبدأ الارتياب في صيغته الأولى على أنه لايمكن، ولو نظرياً، تحديد موضع وسرعة جسيم ما في الوقت نفسه وبدقّة لا متناهية. إن مفهوم التحديد التامّ للموضع والسرعة معاً لا وجود له في الطبيعة.
لا تقدّم التجارب العادية دليلاً على صحة هذا المبدأ، إذ من السهولة تحديد موضع وسرعة جسمٍ عياني ما مثل السيارة، وذلك لأن المتراجحات التي يقتضيها مبدأ الارتياب تتضمّن قيماً صغيرة يصعب ملاحظتها من أجل أجسام كبيرة. تقول هذه المتراجحات إن حاصل جداء قيمة الارتياب في الموضع في قيمة الارتياب في الاندفاع أكبر أو يساوي قيمة ثابت بلانك مقسومة على 2π أي: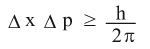
. إن أي محاولة لقياس سرعة جسيم ذري مثل الإلكترون سوف تزيحه عن موضعه بشكل لا يمكن التنبؤ به، ممّا يجعل القياس الدقيق للسرعة والموضع معاً مستحيلاً. إن هذا الأمر ليس نتيجةً لعدم كمال الأجهزة التجريبية أو تقنيات المراقب بل هو نتيجة للعلاقة الوثيقة في الطبيعة بين المظهرين الجسيمي والموجي على المستوى المجهري، والتي يعبَّر عنها بثنوية الجسيم - الموجة wave-particle duality. تاريخياً، يرجع مفهوم الثنوية إلى اقتراح أينشتاين[ر] Einstein عام 1905، والمبني على أسس تجريبية، في أننا يجب أن ننظر إلى الضوء كمجموعةِ جسيماتٍ، إضافة إلى وصفه كأمواج كهرطيسية. اقترح بعد ذلك الفيزيائي الفرنسي لوي دو بروي[ر] Louis de Broglie عام 1924 أن الجسيمات، مثل الإلكترونات، تملك كذلك خصائص موجية مثل الطول الموجي والتواتر، وقد بُرهن تجريبياً على الطبيعة الموجية للإلكترونات عام 1927 في تجارب انعراج الإلكترونات.
تمّت صياغة هذه الأفكار رياضياتياً، في ميكانيك الكمّ الذي يربط بكلّ جسيم تابعاً موجياً، يصف حركته حيث يكون احتمالُ وجودِ الجسيم أكبرَ ما يمكن في الأماكن التي تكون فيها قيم هذا التابع الموجي أعظمية. كلما ازدادت التفاوتات في التابع الموجي للجسيم ازداد الارتياب في قيمة طول موجة الجسيم، الذي يحدّد اندفاعَه p أو سرعته (وفق علاقة دو بروي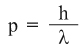
حيث λ طول الموجة). يعني ذلك أنه لا يمكن تحديد الطول الموجي من أجل تابع موجي متمركز في نقطة واحدة، لأن التفاوت في قيم التابع الموجي عند هذه النقطة ومجاوراتها تكون أعظمية، ومن ثمّ لا يمكن تحديد سرعة الجسيم إذا عرفنا موضعه بدقة. وبالعكس، تمتدّ الموجة ذات الطول الموجي المحدَّد بدقة (أي الاندفاع والسرعة المحددين بدقة) في أرجاء الفضاء، فلا يمكن القول أين يكمن تموضعُها. يعني ذلك أنه لا يمكن تحديد موضعِ جسيمٍ إذا ما عرفنا قيمة سرعته بدقة.
لايقتصر مبدأ الارتياب فقط على استحالة تحديد السرعة والموضع معاً، بل إن هناك مقاديرَ فيزيائية أخرى لا يمكن تحديدها بدقة في الوقت نفسه. مثال على ذلك علاقة الارتياب للطاقة والزمن، وتُكتب رياضياتياً على الشكل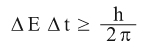
يرمز ΔE هنا إلى الارتياب في قيمة طاقة جسيمٍ ما، في حين يرمز Δt إلى الارتياب في قيمة طول المدة الزمنية التي تمّ قياس الطاقة خلالها، وغالباً ما يمثّل الارتياب في لحظة مرور الجسيم في نقطةٍ ما (يوجد فيها جهاز قياس الطاقة). من أجل منظومات غير مستقرّة، يعبّر ΔE عن الارتياب في قيمة الطاقة المشَعّة عندما تنتقل المنظومة من مستوى طاقي إلى آخرٍ أدنى، بينما يعبّر Δt عن الارتياب في زمن وجودها في المستوى الأقل استقراراً قبل انتقالها إلى المستوى الأكثر استقراراً.
الشواهد التجريبية والنتائج الفلسفية لمبدأ التتامية
قلبت علاقات الارتياب التي يقتضيها ميكانيك الكمّ جذرياً طريقةَ التفكير التي اكتُسبت من الميكانيك الكلاسيكي. وقد حاول كثير من الفيزيائيين ابتداع تجارب ذهنية يمكن بوساطتها قياس الاندفاع والموضع لجسيم ما، ولكن التحليلَ الدقيق للمنظومة الفيزيائية المدروسة مع الجهاز التجريبي بيّن أن علاقات الارتياب محقّقة دوماً، حيث لا يمكن التحديد التام لأحد المقدارين الفيزيائيين اللذين تتضمنهما علاقة الارتياب، إلاّ إذا تخلّينا عن إمكان قياس المقدار الآخر. بدا إذن أن الفيزياء الكمومية عاجزة عن الوصف الكامل للظواهر الذرية.
قاد هذا الاستنتاج الخاطئ العالم بور إلى مفهوم التتامية، الذي يؤكّد استحالة الفصل بين سلوك المنظومات الذرية وبين تآثرها مع أجهزة القياس التي تسمح برصدها. إن الاجتماع غير القابل للفصل بين المنظومة الذرية مع جهاز القياس هو ما يعرّف الظاهرةَ الفيزيائية؛ ففي حال غيّرنا جهاز القياس فإننا نكون قد غيّرنا هذا الاجتماع، ومن ثم تكون الظاهرة الفيزيائية المدروسة قد تغيّرت. تسمح النظرية الكمومية إذن بالتنبّؤ الكامل بنتائج تجربةٍ ما شريطةَ تحديدنا لجهاز القياس، وضمن هذا المعنى تزوّدنا هذه النظرية بالوصف الكامل للظواهر الفيزيائية. مع ذلك، من أجل تقديم هذا الوصف الكامل، من الضروري عدُّ جهاز القياس جزءاً لا يتجزّأ من الظاهرة المدروسة، فالنظرية لا تسمح بالحديث عن خواصّ منظومة فيزيائية على نحو مطلق، بل تقدّم لنا وصفاً لكيفية تفاعلها مع جهاز القياس هذا أو ذاك.
توجد أجهزة قياس تسمح بالتحديد التام لموضع الجسيم، ولكنها في هذه الحالة غير قادرة على تعيين سرعته، ولابدّ من استعمال أجهزة قياس أخرى، أي دراسة ظواهر فيزيائية أخرى، من أجل تحديد السرعة. لا يستطيع أيٌّ من الوصفين الموافقين لتجربة تحديد الموضع وتجربة تحديد السرعة تقديمَ مجمل المعلومات التي تصف الجسيم، ولكن كلاً منهما يؤلف وصفاً مكمّلاً (أو متمّماً) للوصف الآخر. لذلك يوصف متغيّرا الموضع والسرعة بأنهما متغيّران متتامان complementary variables.
يسمح مفهوم التتامية هذا بفهمٍ أعمق لثنوية الجسيم - الموجة. توافق الخواصُّ الجسيمية للمنظومة المدروسة إمكان تحديد موضع المنظومة في مكان محدّد عند لحظة معطاة، في حين توافق الخواص الموجية للمنظومة نفسها إمكان شغلِ هذه المنظومة لمنطقةٍ ممتدة في الفضاء. يبدو هذان المظهران للخواص متناقضين للوهلة الأولى، ولكنهما في الحقيقة متتامين. يتجسّد أحد هذين المظهرين دون الآخر، وفقاً للجهاز التجريبي المستخدم، فمثلاً تُبرز التجارب الكلاسيكية في الضوء الموجي (التداخل والانعراج) الخواصَ الموجية للإشعاع الكهرطيسي، في حين تُبرز تجارب أخرى مثل المفعول الكهرضوئي ومفعول كومبتون الخواصَ الجسيمية للإشعاع نفسه، وتقود إلى الحديث عن كمّات الضوء - الفوتونات [ر]. إن هذين النوعين من التجارب متكاملان، ولابدّ من كليهما من أجل تقديم التوصيف الكامل للضوء، أو لأي منظومة ذرية عموماً.
نضال شمعون
Complementarity principle - Principe de complémentarité
مبدأ التتامية
مبدأ التتامية (أو التكاملية) complementarity principle، مبدأٌ في فيزياء الكمّ ينصّ على أن المعرفةَ الكاملة لظاهرةٍ فيزيائية على المستوى الذري تتطلّب وصفاً للخواص الجسيمية والموجية معاً لهذه الظاهرة. أعلن هذا المبدأ عام 1927 العالِم الدنماركي نيلز بور[ر] Niels Bohr كما يأتي: «من المستحيل قياس جميع الخصائص المميِّزة لمنظومة ذرية بالدقة التي نريد عن طريق إجراء تجربة واحدة، إذ توجد مقادير فيزيائية متتامة يُكمل بعضها بعضاً، ولا يمكن تعريفها بدقة إلاّ باستخدام أجهزة قياس مختلفة. تعني صفة التتامية هنا أن اجتماعَ هذه المقادير المتتامة هو ما يمثّل مجملَ المعلومات التي تصف الظاهرةَ الذرية، على الرغم من أنه لا يمكن دمجها جميعاً في توصيف وحيد».
يعود هذا إلى اعتماد سلوك المنظومة المجهرية (مثل الضوء أو الإلكترونات) على جهاز القياس المستخدَم، فوفقاً له تسلك المنظومة سلوكَ جسيماتٍ أو سلوكَ أمواجٍ، ولا يمكن ملاحظة السلوكين معاً، ومع ذلك يقدّم كلاهما معاً الصورةَ الكاملة لوصف المنظومة.
وحسب هذا المبدأ، ليست خصائص الظاهرة الفيزيائية على المستوى الذري وما دونه خصائصَ جسيماتٍ أو أمواجٍ ممّا اعتدنا عليه في المستوى العياني macroscopic (مثل كرات البلياردو أو أمواج الماء)، فبينما لا يمكن للخصائص الجسيمية والموجية أن توجد معاً على المستوى العياني، فإنه لا بدّ من أخذ المظهرين معاً عند وصف ظاهرةٍ على المستوى الذري.
مبدأ التتامية ومبدأ الارتياب في ميكانيك الكم
يرتبط مبدأ التتامية ارتباطاً وثيقاً بمبدأ الارتياب uncertainty principle الذي أعلنه في السنة نفسها (1927) العالِم الألماني فرنر هايزنبرغ[ر] Werner Karle Heisenberg. يمكن استنتاج المبدأ الأخير ابتداءً من مسلّمات نظرية الكمّ ويعبَّر عنه بعلاقاتٍ رياضياتية محدّدة، في حين يعكس مبدأ التتامية الأثرَ العميق الناجم عن مبدأ الارتياب على طريقتنا في التفكير لفهم الظواهر المجهرية.
ينصّ مبدأ الارتياب في صيغته الأولى على أنه لايمكن، ولو نظرياً، تحديد موضع وسرعة جسيم ما في الوقت نفسه وبدقّة لا متناهية. إن مفهوم التحديد التامّ للموضع والسرعة معاً لا وجود له في الطبيعة.
لا تقدّم التجارب العادية دليلاً على صحة هذا المبدأ، إذ من السهولة تحديد موضع وسرعة جسمٍ عياني ما مثل السيارة، وذلك لأن المتراجحات التي يقتضيها مبدأ الارتياب تتضمّن قيماً صغيرة يصعب ملاحظتها من أجل أجسام كبيرة. تقول هذه المتراجحات إن حاصل جداء قيمة الارتياب في الموضع في قيمة الارتياب في الاندفاع أكبر أو يساوي قيمة ثابت بلانك مقسومة على 2π أي:
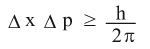. إن أي محاولة لقياس سرعة جسيم ذري مثل الإلكترون سوف تزيحه عن موضعه بشكل لا يمكن التنبؤ به، ممّا يجعل القياس الدقيق للسرعة والموضع معاً مستحيلاً. إن هذا الأمر ليس نتيجةً لعدم كمال الأجهزة التجريبية أو تقنيات المراقب بل هو نتيجة للعلاقة الوثيقة في الطبيعة بين المظهرين الجسيمي والموجي على المستوى المجهري، والتي يعبَّر عنها بثنوية الجسيم - الموجة wave-particle duality. تاريخياً، يرجع مفهوم الثنوية إلى اقتراح أينشتاين[ر] Einstein عام 1905، والمبني على أسس تجريبية، في أننا يجب أن ننظر إلى الضوء كمجموعةِ جسيماتٍ، إضافة إلى وصفه كأمواج كهرطيسية. اقترح بعد ذلك الفيزيائي الفرنسي لوي دو بروي[ر] Louis de Broglie عام 1924 أن الجسيمات، مثل الإلكترونات، تملك كذلك خصائص موجية مثل الطول الموجي والتواتر، وقد بُرهن تجريبياً على الطبيعة الموجية للإلكترونات عام 1927 في تجارب انعراج الإلكترونات.تمّت صياغة هذه الأفكار رياضياتياً، في ميكانيك الكمّ الذي يربط بكلّ جسيم تابعاً موجياً، يصف حركته حيث يكون احتمالُ وجودِ الجسيم أكبرَ ما يمكن في الأماكن التي تكون فيها قيم هذا التابع الموجي أعظمية. كلما ازدادت التفاوتات في التابع الموجي للجسيم ازداد الارتياب في قيمة طول موجة الجسيم، الذي يحدّد اندفاعَه p أو سرعته (وفق علاقة دو بروي
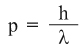حيث λ طول الموجة). يعني ذلك أنه لا يمكن تحديد الطول الموجي من أجل تابع موجي متمركز في نقطة واحدة، لأن التفاوت في قيم التابع الموجي عند هذه النقطة ومجاوراتها تكون أعظمية، ومن ثمّ لا يمكن تحديد سرعة الجسيم إذا عرفنا موضعه بدقة. وبالعكس، تمتدّ الموجة ذات الطول الموجي المحدَّد بدقة (أي الاندفاع والسرعة المحددين بدقة) في أرجاء الفضاء، فلا يمكن القول أين يكمن تموضعُها. يعني ذلك أنه لا يمكن تحديد موضعِ جسيمٍ إذا ما عرفنا قيمة سرعته بدقة.لايقتصر مبدأ الارتياب فقط على استحالة تحديد السرعة والموضع معاً، بل إن هناك مقاديرَ فيزيائية أخرى لا يمكن تحديدها بدقة في الوقت نفسه. مثال على ذلك علاقة الارتياب للطاقة والزمن، وتُكتب رياضياتياً على الشكل
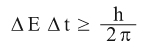يرمز ΔE هنا إلى الارتياب في قيمة طاقة جسيمٍ ما، في حين يرمز Δt إلى الارتياب في قيمة طول المدة الزمنية التي تمّ قياس الطاقة خلالها، وغالباً ما يمثّل الارتياب في لحظة مرور الجسيم في نقطةٍ ما (يوجد فيها جهاز قياس الطاقة). من أجل منظومات غير مستقرّة، يعبّر ΔE عن الارتياب في قيمة الطاقة المشَعّة عندما تنتقل المنظومة من مستوى طاقي إلى آخرٍ أدنى، بينما يعبّر Δt عن الارتياب في زمن وجودها في المستوى الأقل استقراراً قبل انتقالها إلى المستوى الأكثر استقراراً.الشواهد التجريبية والنتائج الفلسفية لمبدأ التتامية
قلبت علاقات الارتياب التي يقتضيها ميكانيك الكمّ جذرياً طريقةَ التفكير التي اكتُسبت من الميكانيك الكلاسيكي. وقد حاول كثير من الفيزيائيين ابتداع تجارب ذهنية يمكن بوساطتها قياس الاندفاع والموضع لجسيم ما، ولكن التحليلَ الدقيق للمنظومة الفيزيائية المدروسة مع الجهاز التجريبي بيّن أن علاقات الارتياب محقّقة دوماً، حيث لا يمكن التحديد التام لأحد المقدارين الفيزيائيين اللذين تتضمنهما علاقة الارتياب، إلاّ إذا تخلّينا عن إمكان قياس المقدار الآخر. بدا إذن أن الفيزياء الكمومية عاجزة عن الوصف الكامل للظواهر الذرية.
قاد هذا الاستنتاج الخاطئ العالم بور إلى مفهوم التتامية، الذي يؤكّد استحالة الفصل بين سلوك المنظومات الذرية وبين تآثرها مع أجهزة القياس التي تسمح برصدها. إن الاجتماع غير القابل للفصل بين المنظومة الذرية مع جهاز القياس هو ما يعرّف الظاهرةَ الفيزيائية؛ ففي حال غيّرنا جهاز القياس فإننا نكون قد غيّرنا هذا الاجتماع، ومن ثم تكون الظاهرة الفيزيائية المدروسة قد تغيّرت. تسمح النظرية الكمومية إذن بالتنبّؤ الكامل بنتائج تجربةٍ ما شريطةَ تحديدنا لجهاز القياس، وضمن هذا المعنى تزوّدنا هذه النظرية بالوصف الكامل للظواهر الفيزيائية. مع ذلك، من أجل تقديم هذا الوصف الكامل، من الضروري عدُّ جهاز القياس جزءاً لا يتجزّأ من الظاهرة المدروسة، فالنظرية لا تسمح بالحديث عن خواصّ منظومة فيزيائية على نحو مطلق، بل تقدّم لنا وصفاً لكيفية تفاعلها مع جهاز القياس هذا أو ذاك.
توجد أجهزة قياس تسمح بالتحديد التام لموضع الجسيم، ولكنها في هذه الحالة غير قادرة على تعيين سرعته، ولابدّ من استعمال أجهزة قياس أخرى، أي دراسة ظواهر فيزيائية أخرى، من أجل تحديد السرعة. لا يستطيع أيٌّ من الوصفين الموافقين لتجربة تحديد الموضع وتجربة تحديد السرعة تقديمَ مجمل المعلومات التي تصف الجسيم، ولكن كلاً منهما يؤلف وصفاً مكمّلاً (أو متمّماً) للوصف الآخر. لذلك يوصف متغيّرا الموضع والسرعة بأنهما متغيّران متتامان complementary variables.
يسمح مفهوم التتامية هذا بفهمٍ أعمق لثنوية الجسيم - الموجة. توافق الخواصُّ الجسيمية للمنظومة المدروسة إمكان تحديد موضع المنظومة في مكان محدّد عند لحظة معطاة، في حين توافق الخواص الموجية للمنظومة نفسها إمكان شغلِ هذه المنظومة لمنطقةٍ ممتدة في الفضاء. يبدو هذان المظهران للخواص متناقضين للوهلة الأولى، ولكنهما في الحقيقة متتامين. يتجسّد أحد هذين المظهرين دون الآخر، وفقاً للجهاز التجريبي المستخدم، فمثلاً تُبرز التجارب الكلاسيكية في الضوء الموجي (التداخل والانعراج) الخواصَ الموجية للإشعاع الكهرطيسي، في حين تُبرز تجارب أخرى مثل المفعول الكهرضوئي ومفعول كومبتون الخواصَ الجسيمية للإشعاع نفسه، وتقود إلى الحديث عن كمّات الضوء - الفوتونات [ر]. إن هذين النوعين من التجارب متكاملان، ولابدّ من كليهما من أجل تقديم التوصيف الكامل للضوء، أو لأي منظومة ذرية عموماً.
نضال شمعون