مجسم قطع ناقص (مرجع)
Reference ellipsoid - Ellipsoïde de référence
مجسم القطع الناقص
مجسم القطع الناقص (المرجع) أو المجسم الناقصي المرجعي reference ellipsoid هو سطح فراغي دوراني، ناتج من دوران قطع ناقص - معرف رياضيًا تعريفاً مناسباً - حول محوره الصغير، بحيث يكون المجسم أقرب ما يمكن إلى الشكل الحقيقي للأرض. ترسم عليه شبكة جيوديزية، تساعد على تعيين إحداثيات نقطة ما باستخدام هذه الشبكة.
سطح الأرض
إن وجه الأرض لا يمثل سطحًا فراغيًا منتظماً، إلا في أجزاء منه، حيث يمكن عدّ المحيطات سطوحًا منتظمة نوعاً ما، في حين التضاريس من جبال وأودية تشير إلى وجود تغيرات شاقولية كبيرة بينها على وجه الأرض فكان من المستحيل على علماء الجيوديزيا Geodesy - (وهو فرع من الرياضيات التطبيقية يهتم بدراسة الأرض، شكلها وأبعادها) - إعطاء نموذج رياضي مبسط ودقيق لسطح الأرض.
كما أن كتلة الأرض غير منتظمة الكثافة؛ مما يجعل قوة الجاذبية (الثقالة) غير ثابتة على سطح الأرض. لذا فإن القول «الأرض مجسم قطع ناقص» غير دقيق، ولكنه أقرب ما يكون للحقيقة.
إن الحاجة ماسة لاتخاذ نموذج رياضي للأرض، حتى يمكن تحديد موضع نقطة ما - على الأرض أو خارجها - بإحداثيات دقيقة، اعتمادًا على خطوط طول وخطوط عرض وارتفاعات محددة بدقة. ولأن سطح مجسم القطع الناقص هو تمثيل أقرب ما يكون لحقيقة وجه الأرض، ونظرًا لأن من السهل تعريف هذا المجسم رياضيًا ببساطة، ولأن صيغته الرياضية بسيطة، فقد عكف علماء الجيوديزيا منذ بدايات القرن التاسع عشر على إيجاد المجسم الناقصي الأكثر دقة في تمثيل الأرض.
القطع الناقص Ellipse
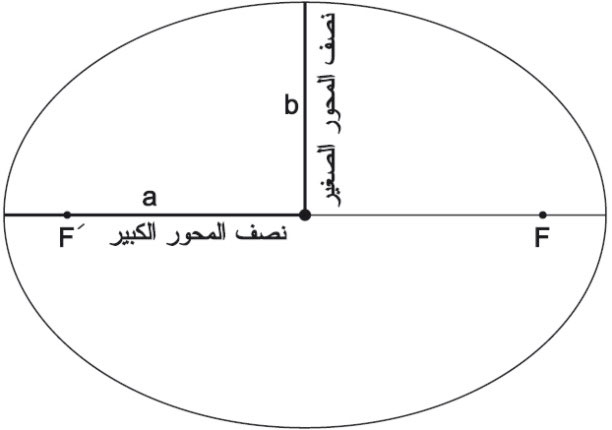
هو مجموعة نقاط المستوي التي مجموع بعديها عن نقطتين ثابتتين F/, F (الشكل 2)، في هذا المستوي، يساوي مقدارًا ثابتاً 2a، وهو طول المحور الكبير major axis.
تسمى كل من:
النقطتين F وF/ محرق القطع focus،
والنقطة O منتصف القطعة FF/ هي مركز القطع center،
وc طول القطعة المستقيمة OF يدعى البعد المحرقي،

تدعى التباعد المركزي eccentricity،

يدعى التسطح flattening.
وبين عناصر القطع a وc وb (نصف طول محوره الصغير) توجد العلاقة:

وهذا يعني أن معرفة العنصرين a وe فقط يكفي لتحديد بقية العناصر.
إذا كانت a = b فإن القطع يصبح دائرة، وتكون e = f = 0. أما إذا اقتربت b من الصفر فإن e وf تقتربان من الواحد، والقطع يتناهى إلى قطعة مستقيمة. أي إنه إذا بقيت قيمة a ثابتة وتناقصت قيمة b، فإن f وe تتزايدان مع تناقص قيمة b. مما يعني أنه كلما ازداد الفرق بين a وb ازداد التسطح وازداد التباعد المركزي.
مثال (1): قطع ناقص طول نصف محوره الكبير a = 5، طول نصف محوره الصغير b = 4:
ينتج أن التباعد المركزي له هو:.


مثال (2) : قطع ناقص عرف منه: طول نصف محوره الكبير a = 13، والتباعد المركزي له هو e = 0.923:
ينتج أن طول نصف محوره الصغير b = 5 والتسطح = 0.6154 = 13/ 8 تقريباً.
مثال (3): قطع ناقص طول نصف محوره الكبير a = 145: والتسطح = 0.883 = 145/ 128 تقريباً.
ينتج أن طول نصف محوره الصغير b = 17، والتباعد المركزي له هو e =0.993.
إحداثيات نقطة في الفضاء
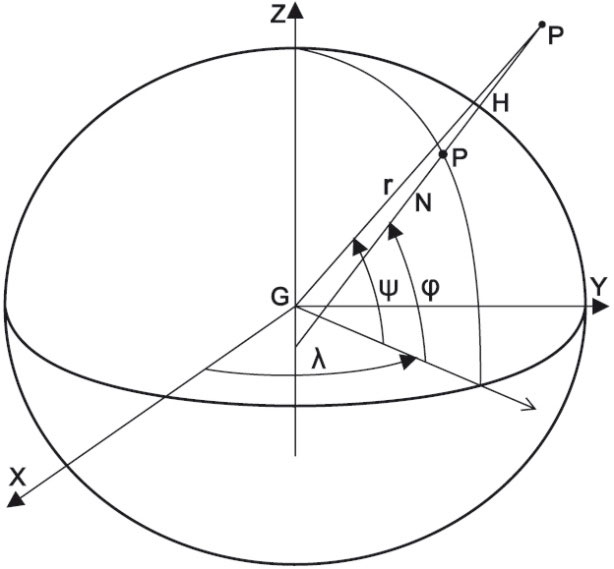
إذا نسب الفضاء إلى ثلاثية إحداثية متعامدة مباشرة GXYZ، حيث G هو مركز ثقل الأرض (مركز المجسم الناقصي المرجعي)، المحور GZ محور دوران الأرض، (حامل المحور الصغير، ذي الطول b2b، للمجسم )، المحوران GY, GX يقعان في مستوي الدائرة الاستوائية. المحور GX يقطع خط الطول المار بمدينة غرينتش Greenwich.
إذا كانت P نقطة من الفضاء (الشكل 3)، إحداثياتها (x, y, z) فإن:
x = (N+H) cosj cosλ = r cosψ cosλ
y = (N+H) cosj sinλ = r cosψ sinλ
z = [N (1- e2) +H] sinj = r sinψ
حيث H هو ارتفاع p عن سطح الأرض p (بعد p عن المجسم الناقصي)، λ خط الطول، j خط العرض، r طول GP و

ومعادلة المجسم الناقصي المرجعي لهذه الجملة الإحداثية هي:

تطور مجسم القطع الناقص المرجع
استمر علماء الجيوديزيا في السعي للوصول إلى تحديد طول نصف المحور الكبير a (نصف قطر دائرة خط الاستواء للأرض) لمجسم القطع الناقص المرجع، ومقدار تسطحه f، أو قيمة تباعده المركزي e. وقد تباينت القيم بتباين المؤسسات التي يعمل فيها هؤلاء العلماء، كما جرى عليها بعض التعديلات على مر السنين، والجدول (1) يبين بعض هذه التغيرات.
أنور توفيق اللحام
Reference ellipsoid - Ellipsoïde de référence
مجسم القطع الناقص
مجسم القطع الناقص (المرجع) أو المجسم الناقصي المرجعي reference ellipsoid هو سطح فراغي دوراني، ناتج من دوران قطع ناقص - معرف رياضيًا تعريفاً مناسباً - حول محوره الصغير، بحيث يكون المجسم أقرب ما يمكن إلى الشكل الحقيقي للأرض. ترسم عليه شبكة جيوديزية، تساعد على تعيين إحداثيات نقطة ما باستخدام هذه الشبكة.
سطح الأرض
إن وجه الأرض لا يمثل سطحًا فراغيًا منتظماً، إلا في أجزاء منه، حيث يمكن عدّ المحيطات سطوحًا منتظمة نوعاً ما، في حين التضاريس من جبال وأودية تشير إلى وجود تغيرات شاقولية كبيرة بينها على وجه الأرض فكان من المستحيل على علماء الجيوديزيا Geodesy - (وهو فرع من الرياضيات التطبيقية يهتم بدراسة الأرض، شكلها وأبعادها) - إعطاء نموذج رياضي مبسط ودقيق لسطح الأرض.
 |
|
| الشكل (1) |
إن الحاجة ماسة لاتخاذ نموذج رياضي للأرض، حتى يمكن تحديد موضع نقطة ما - على الأرض أو خارجها - بإحداثيات دقيقة، اعتمادًا على خطوط طول وخطوط عرض وارتفاعات محددة بدقة. ولأن سطح مجسم القطع الناقص هو تمثيل أقرب ما يكون لحقيقة وجه الأرض، ونظرًا لأن من السهل تعريف هذا المجسم رياضيًا ببساطة، ولأن صيغته الرياضية بسيطة، فقد عكف علماء الجيوديزيا منذ بدايات القرن التاسع عشر على إيجاد المجسم الناقصي الأكثر دقة في تمثيل الأرض.
القطع الناقص Ellipse
 |
|
| الشكل (2) |
تسمى كل من:
النقطتين F وF/ محرق القطع focus،
والنقطة O منتصف القطعة FF/ هي مركز القطع center،
وc طول القطعة المستقيمة OF يدعى البعد المحرقي،

تدعى التباعد المركزي eccentricity،

يدعى التسطح flattening.
وبين عناصر القطع a وc وb (نصف طول محوره الصغير) توجد العلاقة:

وهذا يعني أن معرفة العنصرين a وe فقط يكفي لتحديد بقية العناصر.
إذا كانت a = b فإن القطع يصبح دائرة، وتكون e = f = 0. أما إذا اقتربت b من الصفر فإن e وf تقتربان من الواحد، والقطع يتناهى إلى قطعة مستقيمة. أي إنه إذا بقيت قيمة a ثابتة وتناقصت قيمة b، فإن f وe تتزايدان مع تناقص قيمة b. مما يعني أنه كلما ازداد الفرق بين a وb ازداد التسطح وازداد التباعد المركزي.
مثال (1): قطع ناقص طول نصف محوره الكبير a = 5، طول نصف محوره الصغير b = 4:
ينتج أن التباعد المركزي له هو:.


مثال (2) : قطع ناقص عرف منه: طول نصف محوره الكبير a = 13، والتباعد المركزي له هو e = 0.923:
ينتج أن طول نصف محوره الصغير b = 5 والتسطح = 0.6154 = 13/ 8 تقريباً.
مثال (3): قطع ناقص طول نصف محوره الكبير a = 145: والتسطح = 0.883 = 145/ 128 تقريباً.
ينتج أن طول نصف محوره الصغير b = 17، والتباعد المركزي له هو e =0.993.
إحداثيات نقطة في الفضاء
إذا نسب الفضاء إلى ثلاثية إحداثية متعامدة مباشرة GXYZ، حيث G هو مركز ثقل الأرض (مركز المجسم الناقصي المرجعي)، المحور GZ محور دوران الأرض، (حامل المحور الصغير، ذي الطول b2b، للمجسم )، المحوران GY, GX يقعان في مستوي الدائرة الاستوائية. المحور GX يقطع خط الطول المار بمدينة غرينتش Greenwich.
 |
|
| الشكل (3) |
x = (N+H) cosj cosλ = r cosψ cosλ
y = (N+H) cosj sinλ = r cosψ sinλ
z = [N (1- e2) +H] sinj = r sinψ
حيث H هو ارتفاع p عن سطح الأرض p (بعد p عن المجسم الناقصي)، λ خط الطول، j خط العرض، r طول GP و

ومعادلة المجسم الناقصي المرجعي لهذه الجملة الإحداثية هي:

تطور مجسم القطع الناقص المرجع
استمر علماء الجيوديزيا في السعي للوصول إلى تحديد طول نصف المحور الكبير a (نصف قطر دائرة خط الاستواء للأرض) لمجسم القطع الناقص المرجع، ومقدار تسطحه f، أو قيمة تباعده المركزي e. وقد تباينت القيم بتباين المؤسسات التي يعمل فيها هؤلاء العلماء، كما جرى عليها بعض التعديلات على مر السنين، والجدول (1) يبين بعض هذه التغيرات.
| مجسم | السنة | الرمز | نصف المحور الكبير a (متر) | التسطح |
| النظام الجيوديزي المرجعي | 1980 | GRS80 | 6 378 137 | 0033528. 0 |
| النظام الجيوديزي العالمي | 1972 | WGS72 | 6 378 135 | 0033528. 0 |
| النظام الجيوديزي المرجعي | 1967 | GRS67 | 6 378 160 | 0033529. 0 |
| كراسوفسكي Krassovski | 1942 | 6 378 245 | 0033523. 0 | |
| الدولي international | 1924 | 6 378 388 | 0033670. 0 | |
| كلارك Clark | 1866 | 6 378 206 | 0033901. 0 | |
| بسل Bessel | 1842 | 6 377 397 | 0033428. 0 | |
| * GRS اختصار العبارة Geodetic Refernce Systen لنظام الجيوديزي المرجعي. | ||||
| ** WGS اختصارالعبارة World Geodetic Systen | ||||
أنور توفيق اللحام
