تويت
حساب (علم)
Arithmetic - Arithmétique
الحساب ( علم ـ)
الحسابarithmetic هو علم الأعداد وموضوعه العدد، وهو ما يقع في العدّ. العدّ هو إحصاء الأشياء المتماثِلة.
وفي علم الحساب جانبان: جانب نظري يعالج الأعداد وخواصها، وجانب عملي يتناول العمليات عليها.
أنظمة العد المكتوبة
احتاج الإنسان منذ القدم في معاملاته إلى تقييد الأعداد، فاستنبط طرقاً مختلفة لكتابة الأعداد، وأنظمةً مختلفة للعد.
وقد عثر على تقويم مدوّن عند السومريين يعود إلى عام 5700ق.م، وَوُجِدَ ما يدل على أنهم استخدموا النظام الستيني في العد.
وهذه بعض الطرق التاريخية في كتابة الأعداد:
1- عند المصريين (نحو عام 3000ق.م): تعارف المصريون على كتابة الواحد بشكل خط رأسي قائمٍ | والاثنين خطين ||، وهكذا. وجعلوا العشرة باباً مقنطراً Ç، وهي تتكرر بتكرر العشرات، وجعلوا للمئة علامة e وهكذا.
ودونوا الأعداد الكبيرة بطريقة بسيطة، فجعلوا مثلاً العلامة الدالة على المليون رجلاً راكعاً.
وكان عندهم رمز للكسر العادي، فوضعوا علامة بيضوية فوق العدد للدلالة على مقلوبه، وجعلوا الكسرَ الذي بسطه أكبر من الواحد مجموع بسوطٍ بسط كل منها 1، فكتبوا الكسر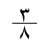
بالشكل 
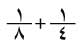والكسر 
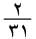بالشكل 
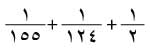وكان عندهم علامة للجذر التربيعي هي ┌.
2- عند البابليين: اعتمد البابليون العلامة المسمارية
للدلالة على الواحد، وهي تتكرر مع تكرار الواحدات، واعتمدوا للعشرة علامة هي 
، وهي تتكرر بتكرر العشرات وللمئة خطين أحدهما عمودي والآخر أفقي إلى اليمين، ويلاحظ أن التدوين البابلي للأعداد شيءٌ من مَدْرَكِ الخانات.
استخدم البابليون نظام العد الستيني، وجعلوا علامة الستين هي Ñ، واستخدمت العلامة ذاتها للواحد أيضاً. وهكذا فالعدد 30 مثلاً يدل على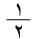
.
يكتب العدد في النظام الستيني بشكل مجموع قوى العدد 60، الذي يدعى أساس النظام، فالعدد (2،11،21،32) في النظام الستيني والذي يكتب بالترقيم البابلي بالشكل:
يعني 2 × 360 + 11 × 260 + 21 × 160 + 32 × 060
ويمكن أن يعني 2 × 260 + 11 × 160 + 21 × 060، ويعرف العدد المراد من القرينة، وهكذا يكون البابليون استخدموا نظام الفاصلة العائمة في حساباتهم.
وكان عند البابليين جداول للضرب والقسمة والتربيع والجذور التربيعية، ولم يستخدموا علامة للصفر بل كانوا يتركون فراغاً مكان الصفر.
3- عند اليونان: أخذ اليونان الأحرف الهجائية لتدوين الأعداد من الفينيقيين، وزادوا فيها فجعلوا الأحرف الأبجدية العشرة الأولى دالة على الآحاد، والتي تليها على العشرات، وهكذا ... حتى الحرف λ الذي جعلوه دالاً على 900.
ثم وضعوا فاصلة أمام الحروف للدلالة على الألوف، فجعلوا مثلاً θ دالة على 9000 ثم جعلوا الحرف M دالاً على 10000. ولم يستخدم اليونانيون علامةً للصفر، وقد استخدموا طريقة المصريين في التعبير عن الكسور.
4- عند الرومان: كان للرومان تدوين مستقلٌ للأعداد، وكان مزيجاً عرفياً من العلامات والأحرف. ومازال بعضها يستخدم اليوم في تدوين النتائج مثل:
X IX … V … III II I.
5- عند الهنود: جعل الهنود للترقيم علامات مستقلة، وهي التي تعرف الآن بالأعداد الهندية، ثم إنهم أوجدوا علامة للصفر. ولا يُعلم أنهم استفادوا من الأعداد التي وضعوها ولا من الصفر.
6- عند العرب: بقي العرب إلى صدر العصر العباسي يدونون الأعداد بالكلمات (فيقولون مثلاً أربعمئة وأربعة) أو بالحروف الهجائية، فكتبوا علامات الأعداد بالشكل:
واستخدموا الجمل للتعبير عن الأعداد الكبيرة.
وفي العصر العباسي أخذ العرب الأعداد (من ضمنها الصفر) من الهنود وسموها الأرقام الهندية، وسموا العمليات عليها الحساب الهندي، وجعلوا الصفر دالاً على الجزء الخالي من العدد، وظهرت الأرقام الهندية (والصفر) في كتب عربية أُلفت منذ 274هـ/787م. وابتكروا الخانات، فسَهُل بذلك حلّ المسائل الحسابية وتدوين الكسور العادية والعَشرية. وقد احتاجت الأعداد الجديدة إلى قرنين تقريباً لتبلغ إسبانيا ثم لتدخل أوربا.
استخدم الهنود والإغريق والعرب نظام العد العشري، ومازال مستخدماً لسهولته. ويكتب العدد في هذا النظام كمجموع قوى العدد 10، الذي يدعى أساس النظام العشري. ويحتاج هذا النظام إلى عشرة أرقام مختلفة هي (9،8،7،6،5،4،3،2،1،0)، للتعبير عن الأعداد. وكان العالم غياث الدين الكاشي من أوائل الرياضيين الذين استخدموا القوى السالبة في النظام العشري.
بعد التطور الهائل للحواسيب غدا نظام العد الثنائي الذي أساسه العدد 2 هو الأكثر ملاءمة، فهو يحتاج إلى رقمين فقط 1 يدل على مرور التيار و0 يدل على عدم مروره، وتكتب الأعداد في هذا النظام كمجموع قوى العدد 2، ثمّ دعت الحاجة لتكثيف هذا النظام فاستخدمت نظم عدٍّ أساسها 16 أو 64 أو غيرها من قـوى الـ2 .
العمليات على الأعداد
وتعني العمليات المرتبطة بالأعداد وهي: الجمع، التفريق، الضرب، القسمة، القوة، الجذر.
استخدم الإنسان القديم أصابعه للعد ولإجراء العمليات عليها، وحين صار لزاماً عليه أن يقوم بحسابات معقدة، بحث عن وسائل لتسهيل عمله، فاستخدم البابليون قبل آلاف السنين ألواح الغبار لتساعدهم في سرعة إجراء العمليات، ثم طُور اللوح فأصبح مَحْسَباً، واستمر التطور واستخدمت جداول عددية للعمليات الأساسية، ثم استخدمت الجداول اللوغاريتمية. واللوغاريتم ( الأسيس ) هو الأس الدال على المقدار الذي يجب أن ترفع إليه عدداً معيناً أكبر من الواحد (نسميه الأساس) كي نحصل على العدد المطلوب. وقد جدولت اللوغاريتمات لتستخدم في تسهيل العمل في المسائل التي تتضمن أعداداً كبيرة بأن يصبح الجمع والطرح في هذه المسائل يقومان مقام الضرب والقسمة.
ويعود الفضل إلى جون نابيير John Napier ت(1550- 1617م) الذي وضع أول جدول لوغاريتمي عام 1614م. لكن الفكرة الأساسية كانت لمعت في الذهن العربي، وذلك نحو سنة 210هـ/825م، حين ألف الحاسب سنان بن الفتح الحراني كتاب «الجمع والتفريق» شرح فيه الطريقة التي يمكن أن تحلّ بها المسائل القائمة على الضرب والقسمة بالجمع والطرح. وقد استطاع الرياضي ابن يونس المصري (399هـ/1008م) أن يوجد القانون المثلثاتي:
2 تحب س تحب ص = تحب (س + ص) + تحب (س - ص)، الذي استخدم عند علماء الفلك، قبل استخدام الجداول اللوغاريتمية لتحويل عمليات الضرب إلى عمليات جمع. واستمر التطور إلى أن تمكن الإنسان من صنع حواسيب تُجري العمليات المعقدة بسرعة تفوق كل تصور.
الحساب النظري
ويعالج الأعداد وخواصها.
استخدم الإنسان الأعداد منذ ما يزيد على 5000 سنة دون أن يفكر بدراسة الأعداد ذاتها وخواصها، ويمكن القول إن الاهتمام العلمي بالأعداد وخواصها كان ابتداءً عند اليونان في عهد فيثاغورث Pythagoras نحو 600ق.م، الذي زار بابل ومصر والهند لأخذ آخر ما توصل إليه العلم.
ويعد فيثاغورث أول من صنف الأعداد بحسب خواصها وعرف الأعداد الزوجيةeven numbers هي6،4،2...... والأعداد الفرديةodd numbers هي 7،5،3،1،..... والأعداد الأولية prime numbers هي 7،5،3،2... (العدد الأولي: هو عدد صحيح أكبر من الواحد لايقبل القسمة إلا على نفسه وعلى الواحد)، والأعداد المركبة (غير الأولية) 8،6،4 ....
ثم ربط الأعداد بالهندسة فعرف الأعداد المثلثة
والأعداد المضلَّعة. وأوجد علماء مدرسته ثلاثيات فيثاغورث (وهي الأعداد الصحيحة الثلاثة التي تمثل أطوال أضلاع مثلث قائم الزاوية)، وعرفوا الأعداد الكاملة (وهي الأعداد التي مجموع قواسمها يساوي العدد نفسه فالعدد 6، الذي مجموع قواسمه 1، 2، 3 يساوي 6،عدد كامل)، والأعداد المتحابة (مجموع قواسم أي منهما يساوي العدد الآخر كالعددين 220 و284).
بعد وفاة فيثاغورث بـ 200 سنة أنشئت جامعة في الإسكندرية، وذلك في القرن الثالث قبل الميلاد، وكان من أهم أعضائها إقليدس Euclid الذي ألف سنة 300ق.م تقريباً كتاب «الأصول» الذي يحوي 13 مقالة، تبحث ثلاث منها في نظرية الأعداد، أثبت فيها أن مجموعة الأعداد الأولية غير منتهية، وأوجد طريقة لحساب القاسم المشترك الأعظم لعددين، وطريقة لتحليل الأعداد إلى عواملها الأولية، وبحث عن الأعداد الكاملة، وأثبت أن العدد الزوجي الكامل هو من الشكل 2ب-1 (2ب -1 ) حيث ب و2 ب-1 أعداد أولية.
وقد مر 2000 عام قبل أن يثبت العالم أولر Leonhard Euler ت(1707-1783م) عكس هذه المبرهنة، ولم يعرف حتى الآن إن كان هناك عدد فردي كامل.
مضت 500 سنة بعد إقليدس دون أن يطرأ تطور يذكر على نظرية الأعداد إلى أن ظهر العالم اليوناني ديوفانتس الاسكندري Diophantus of Alexandria نحو عام 250م، وهو أول عالم يوناني استخدم الرموز الجبرية في المعادلات، وأوجد حلولاً صحيحة لمعادلات بمجهولين أو ثلاثة مجاهيل، ويسمى هذا النوع من المعادلات الآن معادلات ديوفانتس، وهي التي يسميها العرب المعادلات السيّالة، ولم يبحث ديوفانتس في جميع حلول المعادلة، بل كان يكتفي بإيجاد حل واحد وبطريقة خاصة. كما بحث في خواص الأعداد الصحيحة ولم يتعرض للأعداد السالبة.
وبعد ديوفانتس انتقل هذا العلم إلى العرب الذين عملوا على نقله وتهذيبه وتطويره.
اهتم الرياضيون العرب اهتماماً فائقاً بكتاب «الأصول» لإقليدس، فكان من الذين اختصروه العالم ابن سينا (428هـ). ومن الذين حرروه نصير الدين الطوسي (672هـ) ومن الذين شرحوا الكتاب بكامله وحلوا شكوكه الحسن بن الهيثم (432هـ).
ومرت مئات السنين قبل أن تشارك أوربة في تطوير علم الحساب حتى ظهر في القرن السابع عشر للميلاد الرياضي الفرنسي بيير دي فيرما Pierre de Fermat ت(1601-1665م) الذي استفاد من أعمال ديوفانتس وطوّرها ووضع مبرهنات عدة أثبت بعضها. وقد أثبت أن كل عدد أولي فردي يمكن أن يكتب بطريقة وحيدة كفرق عددين مربعين، وأن كل عدد صحيح هو إما عدد مثلثي أو هو مجموع عددين أو ثلاثة أعداد مثلثة، كما بين أن كل عـدد أولـي من الشـكل 4 ن + 1 هو مجموع مربعي عددين مثل 17 = 21 + 24، 13 = 22 + 23.
وضع فيرما عام 1640م الدعوى الهامة التي تعرف بمبرهنة فيرما الصغرى، التي تنص على أنه إذا كان ب عدداً أولياً، وكان حـ عدداً صحيحاً وكان (ب،حـ) =1، أي، ب وحـ أوليان نسبياً، كان العدد (جـب-1 -1) يقبل القسمة على ب ولم تثبت هذه الدعوى إلا بعد قرابة مئة عام، وكان أويلر هو أول من نشر برهاناً لها عام 1736م.
ثم وضع فيرما الدعوى التي تعرف بمبرهنة فيرما الكبرى (أو الأخيرة) وهي أنه لاتوجد أي أعداد صحيحة موجبة ن، س، ع، ص تحقق المساواة سن + عن = صن، بافتراض أن ن < 2.
وكتب فيرما على هامش كتاب الحساب لديوفانتس الذي كان يدرسه أنه توصل إلى برهان هذه الدعوى، لكن الهامش لايتسع لكتابتها. وقد استعصت هذه الدعوى على الحل، وأربكت العقول مدة تتجاوز ثلاثة قرون، وفي عام 1993 قدم العالم أندرو وايلز Androw Wiles من جامعة برنستون برهاناً يقع في 200 صفحة. وبعد تفحص العلماء للحل تبين أن هناك خللاً في إحدى خطوات البرهان. لذا دأب وايلز على تصحيح الخلل بالتعاون مع ريتشارد تايلر Richald Taylor. ومن المعتقد عند معظم الرياضيين المهتمين بالموضوع أن البرهان المقدم عام 1994، الذي اعتمد فيه على الكثير من أحدث الأفكار في فروع عدة من الرياضيات صحيح.
وتوقع فيرما أن تكون الأعداد التي تكتب على الصورة 2 2ن + 1 ون عدد صحيح £ 0 هي أعداد أولية، وقد تمكن أويلر عام 1732م من إثبـات أن العـدد 2 2ن + 1 غير أولي، ويقال أن هذا هوالحدس الذي أخطأ به فيرما.
بعد فيرما لمعت أسماء علماء تابعوا العمل في نظرية الأعداد. ومن المسائل التي استقطبت اهتمام الكثيرين هي مسألة توزع الأعداد الأولية، فعُرفت الـدالـة π(س) = عدد الأعداد الأولية ب التي تحقق العلاقة س £ ب £ 2.
وقد لاحظ كل من العالمين لوجاندرA.M.Legendre ت(1752- 1833 م) وغوص C.F.Gauss ت(1777- 1855م)، كـل على حـده، أن نسـبة الـدالـة π(س) إلى الدالة س/لع س تقترب من الواحد في حال القيم الكبيرة لـ س، ولم يفلح أيّ منهما في إثبات وجود نهاية لهذه النسبة.
وفي عام 1851م أثبت العالم الروسي تشيبيتشيف P.L.Tchebychev ت(1821-1894 م ) أنّه إن كان لهذه النسبة نهاية فهذه النهاية تساوي 1.
وفي عام 1896م أفلح كلُّ من بوسان C.J.V.Poussin وآدامار G.Hadamard من إثبات وجود هذه النهاية، وفي عام 1949م نشر سلبرغ Selberg برهاناً بسيطاً أثار ضجة علمية.
من القضايا المثيرة في نظرية الأعداد تخمين غولد باخC.Goldbach ت(1690- 1764م) الذي خمّن فيه أنّ كل عدد زوجي £ 4 هو مجموع عددين أوليين. وقد جربت الأعداد حتى العدد 33 × 10 ووجد أنّ كل عدد زوجي £ 6 هو مجموع عددين أوليين فرديين مختلفين.
وفي عام 1948م أثبت الرياضي رينيه A.Renye وجود عدد ب بحيث إنّ أي عدد صحيح زوجي كبير ن يمكن أن يكتب كمجموع عدد أولي وعدد آخر عدد عوامله الأولية لايتجاوز ب.
وفي عام 1966م أثبت العالم تشين غين ران Chen Ging-Run أنّ العدد ب ³ 2. ويمكن القول إن نظرية الأعداد ما زالت تحوي المئات من المسائل المفتوحة، وأن عدد المسائل الجديدة التي ليس لها حل أكثر من عدد المسائل المفتوحة التي يعثر لها على حل.
إن موضوع نظرية الأعداد هو العدد الطبيعي. فما هي مجموعة الأعداد الطبيعية ؟
لقد نشر جيوسيبي بيانو Giusepp Peano ت(1858-1932م) مقالةً عام 1889م أعطى فيها مفهوم مجموعة الأعداد الطبيعية (الأعداد الصحيحة غير السالبة) وفق مسلَّمات سميت مسلَّمات بيانو.
بعض كبار علماء الحساب
1- أبو علي الحسن بن الحسن بن الهيثم، ولد سنة 354 هـ/965م في البصرة، وتوفي في القاهرة سنة 432هـ/ 1041م. وقد ترك عدداً كبيراً من الكتب والمقالات في معظم فروع العلوم وفي الطب، ترجم الكثير منها إلى لغات أجنبية متعددة. ووجد لابن الهيثم 66 عملاً رياضياً تميزت بالمنهجية العلمية. ومن أهم ما صنف في علم الحساب كتاب: «في حل شكوك كتاب إقليدس في الأصول وشرح معانيه»، وقدم في هذا الكتاب براهين فاق الكثير منها البراهين التي قدمها إقليدس وحلّ الشكوك حول بعض مسائل إقليدس وشرحها.
2- جمشيد بن مسعود الملقب بغياث الدين الكاشي: ولد في المدينة الإيرانية كاشان، وورد أنه توفي نحو 845هـ/1436م. لم يكن الكاشي رياضياً فحسب بل كان فلكياً وطبيباً. وهو أول من تسلم إدارة مرصد ألوغ بك في سمرقند. للكاشي مؤلفات كثيرة في علوم رياضية متنوعة، آخر مؤلفاته رسالة «مفتاح الحساب» التي أنجزها في سمرقند سنة 1427م، وتعد هذه الرسالة موسوعة لرياضيات ذلك الزمان لما ورد فيها من مسائل مبتكرة تتعلق بأصول حساب الصحاح بالأرقام الهندية والحسابات التقريبية، وشرح للكسور العشرية. ثم إنه دوَّن في هذه الرسالة طريقة لاستخراج الجذور من أيّ دليل كان، وبحث في تحويل الأعداد الستينية إلى عشرية، وتكلم فيها على مراتب الأعداد (الخانات) وغير ذلك.
3- سنان بن الفتح الحراني (210هـ/825م)، كان رياضياً من أشهر مؤلفاته كتاب «الجمع والتفريق». وقد شرح فيه الطريقة التي يمكن أن تحل بها المسائل القائمة على الضرب والقسمة بالجمع والطرح.
ألف أيضاً كتاب «المكعبات»، شرح فيه طريقة توزيع الأعداد وتصنيفها، إضافة إلى جذورها وحساب مكعباتها.
4- تشيبيتشيف P.L.Tchebychev ت(1821–1894م): هو العالم الروسي الشهير الذي برع في نظرية الأعداد والتحليل والاحتمالات والميكانيك.
دعد الحسيني
Arithmetic - Arithmétique
الحساب ( علم ـ)
الحسابarithmetic هو علم الأعداد وموضوعه العدد، وهو ما يقع في العدّ. العدّ هو إحصاء الأشياء المتماثِلة.
وفي علم الحساب جانبان: جانب نظري يعالج الأعداد وخواصها، وجانب عملي يتناول العمليات عليها.
أنظمة العد المكتوبة
احتاج الإنسان منذ القدم في معاملاته إلى تقييد الأعداد، فاستنبط طرقاً مختلفة لكتابة الأعداد، وأنظمةً مختلفة للعد.
وقد عثر على تقويم مدوّن عند السومريين يعود إلى عام 5700ق.م، وَوُجِدَ ما يدل على أنهم استخدموا النظام الستيني في العد.
وهذه بعض الطرق التاريخية في كتابة الأعداد:
1- عند المصريين (نحو عام 3000ق.م): تعارف المصريون على كتابة الواحد بشكل خط رأسي قائمٍ | والاثنين خطين ||، وهكذا. وجعلوا العشرة باباً مقنطراً Ç، وهي تتكرر بتكرر العشرات، وجعلوا للمئة علامة e وهكذا.
ودونوا الأعداد الكبيرة بطريقة بسيطة، فجعلوا مثلاً العلامة الدالة على المليون رجلاً راكعاً.
وكان عندهم رمز للكسر العادي، فوضعوا علامة بيضوية فوق العدد للدلالة على مقلوبه، وجعلوا الكسرَ الذي بسطه أكبر من الواحد مجموع بسوطٍ بسط كل منها 1، فكتبوا الكسر
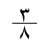بالشكل 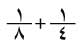والكسر 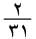بالشكل 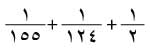وكان عندهم علامة للجذر التربيعي هي ┌.2- عند البابليين: اعتمد البابليون العلامة المسمارية
للدلالة على الواحد، وهي تتكرر مع تكرار الواحدات، واعتمدوا للعشرة علامة هي ، وهي تتكرر بتكرر العشرات وللمئة خطين أحدهما عمودي والآخر أفقي إلى اليمين، ويلاحظ أن التدوين البابلي للأعداد شيءٌ من مَدْرَكِ الخانات.استخدم البابليون نظام العد الستيني، وجعلوا علامة الستين هي Ñ، واستخدمت العلامة ذاتها للواحد أيضاً. وهكذا فالعدد 30 مثلاً يدل على
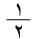.يكتب العدد في النظام الستيني بشكل مجموع قوى العدد 60، الذي يدعى أساس النظام، فالعدد (2،11،21،32) في النظام الستيني والذي يكتب بالترقيم البابلي بالشكل:
يعني 2 × 360 + 11 × 260 + 21 × 160 + 32 × 060
ويمكن أن يعني 2 × 260 + 11 × 160 + 21 × 060، ويعرف العدد المراد من القرينة، وهكذا يكون البابليون استخدموا نظام الفاصلة العائمة في حساباتهم.
وكان عند البابليين جداول للضرب والقسمة والتربيع والجذور التربيعية، ولم يستخدموا علامة للصفر بل كانوا يتركون فراغاً مكان الصفر.
3- عند اليونان: أخذ اليونان الأحرف الهجائية لتدوين الأعداد من الفينيقيين، وزادوا فيها فجعلوا الأحرف الأبجدية العشرة الأولى دالة على الآحاد، والتي تليها على العشرات، وهكذا ... حتى الحرف λ الذي جعلوه دالاً على 900.
ثم وضعوا فاصلة أمام الحروف للدلالة على الألوف، فجعلوا مثلاً θ دالة على 9000 ثم جعلوا الحرف M دالاً على 10000. ولم يستخدم اليونانيون علامةً للصفر، وقد استخدموا طريقة المصريين في التعبير عن الكسور.
4- عند الرومان: كان للرومان تدوين مستقلٌ للأعداد، وكان مزيجاً عرفياً من العلامات والأحرف. ومازال بعضها يستخدم اليوم في تدوين النتائج مثل:
X IX … V … III II I.
5- عند الهنود: جعل الهنود للترقيم علامات مستقلة، وهي التي تعرف الآن بالأعداد الهندية، ثم إنهم أوجدوا علامة للصفر. ولا يُعلم أنهم استفادوا من الأعداد التي وضعوها ولا من الصفر.
6- عند العرب: بقي العرب إلى صدر العصر العباسي يدونون الأعداد بالكلمات (فيقولون مثلاً أربعمئة وأربعة) أو بالحروف الهجائية، فكتبوا علامات الأعداد بالشكل:
واستخدموا الجمل للتعبير عن الأعداد الكبيرة.
وفي العصر العباسي أخذ العرب الأعداد (من ضمنها الصفر) من الهنود وسموها الأرقام الهندية، وسموا العمليات عليها الحساب الهندي، وجعلوا الصفر دالاً على الجزء الخالي من العدد، وظهرت الأرقام الهندية (والصفر) في كتب عربية أُلفت منذ 274هـ/787م. وابتكروا الخانات، فسَهُل بذلك حلّ المسائل الحسابية وتدوين الكسور العادية والعَشرية. وقد احتاجت الأعداد الجديدة إلى قرنين تقريباً لتبلغ إسبانيا ثم لتدخل أوربا.
استخدم الهنود والإغريق والعرب نظام العد العشري، ومازال مستخدماً لسهولته. ويكتب العدد في هذا النظام كمجموع قوى العدد 10، الذي يدعى أساس النظام العشري. ويحتاج هذا النظام إلى عشرة أرقام مختلفة هي (9،8،7،6،5،4،3،2،1،0)، للتعبير عن الأعداد. وكان العالم غياث الدين الكاشي من أوائل الرياضيين الذين استخدموا القوى السالبة في النظام العشري.
بعد التطور الهائل للحواسيب غدا نظام العد الثنائي الذي أساسه العدد 2 هو الأكثر ملاءمة، فهو يحتاج إلى رقمين فقط 1 يدل على مرور التيار و0 يدل على عدم مروره، وتكتب الأعداد في هذا النظام كمجموع قوى العدد 2، ثمّ دعت الحاجة لتكثيف هذا النظام فاستخدمت نظم عدٍّ أساسها 16 أو 64 أو غيرها من قـوى الـ2 .
العمليات على الأعداد
وتعني العمليات المرتبطة بالأعداد وهي: الجمع، التفريق، الضرب، القسمة، القوة، الجذر.
استخدم الإنسان القديم أصابعه للعد ولإجراء العمليات عليها، وحين صار لزاماً عليه أن يقوم بحسابات معقدة، بحث عن وسائل لتسهيل عمله، فاستخدم البابليون قبل آلاف السنين ألواح الغبار لتساعدهم في سرعة إجراء العمليات، ثم طُور اللوح فأصبح مَحْسَباً، واستمر التطور واستخدمت جداول عددية للعمليات الأساسية، ثم استخدمت الجداول اللوغاريتمية. واللوغاريتم ( الأسيس ) هو الأس الدال على المقدار الذي يجب أن ترفع إليه عدداً معيناً أكبر من الواحد (نسميه الأساس) كي نحصل على العدد المطلوب. وقد جدولت اللوغاريتمات لتستخدم في تسهيل العمل في المسائل التي تتضمن أعداداً كبيرة بأن يصبح الجمع والطرح في هذه المسائل يقومان مقام الضرب والقسمة.
ويعود الفضل إلى جون نابيير John Napier ت(1550- 1617م) الذي وضع أول جدول لوغاريتمي عام 1614م. لكن الفكرة الأساسية كانت لمعت في الذهن العربي، وذلك نحو سنة 210هـ/825م، حين ألف الحاسب سنان بن الفتح الحراني كتاب «الجمع والتفريق» شرح فيه الطريقة التي يمكن أن تحلّ بها المسائل القائمة على الضرب والقسمة بالجمع والطرح. وقد استطاع الرياضي ابن يونس المصري (399هـ/1008م) أن يوجد القانون المثلثاتي:
2 تحب س تحب ص = تحب (س + ص) + تحب (س - ص)، الذي استخدم عند علماء الفلك، قبل استخدام الجداول اللوغاريتمية لتحويل عمليات الضرب إلى عمليات جمع. واستمر التطور إلى أن تمكن الإنسان من صنع حواسيب تُجري العمليات المعقدة بسرعة تفوق كل تصور.
الحساب النظري
ويعالج الأعداد وخواصها.
استخدم الإنسان الأعداد منذ ما يزيد على 5000 سنة دون أن يفكر بدراسة الأعداد ذاتها وخواصها، ويمكن القول إن الاهتمام العلمي بالأعداد وخواصها كان ابتداءً عند اليونان في عهد فيثاغورث Pythagoras نحو 600ق.م، الذي زار بابل ومصر والهند لأخذ آخر ما توصل إليه العلم.
ويعد فيثاغورث أول من صنف الأعداد بحسب خواصها وعرف الأعداد الزوجيةeven numbers هي6،4،2...... والأعداد الفرديةodd numbers هي 7،5،3،1،..... والأعداد الأولية prime numbers هي 7،5،3،2... (العدد الأولي: هو عدد صحيح أكبر من الواحد لايقبل القسمة إلا على نفسه وعلى الواحد)، والأعداد المركبة (غير الأولية) 8،6،4 ....
ثم ربط الأعداد بالهندسة فعرف الأعداد المثلثة
 |
| والأعداد المربعة |
 |
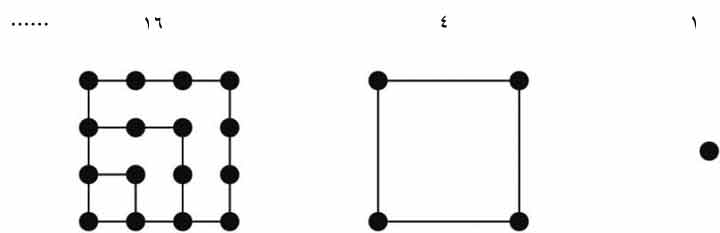بعد وفاة فيثاغورث بـ 200 سنة أنشئت جامعة في الإسكندرية، وذلك في القرن الثالث قبل الميلاد، وكان من أهم أعضائها إقليدس Euclid الذي ألف سنة 300ق.م تقريباً كتاب «الأصول» الذي يحوي 13 مقالة، تبحث ثلاث منها في نظرية الأعداد، أثبت فيها أن مجموعة الأعداد الأولية غير منتهية، وأوجد طريقة لحساب القاسم المشترك الأعظم لعددين، وطريقة لتحليل الأعداد إلى عواملها الأولية، وبحث عن الأعداد الكاملة، وأثبت أن العدد الزوجي الكامل هو من الشكل 2ب-1 (2ب -1 ) حيث ب و2 ب-1 أعداد أولية.
وقد مر 2000 عام قبل أن يثبت العالم أولر Leonhard Euler ت(1707-1783م) عكس هذه المبرهنة، ولم يعرف حتى الآن إن كان هناك عدد فردي كامل.
مضت 500 سنة بعد إقليدس دون أن يطرأ تطور يذكر على نظرية الأعداد إلى أن ظهر العالم اليوناني ديوفانتس الاسكندري Diophantus of Alexandria نحو عام 250م، وهو أول عالم يوناني استخدم الرموز الجبرية في المعادلات، وأوجد حلولاً صحيحة لمعادلات بمجهولين أو ثلاثة مجاهيل، ويسمى هذا النوع من المعادلات الآن معادلات ديوفانتس، وهي التي يسميها العرب المعادلات السيّالة، ولم يبحث ديوفانتس في جميع حلول المعادلة، بل كان يكتفي بإيجاد حل واحد وبطريقة خاصة. كما بحث في خواص الأعداد الصحيحة ولم يتعرض للأعداد السالبة.
وبعد ديوفانتس انتقل هذا العلم إلى العرب الذين عملوا على نقله وتهذيبه وتطويره.
اهتم الرياضيون العرب اهتماماً فائقاً بكتاب «الأصول» لإقليدس، فكان من الذين اختصروه العالم ابن سينا (428هـ). ومن الذين حرروه نصير الدين الطوسي (672هـ) ومن الذين شرحوا الكتاب بكامله وحلوا شكوكه الحسن بن الهيثم (432هـ).
ومرت مئات السنين قبل أن تشارك أوربة في تطوير علم الحساب حتى ظهر في القرن السابع عشر للميلاد الرياضي الفرنسي بيير دي فيرما Pierre de Fermat ت(1601-1665م) الذي استفاد من أعمال ديوفانتس وطوّرها ووضع مبرهنات عدة أثبت بعضها. وقد أثبت أن كل عدد أولي فردي يمكن أن يكتب بطريقة وحيدة كفرق عددين مربعين، وأن كل عدد صحيح هو إما عدد مثلثي أو هو مجموع عددين أو ثلاثة أعداد مثلثة، كما بين أن كل عـدد أولـي من الشـكل 4 ن + 1 هو مجموع مربعي عددين مثل 17 = 21 + 24، 13 = 22 + 23.
وضع فيرما عام 1640م الدعوى الهامة التي تعرف بمبرهنة فيرما الصغرى، التي تنص على أنه إذا كان ب عدداً أولياً، وكان حـ عدداً صحيحاً وكان (ب،حـ) =1، أي، ب وحـ أوليان نسبياً، كان العدد (جـب-1 -1) يقبل القسمة على ب ولم تثبت هذه الدعوى إلا بعد قرابة مئة عام، وكان أويلر هو أول من نشر برهاناً لها عام 1736م.
ثم وضع فيرما الدعوى التي تعرف بمبرهنة فيرما الكبرى (أو الأخيرة) وهي أنه لاتوجد أي أعداد صحيحة موجبة ن، س، ع، ص تحقق المساواة سن + عن = صن، بافتراض أن ن < 2.
وكتب فيرما على هامش كتاب الحساب لديوفانتس الذي كان يدرسه أنه توصل إلى برهان هذه الدعوى، لكن الهامش لايتسع لكتابتها. وقد استعصت هذه الدعوى على الحل، وأربكت العقول مدة تتجاوز ثلاثة قرون، وفي عام 1993 قدم العالم أندرو وايلز Androw Wiles من جامعة برنستون برهاناً يقع في 200 صفحة. وبعد تفحص العلماء للحل تبين أن هناك خللاً في إحدى خطوات البرهان. لذا دأب وايلز على تصحيح الخلل بالتعاون مع ريتشارد تايلر Richald Taylor. ومن المعتقد عند معظم الرياضيين المهتمين بالموضوع أن البرهان المقدم عام 1994، الذي اعتمد فيه على الكثير من أحدث الأفكار في فروع عدة من الرياضيات صحيح.
وتوقع فيرما أن تكون الأعداد التي تكتب على الصورة 2 2ن + 1 ون عدد صحيح £ 0 هي أعداد أولية، وقد تمكن أويلر عام 1732م من إثبـات أن العـدد 2 2ن + 1 غير أولي، ويقال أن هذا هوالحدس الذي أخطأ به فيرما.
بعد فيرما لمعت أسماء علماء تابعوا العمل في نظرية الأعداد. ومن المسائل التي استقطبت اهتمام الكثيرين هي مسألة توزع الأعداد الأولية، فعُرفت الـدالـة π(س) = عدد الأعداد الأولية ب التي تحقق العلاقة س £ ب £ 2.
وقد لاحظ كل من العالمين لوجاندرA.M.Legendre ت(1752- 1833 م) وغوص C.F.Gauss ت(1777- 1855م)، كـل على حـده، أن نسـبة الـدالـة π(س) إلى الدالة س/لع س تقترب من الواحد في حال القيم الكبيرة لـ س، ولم يفلح أيّ منهما في إثبات وجود نهاية لهذه النسبة.
وفي عام 1851م أثبت العالم الروسي تشيبيتشيف P.L.Tchebychev ت(1821-1894 م ) أنّه إن كان لهذه النسبة نهاية فهذه النهاية تساوي 1.
وفي عام 1896م أفلح كلُّ من بوسان C.J.V.Poussin وآدامار G.Hadamard من إثبات وجود هذه النهاية، وفي عام 1949م نشر سلبرغ Selberg برهاناً بسيطاً أثار ضجة علمية.
من القضايا المثيرة في نظرية الأعداد تخمين غولد باخC.Goldbach ت(1690- 1764م) الذي خمّن فيه أنّ كل عدد زوجي £ 4 هو مجموع عددين أوليين. وقد جربت الأعداد حتى العدد 33 × 10 ووجد أنّ كل عدد زوجي £ 6 هو مجموع عددين أوليين فرديين مختلفين.
وفي عام 1948م أثبت الرياضي رينيه A.Renye وجود عدد ب بحيث إنّ أي عدد صحيح زوجي كبير ن يمكن أن يكتب كمجموع عدد أولي وعدد آخر عدد عوامله الأولية لايتجاوز ب.
وفي عام 1966م أثبت العالم تشين غين ران Chen Ging-Run أنّ العدد ب ³ 2. ويمكن القول إن نظرية الأعداد ما زالت تحوي المئات من المسائل المفتوحة، وأن عدد المسائل الجديدة التي ليس لها حل أكثر من عدد المسائل المفتوحة التي يعثر لها على حل.
إن موضوع نظرية الأعداد هو العدد الطبيعي. فما هي مجموعة الأعداد الطبيعية ؟
لقد نشر جيوسيبي بيانو Giusepp Peano ت(1858-1932م) مقالةً عام 1889م أعطى فيها مفهوم مجموعة الأعداد الطبيعية (الأعداد الصحيحة غير السالبة) وفق مسلَّمات سميت مسلَّمات بيانو.
بعض كبار علماء الحساب
1- أبو علي الحسن بن الحسن بن الهيثم، ولد سنة 354 هـ/965م في البصرة، وتوفي في القاهرة سنة 432هـ/ 1041م. وقد ترك عدداً كبيراً من الكتب والمقالات في معظم فروع العلوم وفي الطب، ترجم الكثير منها إلى لغات أجنبية متعددة. ووجد لابن الهيثم 66 عملاً رياضياً تميزت بالمنهجية العلمية. ومن أهم ما صنف في علم الحساب كتاب: «في حل شكوك كتاب إقليدس في الأصول وشرح معانيه»، وقدم في هذا الكتاب براهين فاق الكثير منها البراهين التي قدمها إقليدس وحلّ الشكوك حول بعض مسائل إقليدس وشرحها.
2- جمشيد بن مسعود الملقب بغياث الدين الكاشي: ولد في المدينة الإيرانية كاشان، وورد أنه توفي نحو 845هـ/1436م. لم يكن الكاشي رياضياً فحسب بل كان فلكياً وطبيباً. وهو أول من تسلم إدارة مرصد ألوغ بك في سمرقند. للكاشي مؤلفات كثيرة في علوم رياضية متنوعة، آخر مؤلفاته رسالة «مفتاح الحساب» التي أنجزها في سمرقند سنة 1427م، وتعد هذه الرسالة موسوعة لرياضيات ذلك الزمان لما ورد فيها من مسائل مبتكرة تتعلق بأصول حساب الصحاح بالأرقام الهندية والحسابات التقريبية، وشرح للكسور العشرية. ثم إنه دوَّن في هذه الرسالة طريقة لاستخراج الجذور من أيّ دليل كان، وبحث في تحويل الأعداد الستينية إلى عشرية، وتكلم فيها على مراتب الأعداد (الخانات) وغير ذلك.
3- سنان بن الفتح الحراني (210هـ/825م)، كان رياضياً من أشهر مؤلفاته كتاب «الجمع والتفريق». وقد شرح فيه الطريقة التي يمكن أن تحل بها المسائل القائمة على الضرب والقسمة بالجمع والطرح.
ألف أيضاً كتاب «المكعبات»، شرح فيه طريقة توزيع الأعداد وتصنيفها، إضافة إلى جذورها وحساب مكعباتها.
4- تشيبيتشيف P.L.Tchebychev ت(1821–1894م): هو العالم الروسي الشهير الذي برع في نظرية الأعداد والتحليل والاحتمالات والميكانيك.
دعد الحسيني